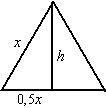© h.hofstede (h.hofstede@hogeland.nl)

1. a. zie de figuur hiernaast.
(1/2x)2 + h2 = x2
h2 = x2 - 1/4x2 = 3/4x2
h = √(3/4x2) = 1/2x√3

Dan is de oppervlakte van het grondvlak  1/2 • x • h =  1/4x2√3
Stel de hoogte van het prisma gelijk aan H, dan is de inhoud 
I =  1/4√3 • x2• H
 

    De totale lengte is 120 en dat is 6x + 3H, dus  6x + 3H = 120
3H = 120 - 6x 
H = 40 - 2x

en dat kun je invullen in de inhoudsformule:

 I = 1/4√3 • x2 • (40 - 2x) =  √3 • x2 • (10 - 1/2x)
       
  b. I = x2 • 10√3 - x3 • 1/2√3
I ' = 2x • 10√3  - 3 • 1/2√3x2 = 20√3 • x - 11/2√3 • x2
I ' = 0  geeft dan   x√3(20 - 11/2• x) = 0
x = 0  ∨  20 - 11/2x = 0
x = 0   ∨   x = 131/3
x = 131/3  geeft  I = 1026,4 cm3 
       
2. a. vul 2 punten in, bijv (2, 8.11)  en  (18, 35.49)
dat geeft  8,11 = 8 + a • 2b  en  35,49 = 8 + a • 18b
0,11 = a • 2b  en   27,49 = a • 18b
Die nu de tweede gedeeld door de eerste:   27,49/0,11 = 9b
9b = 250 ⇒  b = 2,51
0,11 = a • 22,51  geeft dan a ≈ 0,02 
       
  b. 5 km lopen met snelheid v km/uur kost  5/v uur
8 + 0,02 • v2,6 ademhalingen per minuut is 480 + 1.2 • v2,6  ademhalingen per uur.
In  5/v uur doe je dus  5/v • (480 + 1,2 • v2,6 ) = 2400/v + 6 • v1,6  ademhalingen.
Elke ademhaling is 0,2 liter, dus dat is  480/v + 1,2 • v1,6  liter lucht.
       
  c L ' = 0 voor het minimum;
-480 • v-2 + 1,2 • 1,6 • v0,6 = 0
vermenigvuldig alles met v2:   -480 + 1,92 • v2,6 = 0
1,92 • v2,6 = 480
v2,6 = 250
v = 2501/2,6 = 8,36  km/uur
       
3. a. Noem de lengte L (en de breedte x)
Dan geldt  2L + 4x = 500
2L = 500 - 4x
L = 250 - 2x

O = L • x = (250 - 2x) • x = 250x - 2x2 
       
  b. O ' = 0
250 - 4x = 0
x = 62,5
O = 250x - 2x2  = 7812,5 m2
       
4. a. Noem de breedte van de omheining B, dan geldt als je de omheining volgt:  x + B + x + 12 + B = 80
2x + 2B = 68
x + B = 34
B = 34 - x

O = (x + 12) • B = (x + 12)(34 - x) = 34x - x2 + 408 - 12x = 22x - x2 + 408
       
  b. O ' = 0
22 - 2x = 0
x = 11
O =  22x - x2 + 408 = 529 m2
       
  c. Met omheininglengte L  geldt: (zie uitwerking a)
x + B + x + 12 + B = L
2x + 2B = L - 12
x + B = 0,5L - 6
B = 0,5L - 6 - x
O = (x + 12) • B = (x + 12)(0,5L - 6 - x) = 0,5Lx - 6x - x2 + 6L - 72 - 12x
O ' = 0,5L - 6 - 2x - 12
Dat moet nul worden voor x = 8
0 = 0,5L - 6 - 16 - 12
0,5L = 34
L = 68 m 
       
5. a. noem de hoogte van de cilinder h
twee cirkels hebben lengte 4πr, en de vier opstaande ribben 4h
dus  4πr + 4h = 100
4h = 100 - 4πr
h = 25 - πr

De inhoud is  I = πr2 h  = πr2 • (25 - πr) = 25πr2 - π2r3
       
  b. I ' = 0
50πr - 3π2r2 = 0
πr(50 - 3πr) = 0
πr = 0  ∨  50 - 3πr = 0
r = 0  ∨  r = 50/3π

r = 50/3π  geeft  Imax = 736,8
       
  c. met n ribben  (zie uitwerking a):
twee cirkels hebben lengte 4πr, en de vier opstaande ribben nh
dus  4πr + nh = 100
nh = 100 - 4πr
h = 100/n - 4πr/n

De inhoud is  I = πr2 h  = πr2 • (100/n - 4πr/n) = 1/n(25πr2 - π2r3)
I ' = 0  geeft dan  1/n •(50pr - 3π2r2) = 0
50pr - 3π2r2 = 0 en dat heeft dezelfde oplossing als in vraag b)
       
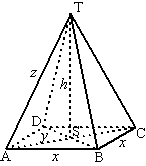
6. a. zie de figuur hiernaast.
AC2 = x2 + x2 = 2x2   AC = √(2x2) = √2 • x
Dan is  y = AS = 1/2√2 • x

z2 = h2 + y2 
⇒  h2 = z2 - y2 = z2 - (1/2√2x)2 = z2 - 1/2x2

totale lengte:  4z + 4x = 120  ⇒   z = 30 - x
h2 = (30 - x)2 + 1/2x2 = 900 - 60x + x2 - 1/2x2 = 900 - 60x + 1/2x2
h = √(900 - 60x + 1/2x2)

       
    I = 1/3 • x2 • h = 1/3x2 • √(900 - 60x + 1/2x2)  
       
  b. Y1 =  1/3 • X^2 • √(900 - 60X + 0,5X^2)
calc - maximum geeft dan  Imax =  821,29  (voor x = 13,94)		  
       
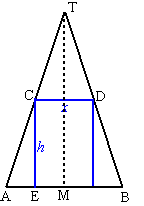
7. a. zie het vooraanzicht hiernaast.
de driehoeken AEC en AMT zijn gelijkvormig
AE/EC = AM/MT
AM = 4, MT = 12, EC = h,  AE = 4 - 0,5x

invullen:  (4 - 0,5x)/h = 4/12
12(4 - 0,5x) = 4h
48 - 6x = 4h
h = 12 - 1,5x

I = x2h = x2(12 - 1,5x) = 12x2 - 1,5x3   

       
  b. I ' = 0 ⇒  24x - 4,5x2 = 0
x(24 - 4,5x) = 0
x = 0 ∨  x = 51/3
Imax = 12 • (51/3)2 - 1,5 • (51/3)3  = 1137/9
Itotaal  = 1/3 • 82 • 12 = 256
dat is dan 1137/9 / 256 • 100% = 444/9%  
       
  c. de berekening gaat hetzelfde als in vraag a, met  r = 1/2x, dus  x = 2r
I = πr2h
= πr2h
= π • r2h
= π • r2 (12 - 1,5 • 2r)
= π • 12r2 - π • 3r3
       
  d. I ' = 24πr - 9πr2 = 0
πr (24 - 9r) = 0
πr = 0 ∨ 24 - 9r = 0
r = 0  ∨  r = 24/9 = 8/3
r = 8/3 geeft  I = 89,36
dat is  89,36/256 • 100% = 34,9%
       
8. Noem de hoogte van het schuurtje h, dan zijn de kosten:

voor- en achterkant:  2 • 1,5x • h • 150 = 450xh
links en rechts:  2 • x • h • 150 = 300xh
bovenkant:  1,5x • x • 250 = 375x2

samen is dat  K = 450xh + 300xh + 375x2  =  750xh + 375x2

de inhoud moet 60 zijn:  1,5x • x • h = 60 ⇒   h = 40/x2        

invullen in de kostenformule:   K = 750x • 40/x2  + 375x2  = 30000/x + 375x2 = 30000x-1 + 375x2

K' = -30000x-2 + 750x = 0
vermenigvuldig met x2 :  -30000 + 750x3 = 0
x3 = 30000/750 = 40
x = 401/3 = 3,42
Dan is K = 30000/x + 375x2 = €13158,-
       
9. a. Noem de hoogte van het doosje h dan geldt voor de kosten:

vier zijkanten:  4 • x • h • 0,005 = 0,02xh:
deksel:  0,008x2
bodem:  0,005x2

samen is dat  K = 0,013x2 + 0,02xh

inhoud:  x2h = 8000  ⇒  h = 8000/x2
invullen in de kostenformule:  K = 0,013x2 + 0,02x • 8000/x2 = 0,013x2  + 160/x
       
  b. K = 0,013x2  + 160/x = 0,013x2 + 160x-1
K ' = 0,026x - 160x-2 = 0
vermenigvuldig met x2:    0,026x3 - 160 = 0
0,026x3 = 160
x3 = 6153,85
x = 18,325

K = 0,013x2  + 160/x = €13,10
       
10. a. noem de hoogte van het potje h
de kosten zijn;
glazen bodem:  πr2 • 0,02
glazen zijkant:  2πr • 0,02 • h
metalen bovenkant:  πr2 • 0,05
metalen zijkant:  2πr • 2 • 0,05

totaal:  K = 0,02πr + 0,05πr2 + 0,04πrh + 0,2πr  =  0,07πr2 + 0,04πrh + 0,2πr

inhoud:  I = πr2h = 1000  dus  h = 1000/πr2
dat geeft:
K = 0,07πr2 + 0,04πr • 1000/πr2  + 0,2πr
K = 0,07πr2 + 40/r + 0,2πr
       
  b. Y1 = 0,07πX2 + 40/X + 0,2πX
calc - minimum geeft  minimale kosten K = 16,03  (voor r = 4,07)
       
11. Noem de straal van het grondvlak r
De kosten zijn dan:
boven- plus onderkant:  2 • πr2 • 0,004 = 0,008πr2
de mantel:  2πrh •  0,004 = 0,008πrh
de naden:  (h + 2 • 2πr) • 0,008 = 0,008h + 0,032πr

samen is dat K = 0,008πr2 + 0,008πrh + 0,008h + 0,032πr    

de inhoud is  1000:   πr2h = 1000 ⇒  h = 1000/πr2 
dat geeft  K = 0,008πr2 + 0,008πr • 1000/πr2  + 0,008 • 1000/πr2  + 0,032πr    
K = 0,008πr2 +  8/r  + 8/πr2 + 0,032πr

Y1 = 0,008πX^2 +  8/X  + 8/(πX^2) + 0,032πX
calc - minimum  geeft dan minimale kosten  €2,83  (voor r = 5,04)
       
12. a. Een vierkant is de figuur die bij een gegeven omtrek de grootste oppervlakte heeft.
       
  b. Noem de zijden van het vierkant x en de lengte L.
I = x2L

omtrek:  L + 4x = 250  dus  L = 250 - 4x
Dan is  I = x2(250 - 4x) = 250x2 - 4x3

I ' = 500x - 12x2 = 0
x(500 - 12x) = 0
x = 0   ∨   x = 500/12  = 412/3.
I = 250x2 - 4x3  = 144676
       
  c. Noem de straal van het grondvlak r en de lengte L
I = πr2 L

omtrek:  L + 2πr = 250  dus  L = 250 - 2πr
Dan is  I = πr2(250 - 2πr) = 250πr2 - 2π2r3 

I ' = 500πr - 6π2r2 = 0
r(500π - 6π2r) = 0
r = 0 ∨  r = 500/6π =  26,53
I = 250πr2 - 2π2r3  = 184207
       
13. a. Noem M het midden van AB.
de driehoeken CMA en PQA zijn gelijkvormig
CM/MA = PQ/QA
10/6 = PQ/x
PQ = 5/3x

QR = AB - 2x = 12 - 2x

oppervlakte is O = PQ · QR = 5/3x(12 - 2x) = 20x - 10/3x2
       
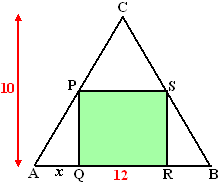  b. O ' = 20 - 20/3x = 0
x = 3
O = 20x - 10/3x2 = 30		  
       
  c. Met hoogte H geeft dezelfde berekening als in vraag a:
H/6 = PQ/x
PQ = Hx/6

oppervlakte is  O = Hx/6 (12 - 2x) = 2Hx - 1/3Hx2
O '=  2H - 16x - 2/3xH = 0
x = 3
Dan is QR = 12 - 6 = 6
dus moet PQ ook 6 zijn, anders is het geen vierkant:   Hx/6 = 3H/6 = 6
H = 12 
       
14. a. maïs is  x2
koolzaad is  (400 - x)2 = 160000 - 800x + x2
dan blijft over:  400 · 300 - x2 - 160000 + 800x - x2 =  800x - 40000 - 2x2
       
  b. O ´ = 800 - 4x = 0
x = 200
Dus de maïs  200 bij 200 en het koolzaad ook.
       
15. a. Stel dat de balk x bij x bij h is.
Kosten:
   links, rechts en voor:  3· xh · 50 = 150xh
   boven:  80x2
    bodem:  30x2 
In totaal  K = 150xh + 110x2 
inhoud:  x2h = 30  dus  h = 30/x2
dan is  K = 150x(30/x2) + 110x2 = 4500/x + 110x2 

Prisma:  stel de bodem x bij x en de hoogte van het voorvlak h
zie het zijaanzicht hiernaast.
dan is de hoogte langs de muur x + h  (vanwege de 45º) en dan is de schuine zijde x√2
Kosten:
   links en rechts:  2 • (xh + 1/2x2) • 50 = 100xh + 50x2
   voor: 50xh
   boven:  x • x√2 • 80
   onder:  30x2 
In totaal  K = 100xh + 50x2 + 50xh + 80x2√2 + 30x2
K = 150xh + 80x2 + 80x2√2

De inhoud is  (xh + 1/2x2) • x = x2h + 1/2x3 = 30
x2h = 30 - 1/2x3
h = 30/x2 - 1/2x  en dat kun je in de K-formule invullen:
K = 150x • (30/x2 - 1/2x) + 80x2 + 80x2√2
K = 4500/x - 75x2 + 80x2 + 80x2√2
K = 4500/x - 5x2  + 80x2√2

       
  b. Balk:   K =   4500/x + 110x2  = 4500x-1 + 110x2
K' =  -4500x-2 + 220x = 0
vermenigvuldig met x2 :  -4500 + 220x3 = 0
x3 = 4500/220 = 20,45
x = 20,451/3 = 2,73
K =    4500/x + 110x2   = 2468,16

Prisma:   4500/x - 5x2  + 80x2√2  = 4500x-1 + 110x2 + 80x2√2
K '  =  -4500x-2 + 220x + 160x√2 = 0
vermenigvuldig met x2 :   -4500 + 220x3 + 160x3√2 = 0
x3 • (220 + 160√2) = 4500
x3 = 10,08
x = 2,16
K = 4500/x - 5x2  + 80x2√2 = 2587,78
       
16. Noem de breedte van het kastje B en de hoogte h
Dan geldt  voor de inhoud  I = 50Bh

Maar de totale lengte is:   3B + 4h = 600
h = 150 - 0,75B
Dan is  I = 50B(150 - 0,75B) = 7500B - 37,5B2

I ' =  7500 - 75B = 0
B = 100

I = 7500B - 37,5B2  = 375000 cm3
       
17. Noem de straal van het grondvlak van het  badje r, dan is de hoogte h = 6 - r
inhoud  I = πr2h = πr2 (6 - r) = 6πr2 - πr3 
I ' = 12πr - 3πr2 = 0
 πr(12 - 3r) = 0
r = 0   ∨  r  = 4 

r = 4 geeft  I =  6πr2 - πr3  =  32π  = 100,53
       
18. Met w glazen wijn en s sigaren geldt:  100 = 3w + 2s  dus  s = 50 - 1,5w

G = w2 • s = w2(50 - 1,5w) = 50w2 - 1,5w3

G ´  = 90w - 4,5w2  = 0
w(90 - 4,5w) = 0
w = 0  ∨  w = 90/4,5  = 20    

w = 20  geeft  s = 50 - 1,5w = 20
Hij moet 20 sigaren en 20 glazen wijn nemen.
       
19. Noem de lengte van het stuk land L en de totale lengte van het gaas  G
Dan geldt:

L + 3x = G  ⇒  L = G - 3x
oppervlakte:  O = xL = x(G - 3x) = xG - 3x2

O ' = G - 6x
Dat is nul als x = 100, dus G = 600  
       
20. a. Oppervlakte 30 betekent BL = 30  ⇒  B = 30/L 
   
     
       
  b. K = 21271L-1 + 232,6L
K ' = -21271L-2 + 232,6 = 0
vermenigvuldig met L2:   -21271 + 232,6L2 = 0
232,6L2 = 21271
L2 = 91,45
L = 9,56  en dan is B = 30/L = 3,14
       
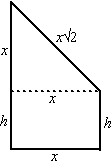
21. a. Zie de figuur hiernaast.
b + 2x = 80  dus  x = 40 - 0,5b
sin30˚ = 0,5 = y/x  dus y = 0,5x = 20 - 0,25b
cos30˚ = 1/2√3 = h/x  dus  h = 1/2√3x = 1/2√3(40 - 0,5b)  

oppervlakte:  O = hb + hy
O = 1/2√3(40 - 0,5b)b + 1/2√3(40 - 0,5b)(20 - 0,25b)
O = 1/2√3{40b - 0,5b2 + 800 - 10b - 10b + 0,125b2 }
O = 1/2√3(-0,375b2 + 20b + 800)
O = √3(-0,1875b2 + 10b + 400)
       
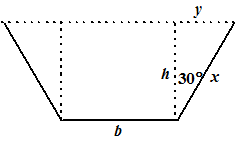  b. O ' = √3(-0,375b + 10) = 0
b  = 10/0,375 = 262/3
O = √3(-0,1875b2 + 10b + 400) = 923,76
       
22. Teken de diameter door de doorsnede van de balk.
Dan geldt:  (2r)2 = x2 + y2  dus  y2 = 4r2 - x2 = 324 - x2

D = 3xy2 = 3x(324 - x2) = 972x - 3x3
D ' = 972 - 9x2  = 0
9x2 = 972
x2 = 108
x = 10,39 en dan is  y2 = 324 - x2 = 216  dus  y = 14,70
       
23. noem de zijden van de driehoek x, dan is de lengte voor het vierkant  2 - 3x dus zijn de zijden van het vierkant
1/4(2 - 3x) = 0,5 - 0,75x

De oppervlakte van het vierkant is  (0,5 - 0,75x)2   = 0,25 - 0,75x + 0,5625x2
 
  Noem de hoogte van de driehoek h, dan geldt:
h2 + (0,5x)2 = x2
h2 = x2 - 0,25x2
h2 = 0,75x2
h = x√(0,75)

de oppervlakte is dan   0,5 · x · x√(0,75) = 0,5x2√0,75
       
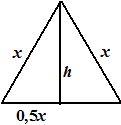  oppervlakte driehoek plus vierkant:  O = 0,25 - 0,75x + 0,5625x2  + 0,5x2√0,75

maximum:  O ' = -0,75 + 1,125x + x√0,75 = 0
x(1,125 + √0,75) = 0,75
x · 1,991 = 0,75
x =  0,377

Dan is O = 0,25 - 0,75x + 0,5625x2  + 0,5x2√0,75 = 0,1087 m2
       
24. a. De aankoopkosten van de grond per hectare zijn ƒ170.000,-. Als er x woningen op gebouwd worden is dat per woning  170000/x in guldens ofwel  170/x = 170 • x -1 in duizenden guldens. Dat is KA
Den kosten voor het bouwrijp maken zijn  B = 0,4 • x1,8 dus per woning is dat  (0,4•x1,8)/x = 0,4 • x0,8
en dat is KB
       
  b. KA + KB = 170 • x-1 + 0,4 • x0,8
De afgeleide daarvan is  -1 • 170 • x-2 + 0,4 • 0,8 • x-0,2 = -170x-2 + 0,32x-0,2
Plot deze afgeleide en kijk wanneer hij nul is
Dat is bij x = 32,6629 
x is een aantal huizen en moet dus een geheel getal zijn.
x = 32 geeft  K = 11,7125
x = 33 geeft  K = 11,7110
Voor minimale kosten moet de gemeente dus 33 woningen per hectare bouwen.
In dat geval is  KA = 170 • 32-1 = 5,1515... en KB = 0,4 • 330,8 = 6,5595....
Die zijn dus niet gelijk.
       
25. a. 50 cm per dwarsbuis.
voor 10 dwarsbuizen is dan 500 cm nodig
dus voor de rechtopstaande buizen blijft 900 - 500 = 400 cm over
dat is 200 cm per stuk.
De hoogte is dus 200 cm.
       
  b. Volg de redenering van de vorige vraag:
b cm per dwarsbuis
voor 10 dwarsbuizen is dan  10b cm nodig
dus voor de rechtopstaande buizen is  900 - 10b cm over
dat is  450 - 5b per stuk.
Dus h = 450 - 5b

of:
de totale lengte is 2h + 10b en dat moet 900 zijn
2h + 10b = 900  geeft  2h = 900 - 10b  dus  h = 450 - 5b

of:
Als er een lineair verband is, dan geldt  h = a • b + c
Twee waarden die voldoen zijn bijv.  (b = 0 en h = 450)  en  (b = 50 en h = 200 (vraag 20))
a = Δh/Δb = (200 - 450)/(500 - 0) = -5
bij b = 0 is h = 450 dus c = beginwaarde = 450
Dat geeft  h = -5 • b + 450
       
  c. V' = -5 • 2 • b + 450 = -10b + 450
maximale V vinden we als V'= 0  dus  -10b + 450 = 0  ⇒  10b = 450  ⇒  b = 45
b = 45 geeft  V = -5 • 452 + 450 • 45 = 10125 cm2
       
26. a. De oppervlakte van een cilinder is  2πr2+ 2πrh = 2πr2 + 2πr · 8000/πr2  = 2πr2 + 16000/r
De inhoud is  πr2h
   
       
  b. F = 2r -1 + π/4000 • r2
F '= -2r -2 + 2π/4000 • r = 0
vermenigvuldig alles met r2 :  -2 + 2π/4000 • r3 = 0
⇒  2π/4000 • r3 = 2
⇒  0,00157 • r3 = 2
⇒  r3 = 1273,24
⇒  r = (1273,24)1/3 ≈ 10,8 cm
       
27. a. A(t,8) en B(8,0) dus Pythagoras geeft: 
AB = √((t - 8)2 + 82 )
= √(t2 - 16t + 64 + 64)
= √(t2 - 16t + 128)
       
  b. Een gelijkbenige driehoek met lange zijde t heeft rechthoekszijden 1/2√2•t
Een gelijkbenige driehoek met lange zijde 16 - t heeft rechthoekszijden 1/2√2• (16 - t)
De oppervlakte is dus 1/2√2• t • 1/2√2• (16 - t) = 1/4 • 2 • (16t - t2) = 8t - 1/2t2 
       
  c. G'(t) = -t + 8 en dat is nul als t = 8

a'(t) = 1/2(128 - 16t + t2 )-1/2 • (-16 + 2t) en dat is nul als -16 + 2t = 0  ofwel als t = 8.

Dat is dus tegelijk.
       
28. a. de zijden van de bodem zijn beiden  b - 2x en de hoogte is x
De inhoud is dan I = (b - 2x)2 x
I = (b - 2x)(b - 2x)x
I = (b2 - 2xb - 2bx + 4x2)x
I = b2x - 4x2b  + 4x3  
       
  b. I ' = b2 - 8xb + 12x2
x = 1/6b geeft  I ' = b2 - 8 · 1/6b2 + 12 (1/6)2b2
I ' = b2 - 8/6b2 + 12/36b2  = 0b2 = 0
Dat is dus een maximum.
       
29. a. De breedte is gelijk aan  (1 - 1/p)
De lengte is gelijk aan (3 - p)
(1 - 1/p) • (3 - p) = 1/2
3 - p - 3/p + 1 = 1/2
vermenigvuldig met p:   4p - p2 - 3 + p = 1/2p
p2 - 3,5p + 3 = 0
ABC formule geeft  p = 2  of  p = 1,5 
       
  b. Als de oppervlakte maximaal is moet de afgeleide nul zijn:
O = 4/3(-p + 4 - 3p-1 )  dus  O' = 4/3(-1 + 3/p2) = 0
dat geeft  3/p2 = 1 ⇒  p2 = 3  ⇒  p = √3.  (p = -√3 voldoet niet).
       
30. Als de zijde van A gelijk is aan x, dan is de zijde van B gelijk aan 30 - x
Dan is de zijde van C gelijk aan  20 - zijde van B = 20 - (30 - x) = x - 10
A + B + C =  x2 + (30 - x)2 + (x - 10)2
D = 20 • 30 - A - B - C = 600 - x2 - (30 - x)2 - (x - 10)2
= 600 - x2 - (900 - 60x + x2) - (x2 - 20x + 100)
= 600 - x2 - 900 + 60x - x2  - x2 + 20x - 100
= -3x2 + 80x - 400
Dat is maximaal als de afgeleide ervan nul is:  -6x + 80 = 0 ⇒  x = 80/6 = 131/3  
       
31. a. de lange kant van het papier heeft lengte  2l + 2h
de smalle kant heeft lengte b + 2 • 0,5h = b + h
de oppervlakte is dan  (2l + 2h)(b + h) = 2lb + 2lh + 2hb + 2h2
       
  b. De inhoud is  I = l • b • h
b + h = 50 geeft  h = 50 - b
Dan is  I = l • b • (50 - b)

2l + 2h =120 ⇒   2l = 120 - 2h  ⇒  l = 60 - h
Maar omdat  h = 50 - b geeft dat  l = 60 - (50 - b) = 10 + b
Dan is  I = (10 + b) • b • (50 - b)    en dat is inderdaad de gegeven formule
       
  c. I = (10 + b) • b • (50 - b) = (10b + b2) • (50 - b) = 500b - 10b2 + 50b2 - b3 = 500b + 40b2 - b3
Voor het minimum is de afgeleide nul:  I ' = 500 + 80b - 3b2 = 0
ABC-formule:  b = (-80 ± √(12400)/-6  en dat is  31,89  (of  -5,22 maar die oplossing kan natuurlijk niet)
Dan is I = (10 + 31,89) • 31,89 • (50 - 31,89) = 24192,64.. ≈ 24193 cm3
       
32. a. ENT is gelijkvormig met PMT, dus  EN/TN = PM/TM
TN = x
TM = x + 1
EN is de helft van  EG en EG = √(12 + 12) = √2, dus  EN = 0,5√2.
Invullen in de verhoudingen geeft   0,5√2/x = PM/(x + 1) ⇒  0,5√2/x • (x + 1) = PM en dat is de gegeven formule.
       
  b. bedenk dat  (x + 1)/x = x/x + 1/x = 1 + 1/x, dan geldt:  
   
    = 1/6π • (1 + 2x-1 + x-2)(x + 1) =  1/6π •(x + 1 + 2 + 2x-1 + x-1 + x-2) = 1/6π • (3 + x + 3x-1 + x-2)
       
  c. I = 1/6π • (x + 3 + 3x-1 + x-2 )
Je vindt het minimum als de afgeleide nul is
I ' = 1/6π • (1 - 3x-2 - 2x-3) = 0
Y1 =  1 - 3*X^(-2) - 2 *X^(-3)  en dan calc - zero  geeft  x = 2
De inhoud is dan  I =  1/6π • (2 + 3 + 3 • 2-1 + 2-2 ) = 9/8π
       

© h.hofstede (h.hofstede@hogeland.nl)