|
|||||
| 1. | a. | f(x) = cos(3x)
f '(x) = -sin(3x) 3 = -3sin(3x) die 3 komt van de kettingregel. |
|||
| b. | y = 2sinx + cos(x2) y '= 2cosx - sin(x2) 2x = 2cosx - 2xsin(x2) die 2x komt van de kettingregel. |
||||
| c. | f(x) = sin(x + 3) -
2cos(5 - x) f '(x) = cos(x + 3) - 2 -sin(5 - x) -1 = cos(x + 3) - 2sin(5 - x) |
||||
| d. | f(x) =
√(cosx)
= (cosx)0,5 f '(x) = 0,5 (cosx)-0,5 -sinx = -sinx/2√(cosx) |
||||
| e. | y = 5 - 2cos(2πx
- 3) y ' = - 2 -sin(2πx - 3) 2π = 5 + 4πsin(2πx - 3) |
||||
| f. | f(x) = sin2(x)
= (sinx)2 f '(x) = 2 sinx cosx die cos x komt van de kettingregel. |
||||
| g. | y = 2 - sin(x2 + 3) y '= -cos(x2 + 3) 2x = -2xcos(x2 + 3) die 2x komt van de kettingregel. |
||||
| h. | y = 4cosx sinx y' = 4 -sinx sinx + 4cosx cosx = -4sin2x + 4cos2x met de productregel. |
||||
| 2. | Met de quotiλntregel: | ||||
|
|
|||||
| Als je gebruikt dat
cos2x + sin2x = 1 dan geeft dat de
afgeleide 1/cos2x Als de de breuk uitdeelt geeft dat de afgeleide 1 + sin2x/cos2x = 1 + tan2x |
|||||
| 3. | a. | √(6sinx)
= -2cosx 6sinx = 4cos2x 6sinx = 4(1 - sin2x) 6sinx = 4 - 4sin2x 4sin2x + 6sinx - 4 = 0 noem nu sinx = p 4p2 + 6p - 4 = 0 ABC-formule: p = (-6 ±√(36 + 64))/8 = (-6 ± 10)/8 = 1/2 of -2 sinx = -2 kan niet, dus blijft over sinx = 1/2 x = 1/6π + k2π ∨ x = 5/6π + k2π controleren (want we hebben gekwadrateerd): alleen x = 5/6π is een goede oplossing. |
|||
| b. | Als de grafieken
elkaar loodrecht snijden dan moet gelden f ' g' =
-1 f '(x) = 0,5 (6sinx)-0,5 6cosx f '(5/6π) = 0,5 3-0,5 6 -1/2√3 = -11/2 g '(x) = -2 -sinx = 2sinx g'(5/6π) = 2 1/2 = 1 f ' g ' is niet gelijk aan -1, dus de grafieken snijden elkaar niet loodrecht. |
||||
| 4. |
|
||||
| dat is nul als de
teller nul is: 6cosx - 3cos2x - 3sin2x = 0 6cosx - 3(cos2x + sin2x) = 0 6cosx - 3 = 0 6cosx = 3 cosx = 1/2 x = 1/3π ∨ x = 12/3π x = 1/3π geeft y = 3 1/2√3 / (2 - 1/2) = 3√3 en de top (1/3π, 3√3) x = 12/3π geeft y = 3 -1/2√3 / (2 - 1/2) = -3√3 en de top (12/3π, -3√3) |
|||||
| 5. |
|
||||
|
|
|||||
| 6. | a. | De functie bestaat niet als 1 + sinx = 0 dus bij x = 11/2π. | |||
|
|
|||||
| Dat is nul als de
teller nul is: sinxcosx(2 + sinx) = 0 sinx = 0 ∨ cosx = 0 ∨ 2 + sinx = 0 maar dat laatste kan niet. x = 0 ∨ x = π ∨ x = 2π ∨ x = 1/2π ∨ x = 11/2π en die laatste valt af, omdat de functie daar niet bestaat. Dat geeft de punten (0, 0) en (π, 0) en (2π, 0) en (11/2π, 1/2) |
|||||
| b. | sin²x/(1
+ sinx) = 1/6 sin2x = 1/6 (1 + sinx) 6sin2x = 1 + sinx 6sin2x - sinx - 1 = 0 noem nu sinx = p 6p2 - p - 1 = 0 ABC-formule: p = (1 ±√(1 + 24))/12 = (1 ± 5)/12 = 1/2 of -1/3 sinx = 1/2 ∨ sinx = -1/3 x = 1/6π ∨ x = 5/6π ∨ x = sin-1(-1/3) = -0,34 ∨ x = π - - 0,34 = 3,48 |
||||
| c. | Als ze elkaar raken
moet gelden f = g en f ' = g'
Eerst maar de afgeleides gelijkstellen: sinxcosx(2 + sinx)/(1 + sinx)2 = -3cosx Ga nu delen door cosx en vermenigvuldigen met de noemer: sinx(2 + sinx) = -3(1 + sinx)2 ∨ cosx = 0 2sinx + sin2x = -3(1 + 2sinx + sin2x) ∨ cosx = 0 2sinx + sin2x = -3 - 6sinx - 3sin2x ∨ cosx = 0 4sin2x + 8sinx + 3 = 0 ∨ cosx = 0 ABC-formule: sinx = (-8 ±√(64 - 48))/8 = (-8 + 4)/8 = -11/2 of -1/2, ∨ cosx = 0 x = 11/6π ∨ x = 15/6π ∨ x = 1/2π ∨ x = 11/2π Verder moet ook nog gelden f = g x = 11/6π: (1/4)/(1 - 1/2) = p - 3 -1/2 ⇒ 1/2 = p + 11/2 ⇒ p = -1 x = 15/6π: zelfde resultaat x = 1/2π: 1/(1 + 1) = p - 3 1 ⇒ 1/2 = p - 3 ⇒ p = 31/2 x = 11/2π geeft geen oplossing want dan bestaat f niet. |
||||
| 7. | Bekijk alleen het
gebied x in [0, 2π] want dat is de
periode van de functie. Nulpunten: 2cosx - a = 0 ⇒ 2cosx = a ⇒ cosx = 1/2a (Verder mag sinx niet nul zijn, dus x mag niet 0, π, 2π zijn) Dat heeft oplossingen als -2 < a < 2 Extremen: f ' = 0 |
||||
|
|
|||||
| -2sin2x
- 2cos2x + acosx = 0 -2(sin2x + cos2x) + acosx = 0 -2 + acosx = 0 acosx = 2 cosx = 2/a Dat heeft oplossingen als a > 2 of a < -2 Er zijn inderdaad geen waarden van a waarvoor beide voorwaarden kloppen. |
|||||
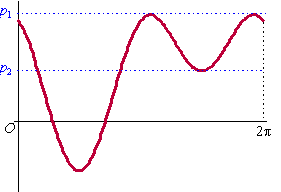
| 8. | a. | Zie de figuur hiernaast. Er zijn 4 snijpunten als p tussen de lijnen p1 en p2 in ligt. Het is dus zaak de plaats van de maxima en minima van f te vinden. f '(x) = -2sin(2x) - cosx = 0 -2 2sinxcosx - cosx = 0 cosx(-4sinx - 1) = 0 cosx = 0 ∨ sinx = -1/4 x = 1/2π ∨ x = 11/2π ∨ x = sin-1(-1/4) = -0,25 ∨ x = π - - 0,25 = 3,39 Dat geeft minima (1/2π, -1) en (11/2π, 1) Dat geeft maxima (3.39, 2.125) en (6.03, 2.125) |
 |
||
| Er zijn 4 snijpunten
voor 1 < p < 2,125 NB: De 2,125 is exact en niet afgerond. Als sinx = -1/4 dan is cos2x = 1 - 2sin2x = 1 - 2 1/16 = 7/8 Dan is f(x) = 7/8 - - 1/4 + 1 = 21/8. |
|||||
| b. | f '(p)
= -2sin(2
π) - cosπ
= 1 dus de raaklijn is y = x + b Die moet door (π, 2) gaan, dus 2 = π + b ⇒ b = 2 - π De raaklijn is dan y = x + 2 - π |
||||
| 9. | a. | f(x) =
2·cos x + sin2x + 1 f '(x) = -2sinx + 2cos(2x) = 0 -2sinx + 2(1 - 2sin2x) = 0 -2sinx + 2 - 4sin2x = 0 -2sin2x - sinx + 1 = 0 ABC-formule: sinx = (1 ±√(1 + 8))/-4 = (1 ± 3)/-4 = -1 of 1/2 sinx = -1 sinx = 1/2 x = 11/2π ∨ x = 1/6π ∨ x = 5/6π x = 1/6π geeft y = 2 1/2√3 + 1/2√3 + 1 = 1 + 11/2√3 en dat is het maximum x = 5/6π geeft y = 2 -1/2√3 - 1/2√3 + 1 = 1 - 11/2√3 en dat is het minimum |
|||
| b. | x = 11/2π geeft y = 2 0 + 0 + 1 = 0 dus dat is het punt ( 11/2π, 1) | ||||
| 10. | a. | De
afstand AB is de periode van de formule. Dat is 2π/(2π/p) Dus moet gelden p ≥ 8,00 |
|||
| b. | De helling is de afgeleide, en die mag dus maximaal 1/15 zijn. | ||||
|
|
|||||
| Dat is
een sinusoοde met amplitude -0,80π/p
dus moet gelden 0,80π/p
< 1/15 15 0,80π ≤ p (kruislings vermenigvuldigen) p ≥ 12π |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||