|
|||||
| 1. | a. |
1 + 2log(x -3)
= 6 2log(x - 3) = 5 x - 3 = 25 x - 3 = 32 x = 35 uit de grafiek lees je af dat g(x) < 6 geldt voor 〈3, 35〉 |
|||
| b. |
g(x) =
1 + 2log(x -3) = 2log2 + 2log(x - 3) = 2log(2(x - 3)) = 2log(2x - 6) dus a = 6 |
||||
| c. | plot Y1 = log(X)/log2
en Y2 = 1 + log(X - 3)/log(2) Y3 = 1 Y4 = Y1 - Y2 calc - intersect geeft als snijpunt van Y4 en Y3 de waarde x = 4 |
||||
| d. | f '(x) = 1/xln2 = 1/x • 1/ln2 = 1/x • 1,442695 | ||||
| 2. | a. | v1 = 20 km/uur
(10 km in 30 minuten) s1 = 10000 s2 = 400 invullen: v2 = 20 - 2log(400/10000) = 20 - 2log(0,04) = 20 - log(0,04)/log(2) = 20 - - 4,64 = 25 km/uur |
|||
| b. | als s2 groter
dan s1 is, dan is s2/s1
groter dan 1, en dan is 2log(s2/s1)
positief. dus is dan v2 kleiner dan v1 (je trekt een positief getal van v1 af) |
||||
| c. | s2 = 2s1
geeft s2/s1
= 2 en 2log(s2/s1)
= 2log2 = 1 dan is v2 = v1 - 1 een verdubbeling van de afstand betekent een verlaging van 1 km/uur |
||||
| d. |
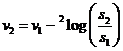 |
||||
| v2 - v1
= 2log(s2/s1) 2v2 - v1 = s2/s1 s2 = s1 • 2v2 - v1 |
|||||
| 3. | Als je
de grafiek van y = 2lnx een afstand a naar links
verschuift krijg je de grafiek van y = 2ln(x + a) P: y = 0 2ln(x + a) = 0 ln(x + a) = 0 x + a = 1 x = 1 - a Q: x = 0 y = 2lna -OP = OQ geeft dan 1 - a = 2lna Y1 = -(1 - X) en Y1 = 2ln(X) en dan intersect geeft X = a = 1 en X = a = 3,513 De gezochte oplossing (want a > 1) is a = 3,51 |
||||
| 4. | a. | Voor een exponentieel
verband moet je ENKEL-logpapir gebruiken. De grafiek wordt dan (bij benadering) een rechte lijn. |
|||
| b. | P = B • gA
(750, 30000) geeft 30000 = B • g750 (1600, 9000) geeft 9000 = B • g1600 Op elkaar delen geeft 30000/9000 = g(750 - 1600) 3,333 = g-850 g = 3,333-1/850 = 0,99966 30000 = B • g750 geeft dan 30000 = B • 0,7758 dus B = 38668 De formule is P = 38668 • 0,99966A |
||||
| c. | Omzet = O = A
• P = A • 841 • 2-0,0139A Voor het maximum is de afgeleide nul: 841 • 2-0,0139A + A • 841 • 2-0,0139A • ln2 • -0,0139 = 0 841 • 2-0,0139A • (1 - A • 0,0139ln2) = 0 1 - A • 0,0139ln2 = 0 1 - 0,00963A = 0 A = 104 |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||