© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. f ' (x) = 6 + 4 • 1/x  =  6 + 4/x  
       
  b. f '(x) = 3 • 1/(2x + 4) • 2  = 6/(2x + 4)  
       
  c. f ' (x) = 3x2 - 2 • 1/x  = 3x2 - 2/x  
       
  d. f ' (x) = 1 • lnx + x • 1/x = lnx + 1  
       
  e.  
       
  f. f '(x) = 4 • (3 + lnx)3 • 1/x  
       
  g. f '(x) =  2 • lnx • 1/x  
       
  h. f '(x) = -1/x2 • 2x  = -2/x  
       
  i. f '(x) = 1/lnx • 1/x = 1/(xlnx)  
       
2. een lijn door de oorsprong is de lijn y = ax
de lijn raakt de grafiek van f als de functies gelijk zijn en hun afgeleide ook.		  
 
  dus:  ax = (4 + 2lnx)/x  en   a = (-2-2lnx)/x2  
vul de tweede vergelijking in in de eerste:
(-2-2lnx)/x2  • x = (4 + 2lnx)/x
(-2-2lnx)/x = (4 + 2lnx)/x
-2 - 2lnx = 4 + 2lnx
-6 = 4lnx
lnx = -1,5
x = e-1,5 = 1/e√e

Dan is  y = (4 - 2 • 1,5)/e-1,5 = e1,5  = e√e
       
3. Bij een horizontale raaklijn is de afgeleide nul.
 
  -1 - p + lnx = 0
p = -1 + lnx

y = (-1 + lnx - lnx)/x
y = -1/x
       
4. a.  
       
  b. de afgeleide van xlnx is (met de productregel) gelijk aan  1 • lnx + x • 1/x = lnx + 1
de afgeleide van exlnx  is dan (met de kettingregel)   exlnx • (lnx + 1)
omdat xx = exlnx   is de afgeleide dus  exlnx • (lnx + 1) = xx • (lnx + 1)
       
5. a.  
    dat is nul als  1 - lnx = 0  ⇒  lnx = 1 ⇒  x = e
dan is y = lnx/x = 1/e
de top is  (e, 1/e)  		 
       
  b.
    dat is nul als  1 - lnpx = 0 ⇒  lnpx = 1  ⇒  px = e  ⇒   p = e/x  
   
       
  c. Plotten met de GR:
Y1 = ln(kx)/x  en  Y2 = 1, en bereken via intersect beide snijpunten.
Voor k = 4 is het verschil daartussen meer dan 1.   (x = 2,15 en x = 0,36)
       
  d. Stel de x-coφrdinaat van punt A is  p
Als AB = 1 is de x-coφrdinaat van B gelijk aan p + 1.

Die moeten beiden y = 1 opleveren
punt A:  ln(kp)/p = 1  geeft  lnkp = p
punt B:  ln(k(p + 1))/(p + 1) = 1  geeft  ln(k(p + 1)) = p + 1
uit de eerste volgt  kp = ep   dus  k = ep/p
invullen in de tweede:
   
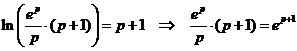    ep + ep • 1/p = ep • e
ep • (1 + 1/p - e) = 0
1 + 1/p - e = 0
1/p = e- 1
p = 1/(e - 1)		  
     
       
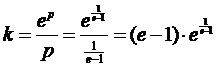6. ln(2 - x) = p  ⇒  2 - x = ep ⇒   x = 2 - ep
de helling is  1/(2-x) • -1  = -1/(2 - x) = -1/(2 - 2 + ep) = -1/ep  

1 + lnx = p ⇒  lnx = p - 1 ⇒  x = ep - 1 
de helling is  1/x = 1/ep - 1  
       
 
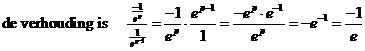  dat is inderdaad constant.
       
7. als ze raken zijn hun functiewaarden gelijk en ook de afgeleiden.
       
 
  g '(x) =  1/x
 
  x = (x - 2)2
x = x2 - 4x + 4
x2 - 5x + 4 = 0
(x - 4)(x - 1) = 0
x = 4  ∨   x = 1

Voor deze x-waarden moet dan ook nog de functiewaarden gelijk zijn:

x = 1 geeft:  f(1) = 0 en  g(1) = p  dus  p = 0

x = 4 geeft  f(4) = -1,5  en  g(4) = p + ln4   dus  p + ln4 = -1,5  ⇒   p = -1,5 - ln4
       
8.
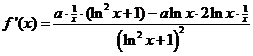  dat geeft  f '(1) =  (a - 0)/1 = a 
de raaklijn heeft vergelijking  y = a • x + b
f(1) = 0, dus moet gelden:  0 = a • 1 + b    b = -a
De raaklijn is de lijn  y = ax - a

snijpunt met de y -as:  x = 0 dus  y = -a  en het punt  (0, -a)
snijpunt met de x-as:  y = 0  dus  0 = ax - a ⇒  x = 1 en het punt  (1, 0)

De driehoek heeft een rechthoekszijde van a en eentje van 1, dus de oppervlakte is  0,5 • a • 1
0,5 • a • 1 = 2  
a = 4
De oppervlakte is kleiner dan 2 voor  0 < a < 4
       
9. a.  
    f ' = 0  geeft dan   2lnx - ln2x = 0
lnx(2 - lnx) = 0
lnx = 0 ∨  lnx = 2
x = 1   ∨   x = e2
x = 1 geeft  y = 0   en een minimum  (1, 0)
x = e2  geeft  y = 4/e2   en  een  maximum (e2 ,  4/e2)  		 
       
  b. f '(e3) =  (2 • 3 - 32)/e6 = -3/e6
de raaklijn is de lijn  y = -3/e6 • x + b

f(e3) = 9/e3  dus het raakpunt is  (e3, 9/e3)
9/e3 = -3/e6 • e3 + b
b = 12/e3
De raaklijn is de lijn   y = -3/e6 • x + 12/e3

punt P:  y = 0 :  0 = -3/e6 • x + 12/e3
3/e6 • x = 12/e3
x = 4e3

punt Q:  x = 0:  y = 12/e3

de oppervlakte is dan  1/2 • 12/e3 • 4e3 = 24		  
       
10. a.
       
  b. Als de grafiek de x-as raakt moet gelden  f(x) = 0  en  f '(x) = 0
f(x) = 0  geeft   2x - px = 0
f '(x) = 2xln2 - p = 0  geeft  p = 2xln2
de laatste invullen in de eerste:  2x - 2xln2• x = 0
2x(1 - xln2) = 0
xln2 = 1  (∨ 2x = 0  maar dat kan niet)
x = 1/ln2
p = 21/ln2 • ln2 = eln2		  
       
11. a. dan moet gelden
functies gelijk:  x = alnx
hellingen gelijk:  1 = a • 1/x
uit de tweede volgt  a = x en dat kun je dan invullen in de eerste:
x = xlnx
x - xlnx = 0
x(1 - lnx) = 0
x = 0  (maar dan bestaat lnx niet) ∨  x = e
dat geeft  a = e  
       
  b. 2lnx = ln(x + 6)
lnx2 = ln(x + 6)
x2 = x + 6
x2 - x - 6 = 0
(x - 3)(x + 2) = 0
x = 3  (∨ x = -2 maar dan bestaat lnx niet)
Het snijpunt is het punt  (3, 2ln3)

f 2'(x) =  2 • 1/x  dus  f2'(3) = 2/3 
de raaklijn aan de grafiek maakt een hoek met de x-as  waarvoor  geldt  tanα = 2/3  ⇒  α = 33,7Ί

g'(x) = 1/(x + 6)  dus  g'(3) = 1/9
de raaklijn aan de grafiek maakt een hoek met de x-as  waarvoor  geldt  tanα = 1/9 ⇒ α = 6,3Ί

de hoek tussen die raaklijnen (en dus tussen de grafieken) is dan  33,7 - 6,3 = 27,4Ί
       
12. a. f (x) = ln2x + 2lnx - 2
f '(x) = 2lnx • 1/x + 2 • 1/x  =  2lnx/x + 2/x = (2lnx + 2)/x
   
    dat is nul als  -2lnx = 0 ⇒  x = 1  en dan is  y = ln21 + 2ln1 - 2 = -2
Het buigpunt is het punt  (1, -2)

f '(1) = (2ln1 + 2)/1 = 2  dus de raaklijn is de lijn y = 2x + b
buigpunt invullen:  -2 = 2 • 1 + b  ή   b = -4

De buigraaklijn is de lijn y = 2x - 4 

       
  b. een lijn door O heeft vergelijking y = ax.
als zo'n lijn de grafiek raakt moeten de functies gelijk zijn ιn de afgeleiden ook.

afgeleiden gelijk:   a =  (2lnx + 2)/x
functies gelijk:  ax = ln2x + 2lnx - 2

Vul de eerste in in de tweede;
  (2lnx + 2)/x  • x  =  ln2x + 2lnx - 2
2lnx + 2 =  ln2x + 2lnx - 2
4 = ln2x
lnx = 2   ∨   lnx = -2
x = e2  ∨   x = e-2  en omdat   a =  (2lnx + 2)/x  kun je nu de bijbehorende a's uitrekenen
a = 6/e2 ∨   a = -2e2
De lijnen zijn dus  y = 6/e2 • x  en    y = -2e2 • x
       
13. f(x) =  x/lnx
 
 
  dat laatste is nul als  -1/x • ln2x + 2/x • lnx = 0
1/x • lnx • (-lnx + 2) = 0
1/x = 0  ∨  lnx = 0  ∨  lnx = 2
x = 1 ∨  x = e2
maar voor x = 1 bestaat de functie niet; dan is lnx = 0 en wordt er door nul gedeeld.
x = e2  geeft  y = 1/2e2  en het buigpunt is dus  (e2 , 1/2e2)

f '(e2) = (2 - 1)/22 = 1/4  dus de raaklijn is de lijn y = 1/4x + b
raakpunt invullen:  1/2e2 = 1/4e2 + b
b = 1/4e2
De buigraaklijn is de lijn  y = 1/4x +  1/4e2
       
14. f(p) = plnp
g(p) = p - 3

de grafiek van f ligt boven die van g dus de lengte van  PQ is   L =  plnp - (p - 3) =  plnp - p + 3
L is minimaal als de afgeleide ervan nul is.
L' = 1 • lnp + p • 1/p - 1 = 0
lnp = 0
p = 1

L = 1ln1 - 1 + 3 = 2 

       
15. a. 1/(xln2)  
       
  b. 1/(3xln3) • 3 = 1/(xln3)  
       
  c. 5 - 5/(xln5)  
       
  d. 1/(√xln4) • 1/2√x = 1/(2xln4)  
       
  e. 1/(xln4) + 1/(2xln4) • 2 = 1/xln4 + 1/xln4 = 2/xln4  
       
  f. xlog3 = log3/logx = log3 • (logx)-1
afgeleide:   log3 • -1 • (logx)-2 • 1/(xln10) =  -log3/(log2x • xln10)		  
       
16. a. L(7) = 53,4 + 1,1 • 7 + 1,4log 7
= 53,4 + 7,7 + log7/log1,4
= 66,9 cm		  
       
  b. L' (t) = 1,1 + 1/(tln1,4)
L'(6) = 1,1 + 1/(6ln1,4) = 1,6 cm/maand
       
  c. L ' = 2
1,1 + 1/(tln1,4)  = 2
1/(tln1,4) = 0,9
tln1,4 = 1/0,9 = 1,11
t = 1,11/ln1,4 = 3,3 maanden
       
17. a. 8 = alog(0 + b) - c • 0
8 = alogb
a8 = b
       
  b. N = 1,1log(t + 2) - 1,2t
N is maximaal als de afgeleide nul is;
N' = 1/(t + 2)•ln1,1 - 1,2 = 0
1/(t + 2)•ln1,1 = 1,2
(t + 2)ln1,1 = 1/1,2 = 0,8333
t + 2 = 0,8333/ln1,1 = 8,743
t = 6,743
N(6,743) = log(6,743 + 2)/log1,1 - 1,2 • 6,743 = 14,7
dat zijn 147 artikelen.
       
  c. N(0) =  1,1log(0 + 2) - 1,2 • 0 = 7,3
7,3 =  1,1log(t + 2) - 1,2t
Y1 =  log(X + 2)/log(1,1) -1,2X  en  Y2 = 7,3
intersect geeft  t = 21,5
dus na 21 ΰ 22 maanden.
       
18. a. 400 = 50 •  2log(x2 + 6)
8 = 2log(x2 + 6)
x2 + 6 = 28 = 265
x2 = 250
x = √250 = 15,8...
na 16 dagen zijn er voor het eerst meer dan 400 abonnementen
       
  b. A' = 50 • 1/(x2 + 6)ln2 • 2x 
A'(10) = 50 • 1/(102 + 6)ln2 • 20 = 13,6
dus 13 ΰ 14 abonnementen per dag. 

OF:
A(10) = 336
A(11) = 349
dat verandert met 13 per dag. 		 
       
  c. A' = 50 • 1/(x2 + 6)ln2 • 2x   moet maximaal zijn.
Y1 = 50 • 1/(x2 + 6)ln2 • 2x   en dan calc = maximum geeft  x = 2,45 dagen		  
       
19. h(x) = 1500 • log(5x + 1) - 100x
h'(x) = 1500 • 1/(5x + 1)ln10 • 5 - 100
h is maximaal als de afgeleide nul is.
1500 • 1/(5x + 1)ln10 • 5 - 100 = 0
7500 • 1/(5x + 1)ln10 = 100
 1/(5x + 1)ln10 = 1/75
(5x + 1)ln10 = 75
5x + 1 = 75/ln10
5x = 75/ln10 - 1
x = 15/ln10 - 1/5 = 6,3144
h = 1638 meter
     

© h.hofstede (h.hofstede@hogeland.nl)