|
|||||
| 1. | a. | ln4x = 2 4x = e2 x = 1/4e2 |
|||
| b. | ln(x + 6) = 2lnx ln(x + 6) = lnx2 x + 6 = x2 x2 - x - 6 = 0 (x - 3)(x + 2) = 0 x = 3 ∨ x = -2 x = -2 valt af, want daarvoor bestaat lnx niet. Dus blijft over x = 3 |
||||
| c. | ln(Φx) = lnx
+ 2 lnx0,5 - lnx = 2 0,5lnx - lnx = 2 -0,5lnx = 2 lnx = -4 x = e-4 |
||||
| d. | 3lnx = lnx + 2 3lnx - lnx = 2 2lnx = 2 lnx = 1 x = e |
||||
| e. | 2 ex = 6 ex = 3 x = ln3 |
||||
| f. | elnx = 3x
- 8 x = 3x - 8 8 = 2x x = 4 |
||||
| g. | 2 + lne2 = lnx 2 + 2 = lnx 4 = lnx x = e4 |
||||
| h. | lnx + ln2x = ln(x + 1) ln(x 2x) = ln(x + 1) 2x2 = x + 1 2x2 - x - 1 = 0 ABC formule geeft dan x = (1 ±√(1+8))/4 x = 1 ∨ x = -0,5 x = -0,5 valt af, want daarvoor bestaat ln2x niet. Dus blijft over x = 1 |
||||
| i. | ex - 1 = 4 x - 1 = ln4 x = 1 + ln4 |
||||
| j. | ln(1/x) = 3 + lnx ln(x-1) = 3 + lnx -lnx = 3 + lnx -2lnx = 3 lnx = -1,5 x = e-1,5 |
||||
| k. | ln(e2x + 1) = x
- 5 e2x + 1 = ex- 5 2x + 1 = x - 5 x = -6 |
||||
| l. | e2x + 2 =
3ex (ex)2 + 2 = 3ex (ex)2 - 3ex + 2 = 0 (ex - 2)(ex - 1) = 0 ex = 2 ∨ ex = 1 x = ln2 ∨ x = ln1 = 0 |
||||
| 2. | ln2x = p
geeft 2x = ep dus xA
= 1/2ep
lnx = p geeft xB = ep AB = xB - xA = ep - 1/2ep = 1/2ep xB = ep geeft yC = ln(2ep) = ln2 + lnep = ln2 + p BC = yC - yB = ln2 + p - p = ln2 De oppervlakte is dan 0,5 AB BC = 1/4ep ln2 4ln2 = 1/4ep ln2 16 = ep p = ln16 |
||||
| 3. | a. | f(x) = e2x
f '(x) = 2e2x f '(-1) = 2e-2 dus de raaklijn is y = 2e-2 x + b f(-1) = e-2 vul dat in inde raaklijn: e-2 = 2e-2 -1 + b e-2 = -2e-2 + b b = 3e-2 De raaklijn is y = 2e-2 x + 3e-2 |
|||
| b. |
|
||||
| Y1 = √(1 + e^(2X)) en dan calc - ∫f(x)dx en dan X = -2 en X = 3 geeft 10,01 | |||||
| c. | e2x =
p 2x = lnp x = 1/2lnp = ln(√p) 1 - e-x = p 1 - p = e-x ln(1 - p) = -x x = -ln(1 - p) AB = xB - xA = -ln(1 - p) - ln(√p) AB = -(ln(1 - p) + ln(√p)) AB = -ln((1 - p)√p) AB = -ln(√p - p√p) |
||||
| 4. | neem de logaritme ervan: | ||||
|
|
|||||
| Daaruit volgt a1/lna = e en dat is constant. | |||||
| 5. | a. | x = 0
geeft D = a en we kunnen aflezen dat dus moet gelden
a = 25000 Het tweede punt invullen: 10000 = 25000e-4b e-4b = 0,4 -4b = ln(0,4) = -0,9162.... Daaruit volgt b = -0,9162.../-4 = 0,22907... ofwel b = 0,23 |
|||
| b. | ln(D) = 10 - 0,2x dus
D = e10 - 0,2x = e10 e-0,2x
= 22026,46... e-0,2x en 22026,46... is bij benadering 22000 |
||||
| 6. | a. | Voor
de top geldt f '(x) = 0. Met de quotiλntregel: |
|||
| f '(x) = (8 ex - 8x ex)/(ex)2 | |||||
| Een
breuk is nul als de teller nul is: 8ex - 8x
ex = 0 ⇒ 8ex (1 - x) = 0 ⇒ x = 1 |
|||||
| b. | Snijden: 8x/ex
= 8nx/enx Kruislings vermenigvuldigen: enx 8x = ex 8nx enx 8x - ex 8nx = 0 8x(enx - nex) = 0 enx = nex enx/ex = n e(n - 1)x = n (n - 1)x = lnn x = 1/(n - 1) lnn |
||||
| 7. | J = 15, I = 2,5
geeft: 2,5 = 0,245 e1,488L + 0,0119 15 L 2,5/0,2345 = e1,488L + 0,1785L 10,66 = e1,6665L ln10,66 = 1,6665L 2,3665 = 1,6665L L = 1,42 meter |
||||
| 8. | a. | x e5x
= 3x x e5x - 3x = 0 x( e5x - 3) = 0 x = 0 of e5x = 3 De tweede oplossing geeft 5x = ln 3 dus x = (ln 3)/5 |
|||
| b. | fa(x)
= x eax geeft met de productregel en
de kettingregel: fa' (x) = 1 eax + x eax a Nul invullen geeft fa(0) = 11 + 01a = 1 |
||||
| 9. | a. | 100 = 200 - 180 e-0,29t
⇒ -100 = -180 e-0,29t ⇒ e-0,29t = 100/180 ⇒ -0,29t = ln(100/180) » -0,588 ⇒ t = -0,588/-0,29 ≈ 2,0268 uren en dat is 2,0268 60 = 121,6 minuten Dus ongeveer 2 minuten over 5 (17:02) wordt het opwarmen gestopt. |
|||
| b. | S'(t) = -180
e-0,29t -0,29 = 52,2 e-0,29t
S'(1) = 39,059 ΊC/uur en dat is 0,65 ΊC/minuut dus ongeveer 0,7 ΊC/minuut. |
||||
| c. | S - 200 = -180 e-0,29t
⇒ (S - 200)/-180
= e-0,29t 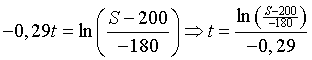
|
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||