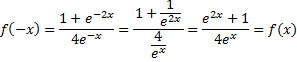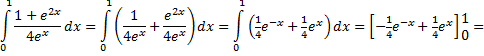|
|||||
| 1. | a. | P(t) = 0,8P0
geeft 0,8P0 = P0 e-0,000029t
0,8 = e-0,000029t Y1 = 0,8 en Y2 = e^(-0,000029X) en dan intersect geeft t = 7695 |
|||
| b. | P(t) = 100
e-0,000029t geeft P'(t)
= 100 -.000029 e-0,000029t P'(20000) = 100 -0,000029 e-0,000029 20000 = -0,0016 Dat stelt voor: de snelheid waarmee het stralingsniveau per jaar afneemt op tijdstip t = 20000 |
||||
| 2. | a. | 0,3I0 = I0
e-0,9 0,12 l 0,3 = e-0,108 l Y1 = 0,3 en Y2 = e^(-0,108X) en dan intersect geeft l = 11,1 meter |
|||
| b. | Als de intensiteit
afneemt met 1% per meter, dan is I ' = -0,01 I I' = I0 e-0,108 l -0,108 = -0,01 I0 e-0,108 l = 0,0926 Y1 = e^(-0,108X) en Y2 = 0,0926 en dan intersect geeft l = 22 meter |
||||
| 3. |
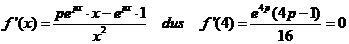 |
||||
| Daaruit volgt direct dat 4p - 1 = 0 dus p = 1/4 | |||||
| 4. | a. |
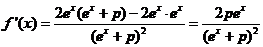 |
|||
| Dat kan alleen nul zijn als
2pex = 0 en dat is alleen zo als p = 0 Maar voor p = 0 is de functie gelijk aan f(x) = 2 en die heeft geen extremen. |
|||||
| b. |
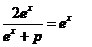 |
||||
| 2ex = ex
(ex + p) Noem nu ex = a dan staat hier 2a = a(a + p) 0 = a2 + a(p - 2) 0 = a(a + p - 2) a = 0 ∨ a = 2 - p ex = 0 ∨ ex = 2 - p De eerste heeft geen oplossing. ex = 2 - p heeft geen oplossing als p ≥ 2 Er zijn dus geen snijpunten als p ≥ 2 |
|||||
| 5. | a. |
|
|||
| Dat geeft 1 -
1/x
= 0 x = 1 en dan is y = e. Het minimum is het punt (1, e) |
|||||
| b. |
Als de raaklijnen in x = p en x = -p loodrecht op elkaar staan, dan moet gelden: f '(p) f '(-p) = -1 |
||||
|
|
|||||
| 1/p2
= 2 p2 = 1/2 p = ±√1/2 = ±1/2√2 |
|||||
| 6. | Voor de lengte L
geldt: L = x2 e-0,5x
- (x + 2) e-0,5x want voor
x > 2 ligt de grafiek van f boven die van g L is maximaal als de afgeleide nul is: L ' = 2x e-0,5x + x2 -0,5 e-0,5x - 1 e-0,5x - (x + 2) -0,5 e-0,5x = 0 e-0,5x (2x - 0,5x2 - 1 + 0,5x + 1) = 0 -0,5x2 + 2,5x = 0 x(-0,5x + 2,5) = 0 x = 0 ∨ x = 5 x = 5 geeft dan L(5) = 25 e-2,5 - 7 e-2,5 = 18 e-2,5 = 1,48 |
||||
| 7. | a. | x
≥ 2: f ' = 4 e(-0,5
+ 0,25x) 0,25 (die 0,25 komt van de kettingregel)
en f '(2) = 1 x ≥ 2: f ' = 3/2 - 1/2x en f '(2) = 1/2 |
|||
| b. | Bereken eerst de top: f '= 0 geeft 3/2 - 1/2x = 0 en dus x = 3, en y = 1 + 3.2 3 - 1/4 32 = 31/4. De grafiek moet dus 3 naar links geschoven worden en 31/4 omlaag. Dan moet x worden vervangen door (x + 3) en bovendien moet er -31/4 achter de hele formule gezet worden. Dat geeft: y = -1 + 4e(-0,5 + 0,24(x + 3)) - 31/4 |
||||
| 8. | a. | Voer de functie f
en de lijnen y = -0,1 en y = 0,1 in in de GR. Gebruik INTERSECT om de snijpunten te vinden. Dat geeft x = 0,11 en x = 3,58 en x = -0,09 Lees vervolgens af waar de grafiek van f tussen beide lijnen in ligt. Dat is zo voor -0,09 < x < 0,11 of x > 3,58 |
|||
| b. | Met de productregel
en de kettingregel: f '(x) = 1 e-x + x e-x -1 = e-x (1 - x) Voor de top geldt f '(x) = 0 dus e-x (1 - x) = 0 en dat is zo als x = 1 f (1) = 1 e-1 = 1/e de top is dus het punt (1 , 1/e) |
||||
| c. | A is het snijpunt van
de lijn y = 0,25x met
f(x) = x e-x dus moet
gelden 0,25x = x e-x
ofwel e-x = 0,25 e-x = 0,25 Y1 = e^(-X) en Y2 = 0,25 en dan intersect levert a = 1,386 |
||||
| d. | De
lengte ST is gelijk aan x e -x -
0,25x (het verschil van beide y -coφrdinaten) Voer deze vergelijking in in de GR en bereken met CALC - Maximum de maximale waarde van ST. Dat geeft x ≈ 0,562 en een maximum van STMAX ≈ 0,180 |
||||
| 9. | a. | 0,035 = 0,12 t
e-0,5t Deze moet met de GR: Y1 = 0,035 en Y2 = 0,12 X e ^(-0,5 * X) window bijv. Xmin = 0, Xmax = 10, Ymin = 0, Ymax = 0,1 intersect geeft twee snijpunten: t = 0,3469 en t = 6,0715 De tijd daartussen is 5,7246 5,7246 60 = 343 minuten |
|||
| b. | productregel: C ' = 0,12 1 e-0,5t + 0,12t e-0,5t -0,5 (de laatste -0,5 komt van de kettingregel) = 0,12 (1 e-0,5t - 0,5t e-0,5t) = 0,12 (1 - 0,5t) e-0,5t |
||||
| c. | De concentratie
neemt het sterkst af als C'(t) zo groot mogelijk negatief is. Plot de grafiek en bereken dat minimum met calc - minimum van je GR. Dat geeft t = 4 Het kan uiteraard ook algebraοsch: C'is minimaal als C'' = 0 C'' = 0,12 -0,5 e-0,5t + 0,12 (1 - 0,5t) e-0,5t -0,5 = e-0,5t (-0,06 - 0,06 + 0,03t) = e-0,5t (-0,12 + 0,03t) Dat is nul als -0,12 + 0,03t = 0 ⇒ t = 4 |
||||
| d. | Tussen t
= 18 en t = 24 geldt: C* = C(t) + C(t - 6) + C(t - 12) + C(t - 18) Voer in in de GR: Y1 = 0,12 X e ^(-0,5X) Y2 = Y1(X) + Y1(X - 6) + Y1(X - 12) + Y1(X - 18) (Y1 vind je bij VARS) Bepaal het maximum van Y2 tussen t = 18 en t = 24 Dat geeft een maximum van C = 0,1087 bij t = 19,68 De concentratie kom dus NIET boven de 0,11. |
||||
| 10. | a. | PQ
= PS geeft 2p = e-p² Y1 = 2X en Y2 = e^(-X^2) en dan intersect geeft p ≈ 0,41936 De oppervlakte is dan p2 ≈ 0,176 |
|||
| b. | De
oppervlakte is gelijk aan O = PQ PS = 2p e-p² Bij het maximum moet de afgeleide nul zijn. Met de productregel en de kettingregel: O' = 2 e-p² + 2p e-p² -2p = 2e-p² (1 - 2p2) O'= 0 ⇒ 1 - 2p2 = 0 ⇒ p2 = 1/2 ⇒ p = ±√(1/2) = ±1/2√2 Omdat p > 0 moet gelden p = 1/2√2. Het bewijs dat het inderdaad om een maximum gaat volgt uit het tekenbeeld van O', (0)+++++(1/2√2)-------- |
||||
| 11. | a. | Met de
kettingregel: U ' = 12 e(-t/20) -1/20
= -3/5 e(-t/20) Vul t = 0 in: U'(0) = -3/5 e0 = -3/5 (Volt/seconde) |
|||
| b. | Als
elke C gelijk is aan 0,01 en er zijn n condensatoren, dan geldt: (1/CS) = n (1/0,01) = 100n dus CS = 1/(100n) Deze vergelijking voor CS en t = 10 invullen in de formule voor U en gelijkstellen aan 10: |
||||
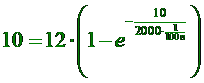 |
|||||
| Invullen in de GR: Y1 = 10 en Y2 = 12 * (1 - e ^
(-10/(2000/(100X)))) Intersect geeft n = 3,58... Er zijn dus 4 condensatoren nodig. |
|||||
| 12. | a. | f(x) = 10xe-x
f ' = 10e-x + 10xe-x · -1 = e-x · (10 - 10x) f '(0) = 10 dan is tanα = 10 ⇒ α = 84˚ |
|||
| b. | f ' =
e-x · (10 - 10x)
= 0 10 - 10x = 0 x = 1 f(1) = 10e-1 = 3,68 |
||||
| c. |
De helling van OA = y/x
= 10xe-x/x =
10e-x 10e-x = 2 e-x = 0,2 -x = ln(0,2) = -ln5 x = ln5 |
||||
| 13. |
fa(x) = a ex -
e2x fa' = aex - 2e2x fa ' = 0 ⇒ aex - 2e2x = 0 ⇒ ex(a - 2ex) = 0 ⇒ a = 2ex ⇒ ex = 0,5a ⇒ x = ln(0,5a) Dat betekent dat xU = ln(0,5a) xS = lna xS - xU = lna - ln(0,5a) = lna - ln(0,5) - lna = -ln(0,5) = ln2 Dat is inderdaad onafhankelijk van a |
||||
| 14. | a. | 1 + e2x
= 5/6 4 ex 6 + 6e2x = 20ex Noem ex = p dan staat er 6 + 6p2 = 20p 6p2 - 20p + 6 = 0 p = (20 ±√(256)/12 = 3 of 1/3 ex = 3 geeft x = ln3 ex = 1/3 geeft x = ln(1/3) = -ln3 |
|||
| b. | vervang x door -x: | ||||
|
|
|||||
| Bij die derde stap is
alles met e2x vermenigvuldigd. f(-x) = f(x) dus de grafiek is symmetrisch ten opzichte van de y-as. |
|||||
| c. |
|
||||
| = (-1/4e-1 + 1/4e) - (-1/4 + 1/4) = 1/4(e - 1/e) | |||||
| 15. | f(x) =
e geeft epx = e dus
px = 1 dus x = 1/p f '(x) = pepx dus f '(1/p) = pe De raaklijn is y = pex + b en gaat door (1/p, e): e = pe 1/p + b ⇒ b = 0 Dus de raaklijn gaat door de oorsprong. |
||||
| 16. | a. | f '(x)
= 2e2x en g'(x)
= 4e4x 2e2x = 4e4x noem nu e2x = p dan staat er 2p = 4p2 2p - 4p2 = 0 2p(1 - 2p) = 0 p = 0 ∨ p = 1/2. e2x = 0 geeft geen oplossing e2x = 1/2 ⇒ 2x = ln(1/2) ⇒ x = 1/2ln(1/2) |
|||
| b. | y = p p = e2x ⇒ 2x = lnp ⇒ x = 1/2lnp p = e4x ⇒ 2x = lnp ⇒ x = 1/4lnp De afstand daartussen is 1/2lnp - 1/4lnp = 1/4lnp = 1 lnp = 4 p = e4 en dat is de gevraagde y-waarde. |
||||
| 17. | P = (p,
ep) f'(x) = ex dus f '(p) = ep De raaklijn is de lijn y = ep x + b en gaat door (p, ep) Dat geeft ep = ep p + b dus b = (1 - p)ep en de raaklijn is de lijn y = ep x + (1 - p)ep A = (0, (1 - p)ep) dus OA = (1 - p)ep Voor B geldt: ep x + (1 - p)ep = 0 dus x = -(1 - p) dus OB = (1 - p) De oppervlakte is dan 0,5 (1 - p) (1 - p)ep = 0,5(1 - p)2 ep Dat is maximaal als de afgeleide nul is: (1 - p)ep + 0,5(1 - p2)ep = 0 ep(1 - p + 0,5 - 0,5p2) = 0 1,5 - p - 0,5p2 = 0 p2 - 2p - 3 = 0 (p + 1)(p - 3) = 0 p = -1 ∨ p = 3 p = -1 geeft maximale oppervlakte 2/e |
||||
| 18. | f ' = 1 eax
+ x a eax voor de top geldt f ' = 0 fa'(x) = eax+ axeax = 0 eax (1 + ax) = 0 eax = 0 ∨ 1 + ax = 0 ax = -1 (want eax kan niet nul zijn) x = -1/a y = xeax = x e-1 = 1/e x (want ax = a -1/a = -1) |
||||
| 19. | raaklijn in punt P: f '(p) = 1/p² e-1/p dus dat is de r.c. van de raaklijn. punt (p, e-1/p) invullen geeft e-1/p = 1/p² e-1/p p + b dat geeft b = e-1/p (1 - 1/p) raaklijn gelijkstellen aan nul: 1/p² e-1/p x + e-1/p (1 - 1/p) = 0 1/p² x = -1 + 1/p x = -p2 + p Dat is maximaal als de afgeleide ervan nul is: -2p + 1 = 0 Dus p = 1/2 Dan is x = 1/4 |
||||
| 20. | P
= (p, pep) en Q = (2p,
2pe2p) rc PQ is gelijk aan (2pe2p - pep)/(2p - p) = 6 2pe2p - pep = 6p Alles delen door p: 2e2p - ep = 6 Noem ep = a, dan is e2p = a2 Dat geeft 2a2 - a = 6 2a2 - a - 6 = 0 a = (1 ±√49)/4 a = 2 ∨ a = -1,5 ep = 2 ∨ ep = -1,5 (maar dat laatste kan niet) p = ln(2) |
||||
| 21. | Vierkant V heeft zijden p dus oppervlakte p2 Vierkant W heeft zijden ep dus oppervlakte e2p De verhouding is p²/e2p Dat is maximaal als de afgeleide ervan nul is. Met de quotiλntregel: |
||||
|
|
|||||
| Dat is
nul als de teller nul is: 2pe2p - 2p2
e2p = 0 2e2p(p - p2 ) = 0 p - p2 = 0 p(1 - p) = 0 p = 0 ∨ p = 1 p = 1 geeft R = 1/e² |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||