|
|||||
| 1. | Als f(x)
= eax dan is (met de kettingregel) f
'(x) = a • eax = a • f(x) Dus f '(x) = 3 • f(x) geldt voor f(x) = e3x f '(x) = -2 • f(x) geldt voor f(x) = e-2x |
||||
| 2. | a. | Als de palen 4 meter
uit elkaar staan, en het laagste punt ligt bij x = 0, dan bevinden de palen zich bij x = 2 en x = -2 a = 0,8 geeft y = 0,4 • (e1,25x + e-1,25x) De afgeleide is dan y' = 0,4 • (e1,25x • 1,25 + e-1,25x • -1,25) x = 2 geeft y' (2) = 0,4 • (e2,5 • 1,25 + e-2,5• -1,25) = 6,05 dat is de helling van de ketting, en die maakt met een horizontale lijn een hoek waarvoor tanα = 6,05, dus α = 81º dus de hoek met een verticale lijn (de paal) is 90 - 81 = 9º Vanwege de symmetrie is de hoek in het ophangpunt x = -2 dan -9º |
|||
| b. | x = 0 moet y = 2
geven. x = 0: 0,5 • a • (1 + 1) = 2 geeft a = 2 |
||||
| 3. | a. | A = (0, e-0)
= (0, 1) en B = (1, e-1) = (1,
1/e) AB heeft helling (1/e - 1) en dus vergelijking AB: y = (1/e - 1)x + 1 |
|||
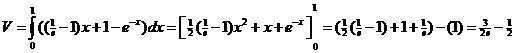 |
|||||
| b. | de helling van AB is
1/e - 1 dus moet de afgeleide van f ook gelijk zijn aan 1/e
- 1 f ' = -e-x = 1/e - 1 Y1 = -e^(-X) en Y2 = 1/e - 1 en dan intersect levert x = 0,46 |
||||
| 4. | De grafieken raken
elkaar als geldt f = g en f ' = g'
De eenvoudigste is de tweede, dus daar beginnen we mee: f ' = g' (met de productregel): (x2 - 2x + 1) • ex + (2x - 2) • ex = 3 • ex x2 - 2x + 1 + 2x - 2 = 3 x2 = 4 x = 2 ∨ x = -2 Dan f = g; (x2 - 2x + 1) • ex = 3 • ex + p x = 2 geeft e2 = 3e2 + p dus p = -2e2 x = -2 geeft 9e-2 = 3e-2 + p dus p = 6e-2 |
||||
| 5. | f '(x)
= e0,5 - x²
• -2x f '(1) = e-0,5 • -2 = -2/√e dus de raaklijn is de lijn y = -2/√e • x + b f(1) = e-0,5 = 1/√e dus moet gelden 1/√e = -2/√e • 1 + b ⇒ b = 3/√e De raaklijn is de lijn y = -2/√e • x + 3/√e y = 0 geeft dan 0 = -2/√e • x + 3/√e 2/√e • x = 3/√e x = 1,5 Het snijpunt met de x-as is (1.5, 0) |
||||
| 6. | Je vindt de extreme
waarde als de afgeleide nul is: f '(x) = (4x + p) • ex² • 2x + 4 • ex² = 0 ex² •(8x2 + 2px + 4) = 0 8x2 + 2px + 4 = 0 Dat heeft maar geen oplossing als de discriminant kleiner dan nul is: (2p)2 - 4 • 8 • 4 < 0 4p2 < 128 p2 < 32 -√32 < p < √32 ook bij p = ±√32 is er geen extreme waarde: dan vallen minimum en maximum samen en is er een buigpunt. |
||||
| 7. | a. | Bij het maximum is de afgeleide
nul: R' = 100 • e(-0,1t³ + 0,5t²) • (-0,3t2 + t) = 0 -0,3t2 + t = 0 t(-0,3t + 1) = 0 t = 0 ∨ t = 31/3 Het maximum vind je bij t = 31/3 en R(31/3) = 637 ratten |
|||
| b. | R'(4) = 100 • e(-0,1• 64 + 0,5• 16) • (-0,3•16 + 4) = -396 ratten per dag | ||||
| c. | plot: Y1 = 100*e^(-0,1*X^3+0,5*X^2) Y2 = nDeriv(Y1, X, X) calc - maximum - Y2 geeft dan t = 2,41 |
||||
| 8. | a. | 30 = 65 • e-0,012k
Y1 = 30 en Y2 = 65 * e^(-0,012X) en dan intersect geeft maximaal 64 andere kinderen |
|||
| b. | hoeveelheid snoep = aantal
kinderen * aantal snoepjes per kind H = k • S = k • 65 • e-0,012k H is maximaal als H' nul is: 1 • 65 • e-0,015k + k • 65 • e-0,012k• -0,012 = 0 e-0,012k • (65 - 0,78k) = 0 65 - 0,78k = 0 k = 83, 33 k = 83 geeft H = 1992,7 k = 84 geeft H = 1992,6 Dus H = 1992,7 is de maximale hoeveelheid snoep (bij 83 kinderen) |
||||
| 9. | De lengte van het
lijnstuk is L = f(p) - g(p) = x • e0,5x
-(e0,5x - 2) Dat is minimaal als de afgeleide ervan nul is: L' = 1 • e0,5x + x • 0,5 • e0,5x - 0,5 • e0,5x = 0 e0,5x • (1 + 0,5x - 0,5) = 0 1 + 0,5x - 0,5 = 0 x = -1 L(-1) = -1 • e-0,5 - (e-0,5 - 2) = 2 - 2e-0,5 = 2 - 2/√e |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||