© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. E(t) = 100 – (100 – B)·0,7t 
Als t oneindig groot wordt, dan wordt 0,7t  gelijk aan nul.
Maar dan wordt  (100 - B) • 0,7t   ook nul, dus gaat E naar 100.
De horizontale asymptoot is de lijn E = 100
Dat betekent in praktijk dat je nooit meer dan 100% ergens van kunt leren. Hoe langer je leert des te dichter nader je de 100%.
       
  b. 58 minuten is  58/15 = 3,867  kwartier
80 =  100 – (100 – B)·0,7,867  
-20 = -(100 - B) • 0,2518
100 - B = 79,43
B = 20,6%  		 
       
  c. strategie I
eerst een half uur leren, dan kent hij  E = 100 - 100 • 0,72 = 51%
dan nog 2,5 uur vergeten:   E = 51 • 0,9810 = 41,67%

strategie II.
eerst een kwartier leren:  E = 100 - 100 • 0,71 = 30%
dan een uur vergeten:  E = 30 • 0,984 = 27,67%
weer een kwartier leren:  E = 100 - (100 - 27,67) • 0,71 = 49,37%
dan nog 1,5 uur vergeten:  E = 49,37 • 0,986 = 43,73%

Met de tweede strategie weet hij na 3 uur het meest.
       
2. a.
tijd (min) 0 10 20 30 40
T(ΊC) 20 17 14,6 12,68 11,144
V(ΊC) 15 12 9,6 7,68 6,144
 
    de onderste rij gaat steeds keer 0,8  
       
  b. V gaat steeds keer 0,8 dus is exponentieel met g = 0,8
De beginwaarde is V = 15, dus de formule is  V = 15 • 0,8t
       
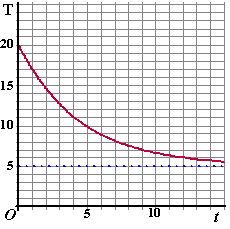
  c. T = V + 5  dus  T(t) = 5 + 15 • 0,8t
De grafiek zie je hiernaast
Horizontale asymptoot is de lijn  T = 5

     
  d. 6 = 5 + 15 • 0,8t
Y1 = 6  en  Y2 = 15 * 0,8^X en dan intersect levert  t = 12,14 uur
       
3. a. H(t) =  c - a • bt 
Als t oneindig groot wordt, dan wordt  a • bt  nul, dus dan gaat de grafiek naar c.
Uit de grafiek lees je af dat c = 800

H(0) = 800 - a • b0 = 800 - a  = 100  dus  a = 700

bijv (2, 400) invullen:   400 = 800 - 700 • b2
700 • b2 = 400
b2 = 400/700 = 0,5714
b = √0,5714 = 0,76
       
  b. Een afname van 0,03% per dag betekent dat er 99,97% overblijft, dus een groeifactor van 0,9997 per dag
Per jaar is dat  0,9997365 = 0,8963
0,8963 = ex  geeft  x = ln0,8963 = -0,11
Beginwaarde B = 11000 geeft dan   N = 11000 • (e-0,11)t = 11000 • e-0,11t 
       
  c. Totale gewicht = F(t) • N(t) = (0,600 - 0,535 • e-0,37t) •  11000 • e-0,11t 
= 0,6 • 11000 • e-0,11t  - 0,535 • e-0,37t •  11000 • e-0,11t
= 6600 • e-0,11t  - (0,535 • 11000)• e-0,37t • e-0,11t  
= 6600 • e-0,11t  - 5885 • e-(0,37 + 0,11)t
= 6600 • e-0,11t  - 5885 • e-0,48t 
       
  d. Y1 = 6600 • e^(-0,11*X)  - 5885 • e^(-0,48*X)  en dan calc - maximum   geeft  t = 3,672 jaren
Dat is 44 maanden na uitzetten.
       
4. a. Hoeveelheid vocht:  beginwaarde is 80% en elk uur wordt er 10% onttrokken, dus blijft er 90% over.
De hoeveelheid vocht is dus  80 • 0,90t
De totale hoeveelheid materiaal  is 20% NIET-vocht plus de hoeveelheid vocht, dus dat is  20 + 80 • 0,90t
Het percentage vocht is dan  vocht/totaal • 100  en invullen geeft precies de gevraagde formule.
       
  b. Noem 0,90t  even zolang X.
Dan staat er  30 = 100 • 80X/(20 + 80X) 
30(20 + 80X) = 100 • 80X
600 + 2400X = 8000X
600 = 5600X
X = 600/5600 = 0,1071
0,90t = 0,1071
t = log(0,1071)/log(0,90) = 21,2 uur
       
5. a. T wordt van positief later negatief en dat kan niet met een exponentiλle functie.
       
  b.
t in uren 0 1 2 3 4 5 6 7
T in ΊC 20,0 9,5 2,2 -3,0 -6,6 -9,1 -10,9 -12,1
Verschil V 35,0 24,5 17,2 12,0 8,4 5,9 4,1 2,9
       
    De factoren voor V zijn;
24,5/35 = 0,70  en  17,2/24,5 = 0,70  en  12,0/17,2 = 0,70  en  8,4/12,0 = 0,70 en  5,9/8,4 = 0,70 en 4,1/5,9 = 0,69 en 2,9/4,1 = 0,71
Dat is steeds ongeveer 0,7 dus de groeifactor voor V is 0,7.
De beginwaarde is 35 dus een formule voor V is  V = 35 • 0,7t
T = V - 15
Dus  T = 35 • 0,7t - 15 
       
6. a. begin van de tweede dag:  485 g ureum
eind van de tweede dag  485 + 500 = 985 g ureum
's nachts verversen:  0,97 • 985 = 955,45 g ureum en dat is aan het begin van de derde dag
       
  b. begin vierde dag:  0,97(955,45 + 500) = 1411,79
begin vijfde dag:  0,97(1411,79 + 500) = 1854,43
in de loop van de vijfde dag komt er 500 bij, dus zal de norm (2000) worden overschreden.
       
  c. Er wordt 200 m3 van de 1000 m3 ververst, dus er blijft  800 m3 over en dat is 80%.
De groeifactor is daarom 0,80
Als er het begin van een dag U gram is, dan is er het eind van die dag  U + 500 gram.
Daar blijft bij verversen 80% van over:  0,8(U + 500) = 0,8U + 400
       
  d. 2500 • 0,8n  is altijd positief, dus is  2000 - 2500 • 0,8n  altijd kleiner dan 2000
       
  e. De norm wordt in de loop van een dag overschreden als aan het begin van een dag er meer dan 1500 gram aanwezig is.
Y1 =  2000 - 2500 • 0,8^X
Kijk in TABLE wanneer dat voor het eerst groter dan 1500 is
Dat geeft  n = 8 
       
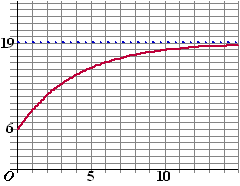
7. a. Zie hiernaast.
De asymptoot is de lijn T =19

     
  b. De omgevingstemperatuur si de temperatuur die de fles uiteindelijk zal krijgen en die is 19 ΊC
De koelkasttemperatuur is de temperatuur die de fles in het begin heeft, en die is 6ΊC
     
  c. (0, 6)  en  (0.01,  6.0322)
Δy/Δx = (6,0322 - 6)/(0,01 - 0) = 3,22 ΊC/min.
       
  d. 19 - 13 • 0,78t  = 6 + 13 • 0,78t 
13 = 26 • 0,78t
0,78t = 0,5
t = log(0,5)/log(0,78) = 2,8 min.
       
  e. 14 = 16 - 11 • g15
11 • g15 = 2
g15 = 0,1818
g = 0,18181/15 = 0,89
       
8. a. y = at + b kan niet omdat elk jaar steeds meer verdwijnt. Met dit lineaire model zou elk jaar evenveel verdwijnen.
y = agt  zou afname geven als g < 1, maar dan zou die afname steeds minder snel gaan in plaats van steeds sneller.
       
  b. afname in 1980:  y(0) = 3311 - 274 • 1 = 3037  en  y(1) = 3311 - 274 • 1,0414 = 3025,65
dat geeft afname  3037 - 3025,65 = 11,35

afname in 1990:  y(10) = 3311 - 274 • 1,041410 = 2899,92  en   y(11) = 3311 - 274 • 1,041411 = 2882,90
dat geeft afname 2899,92 - 2882,90 = 17,02

17,02 is inderdaad ongeveer 1,5 keer  11,35
17,02 klopt met de hoeveelheid die in 1990 verdween
op 1 januari 1990 was inderdaad nog ongeveer 2900 miljoen ha over.  
       
  c. 1000 = 3311 - 274 • 1,0414t
274 • 1,0414t = 2311
1,0414t = 8,434
t = log(8,434)/log(1,0414) = 52,56 jaar
Dat zal zijn in het jaar 2032
       
  d. als de bosoppervlakte in de periode 1985-200 weer met 5% toeneemt zal er in 2000:   2100 • 1,05 = 2205 miljoen ha zijn.

van het tropisch oerwoud zal er  3311 - 274 • 1,041420 = 2694 miljoen ha zijn.

de bosoppervlakte zal nog niet groter zijn.

       
9. a. Het aantal uilen is met een factor 178/20 = 8,9 toegenomen in een periode van 12 jaar.
De groeifactor per jaar is dan  8,91/12 = 1,19981...  en dat is ongeveer 20% per jaar.
       
  b. t = 0 en 178 uilen geeft  178 = a - b • 0,60 dus  178 = a - b
t = 2 en 205 uilen geeft  205 = a - b • 0,62 dus  205 = a - 0,36b
Uit beide vergelijkingen samen moeten a en b opgelost worden.
De eerste geeft  a = b + 178 en dat kun je invullen in de tweede:  205 = b + 178 - 0,36b
Dus  205 - 178 = b - 0,36b  ⇒  27 = 0,64b  ⇒   b = 27/0,64 = 42,1875
Invullen in de eerste vergelijking geeft a = b + 178 = 42,1875 + 178 = 220,1875
Conclusie:  a = 220,19  en  b = 42,19 
       

© h.hofstede (h.hofstede@hogeland.nl)