|
|||||||||
| 1 | a. | 2,4 =
2,7 – 0,058G -0,3 = -0,058G G = 5,17% |
|||||||
| b. | G = 6 geeft T =
2,7 - 0,058 • 6 = 2,352 één graad lager geeft T = 1,352 1,352 = 2,7 - 0,058G -1,348 = -0,058G G = 23,24% Dus er moet 23,24 - 6 = 17,24% bijgeplant worden. 6% is 38km2 dan is 17,24% gelijk aan 17,24 • 38/6 = 109 km2 |
||||||||
| c. |
T = 2,7 – 0,058G T - 2,7 = -0,058G T/-0,058 - 2,7/-0,058 = G -17,24T + 46,55 = G |
||||||||
| d. |
3,0 – 0,084G = 2,7 – 0,058G 0,3 = 0,026G G = 11,54% |
||||||||
| 2. | a. | We hebben de twee punten (12,
111.9) en (110, 101.0) a = Δy/Δx = (101.0 - 111.9)/(110 - 12) = -10.9/98 = -0,111 111.9 = -0,111 • 12 + b geeft dan b = 113,23 De formule is dan y = -0,111t + 113,23 |
|||||||
| b. | De punten rondom 1951 zijn
(36, 109.7) en (55, 105.7) Reken vanaf het eerste punt. |
||||||||
|
|||||||||
| ?? = -4 • 15/19
= -3,16 Dan is de waarde in 1951 gelijk aan 109,7 - 3,16 = 106,54 dus 1 : 46,54 |
|||||||||
| c. | 95 =
-0,125t + 113,4 -18,4 = -0,125t t = 147,2 Dat zal zijn in 2047 |
||||||||
| d. | het hellinggetal -0,212 is groter en dat geeft aan hoe snel de verandering is. | ||||||||
|
-0,125t + 113,4
= -0,212t + 163,9 0,087t = 50,5 t = 580,5 Dat zal zijn in 2480 |
|||||||||
| 3. | a. | T = 0,2 × 40 + 10 = 18ºC | |||||||
| b. | 15 = 0,2
× S + 10 5 = 0,2T T = 25 ºC |
||||||||
| c. | Trek 25 af: S - 25 deel door 5: (S - 25)/5 = S/5 - 25/5 = 0,2S - 5 tel er 10 bij op: 0,2S - 5 + 10 Dus T = 0,2S + 5 Dat is anders dan de regel van Dekkers, namelijk steeds 5 C lager. |
||||||||
| 4. | a. | Het getal waar T mee wordt vermenigvuldigd (-1,2) is negatief. Dus als T groter wordt, dan wordt H kleiner. | |||||||
| b. | 7
= 12 – 1,2T -5 = -1,2T T = 25/6 |
||||||||
| 5. | a. | Het bedrag per kilometer is het
hellinggetal. Het bedrag voor de wagen is het begingetal. KB = 400 + 2,5a KM = 550 + 1,6a |
|||||||
| b. | 400 + 2,5a = 550 + 1,6a 0,9a = 150 a = 1662/3 km. Voor afstanden boven de 1662/3 km. is Mast het goedkoopst. |
||||||||
| c. | Het eerste deel, want de grafiek daarvan gaat door de oorsprong, en dat moet voor een evenredig verband. | ||||||||
| d. | De grafiek gaat door (100, 700) en (200,
1900) a = Δy/Δx = (1900 - 700)/(200 - 100) = 12 Eerste punt invullen: 700 = 12 • 100 + b geeft dan b = -500 De vergelijking is dan y = 12x - 500 |
||||||||
| 6. | a. | P =
5,5 geeft 5,5 + (18 - T)/30 • 94,5 = 5,5 twee manieren: 1. met de GR: voer in Y1 = 5,5 + (18 - X)/30*94,5 en Y2 = 5,5 intersect levert T = 18ºC 2. algebraïsch:
5,5 + (18 - T)/30 • 94,5 = 5,5 |
|||||||
| b. | Vul in
T = -12 Dat geeft P = 5,5 + 30/30 • 94,5 = 5,5 + 94,5 = 100% Dat is de maximale capaciteit. (en T > -12 geeft nog geen 100%) |
||||||||
| c. | 5,5 + (18 - T)/30 •
94,5 = 5,5 + (18 - T) • 94,5/30 = 5,5 + (18 - T) • 3,15 = 5,5 + 3,15 • 18 - 3,15 • T = 5,5 + 56,7 - 3,15 • T = 62,2 - 3,15 • T Dus a = -3,15 en b = 62,2 |
||||||||
| 7. | a. | Voor 2007 is het
vastrecht 52,80 en het tarief per m3 1,10. De formule daarbij is B = 1,10x + 52,80 Voor 2006 is het vastrecht 47,52 en het tarief per m3 1,24 De formule daarbij is B = 1,24x + 47,52 Gelijkstellen: 1,10x + 52,80 = 1,24x + 47,52 ⇒ 0,14x = 5,28 ⇒ x = 37,71 Dus vanaf 37,71 m3 ben je in 2007 goedkoper uit dan in 2006. |
|||||||
| b. | De grafiek gaat
door (ongeveer) (0, 1.0) en (6, 2.4) De helling is dan Δy/Δx = (2,4 - 1)/(6 - 0) = 0,233 ≈ 0,2 Het begingetal is 1,0 Dan wordt de formule V = 0,2 • t + 1,0 Dus a = 0,2 en b = 1,0 |
||||||||
| c. | In 2004 is het
verbruik (aflezen) 3 liter per persoon per dag. Dan is het totale verbruik van heel Nederland 3 • 16 miljoen = 48 miljoen liter Maar er waren maar 0,58 • 16 miljoen = 9,28 miljoen Nederlanders die "echt"een vaatwasmachine hadden. Dan is het verbruik per persoon 48 miljoen/9,28 miljoen = 5,2 liter per persoon per dag. |
||||||||
| 8. | Lees bijv. af C = 60, F =
140 en C = 80, F = 175 C = ..... Δy/Δx = (80 - 60)/(175 - 140) = 0,57 60 = 0,57 • 140 + b geeft dan b = -19,6 Dus C = 0,57F - 19,6 F =.... Δy/Δx = (175 - 140)/(80 - 60) = 1,75 140 = 1,75 • 60 + b geeft dan b = 35 Dus F = 1,75C + 35 |
||||||||
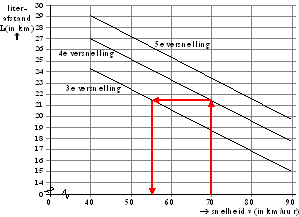
| 9. | a. | zie de figuur
hiernaast. ga bij 70 km/uur verticaal omhoog naar de lijn van de 4e versnelling. Dat geeft de literafstand (ongeveer 21,5). Ga daarna horizontaal opzij naar de lijn van de 3e versnelling (blijf dus bij dezelfde literafstand) Ga dan verticaal omlaag om te kijken welke snelheid daarbij hoort. Het is ongeveer 55 km/uur |
 |
||||||
| b. | Als de
lijnen evenwijdig zijn, dan zal de formule er uitzien als L =
-0,1838 • v + b (immers dezelfde lijnen hebben hetzelfde hellinggetal) Vul een punt van de grafiek in, bijvoorbeeld (90, 15) 15 = -0,1838 • 90 + b ⇒ 15 = -16,542 + b ⇒ b = 31,542 De formule is L = -0,1838 • v + 31,542 |
||||||||
| c. | L =
-0,1838 • v + 36,38 L - 36,38 = -0,1838 • v L/-0,1838 - 36,38/-0,1838 = v L • 1/-0,1838 + 197,9 = v -5,4L + 197,9 = v |
||||||||
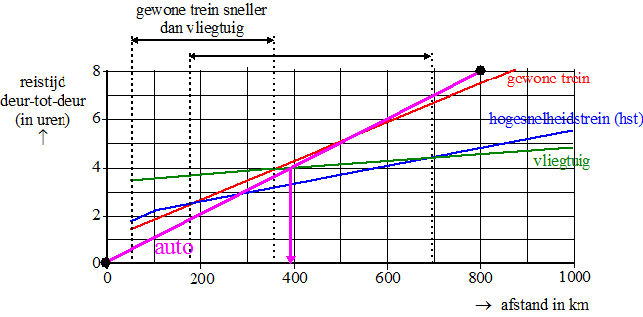
| 10. | a. | De grafiek van de
hst gaat door bijv. (300, 3) en (1000, 5.5) Dat betekent in 5,5 - 3 = 2,5 uur een afstand van 1000 - 300 = 700 km De snelheid is dan 700/2,5 = 280 km/uur |
|||||||
| b. |
|
||||||||
| De grafiek van de
auto is een rechte lijn tussen (0, 0) en (800, 8). Zie de paarse lijn hierboven. Die snijdt de grafiek van het vliegtuig ongeveer bij 400 km De auto is sneller voor afstanden van 0 - 400 km |
|||||||||
| c. | De reistijden zijn
gelijk als 0,00137a + 3,43 = 0,00793a + 1,10 2,33 = 0,00656a a = 2,33/0,00656 = 355 km In de grafiek zie je dat voor afstanden vanaf 355 km het vliegtuig een kleinere reistijd heeft. |
||||||||
| 11. | a. | fase 1: beginpunt
2500. Helling -1500/25 = -60 dus h(a)
= -60 • a + 1500 fase 2: helling -1000/15 = -662/3 0 = -662/3 • 50 + b geeft dan b = 13331/3 dus h(a) = -662/3 • a + 13331/3 |
|||||||
| b. | helling -2500/35 = -71,4 0 = -71,4 • 50 + b geeft b = 3571,4 dus h(a) = -71,4 • a + 3571,4 |
||||||||
| 12. | a. | 1900: (0, 163) dus
b = 163 1996: (96, 175) a = Δy/Δx = (175 - 163)/(96 - 0) = 0,125 |
|||||||
| b. | 168 = 163 + 0,125t 5 = 0,125t t = 40 dus dat was in 1940 |
||||||||
| c. | 163 + 0,125t = 161,5 +
0,138t 1,5 = 0,013t t = 115,4 In het jaar 2015 zal Duitsland Nederland inhalen. |
||||||||
| 13. | a. | (150 kg, 70 gram) en (520 kg, 180
gram) a = Δy/Δx = (180 - 70)/(520 - 150) = 0,297 70 = 0,297 • 150 + b geeft dan b = 25,45 H = 0,297 • L + 25,45 |
|||||||
| b. | L = 180 kg; model II: H = 0,28 • 180 + 26,5 = 76,9 grafiek H = 140 gram. Dat scheelt 63,1/76,9 = 82% |
||||||||
| c. | 0,32L + 24,2 = 0,28L + 26,5 0,04L = 2,3 L = 57,5 kg. |
||||||||
| 14. | a. | Dat is het aantal graden dat de gemiddelde temperatuur per jaar toeneemt. | |||||||
| b. | 12 = 0,016t + 8,48 3,52 = 0,016t t = 3,52/0,016 = 220 Dat zal zijn in het jaar 2120 |
||||||||
| c. | 0,018t + 7,90 =
0,016t + 8,48 0,002t = 0,58 t = 0,58/0,002 = 290 Dat zal zijn in het jaar 2190 |
||||||||
| 15. | a. | K = 0,053 • 200 • (L + 2) K = 10,6(L + 2) K = 10,6L + 21,2 Dat is een rechte lijn met helling 10,6 en begingetal 21,2. 10,6 stelt voor: per jaar moet een kind 10,6 mg méér van het geneesmiddel krijgen. |
|||||||
| b. | V = K als 0,053(L +
2) = 1 0,053L + 0,106 = 1 0,053L = 0,894 L = 0,894/0,053 = 16,9 jaar. |
||||||||
| c. | 0,5V = 0,053 • V • (L + 2) 0,5 = 0,053(L + 2) 0,5 = 0,053L + 0,106 0,053L = 0,394 L = 0,394/0,053 = 7,4 |
||||||||
| 16. | a | in
2009 is de prijs 18, en in 2021 is de prijs 8 Dat geeft de punten (0, 18) en (12, 8) a = (8 - 18)/(12 - 0) = -10/12 = -5/6 b = 18 want de lijn gaat door (0, 18) De formule is kz = -5/6 • t + 18 Als ze evenveel kosten moet gelden -5/6t + 18 = -0,31t + 10,0 -0,5233...t = -8 t = 15,28.... Dat is in het jaar 2024. |
|||||||
| b. | km
= 2 • kl 0,28t + 4,3 = 2 • (-0,31t + 10,0) 0,28t + 4,3 = -0,62t + 20,0 0,90t = 15,7 t = 15,7/0,90 = 17,44.... Dat is dus in het jaar 2026. |
||||||||
| 17. | a. | (C,
F) is (0, 32) en (37, 96) rc is (96 - 32)/(37 - 0) = 1,729... F = 1,729C + 32 0 = 1,729C + 32 C = -18,5 |
|||||||
| b. | C
= F C = 5/9 • (C - 32) C = 5/9C - 17,77... 4/9C = -17,77... C = -40 °C |
||||||||
| c. | K
= C + 273,15 K = 5/9 • (F - 32) + 273,15 K = 5/9F - 5/9 • 32 + 273,15 K = 0,56F + 255,37 a = 0,56 en b = 255,37 |
||||||||
| d. | De
lijnen van Fahrenheit en Rankine zijn evenwijdig dus hebben ze dezelfde
richtingscoëfficiënt. Dat betekent dat p = 5/9 = 0,56 0 °RA = 0 °K = -273,15 °C Dus q = -273,15 |
||||||||
| 18. | a. | (C,
F) is (0, 32) en (37, 96) rc is (96 - 32)/(37 - 0) = 1,729... F = 1,729C + 32 0 = 1,729C + 32 C = -18,5 |
|||||||
| b. | C
= F C = 5/9 • (C - 32) C = 5/9C - 17,77... 4/9C = -17,77... C = -40 °C |
||||||||
| c. | K
= C + 273,15 K = 5/9 • (F - 32) + 273,15 K = 5/9F - 5/9 • 32 + 273,15 K = 0,56F + 255,37 a = 0,56 en b = 255,37K = C + 273,15 K = 5/9 • (F - 32) + 273,15 K = 5/9F - 5/9 • 32 + 273,15 K = 0,56F + 255,37 a = 0,56 en b = 255,37 |
||||||||
| d. | De
lijnen van Fahrenheit en Rankine zijn evenwijdig dus hebben ze dezelfde
richtingscoëfficiënt. Dat betekent dat p = 5/9 = 0,56 0 °RA = 0 °K = -273,15 °C Dus q = -273,15 |
||||||||
| 19. | a. | 1 juli
1020: t = 0 geeft P = 25,93 1 juli 2040: t = 21,5 geeft P = -0,61 · 21,5 + 25,93 = 12,815% Dat is inderdaad (iets meer dan)een halvering. |
|||||||
| b. | 1995
geeft t = 5 en P = 29 2004 geeft t = 14 en P = 26 a = (26 - 29)/(14 - 5) = -0,333.... 29 = -0,333.. · 5 + b geeft dan b = 30,666... afgerond dus a = -0,273 en b = 30,667 |
||||||||
| c. | In
2018 is de waarde van formule 2 gelijk aan Pv
= -0,33 · 28 + 30,67 =
21,43 De formule voor de vrouwen met t = 0 in 2018 wordt dan Pv = -0,33 · t + 21,43 Stel die gelijk aan de mannenformule: -0,33 · t + 21,43 = -0,61t + 25,93 0,28t = 4,50 t = 4,50/0,28 = 16,07... Dat is in 2034 |
||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||