© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. P= (2, 4) en Q = (1,1) dus PQ heeft helling 3
PQ heeft vergelijking  y = 3x + b en moet door (1,1) gaan, dus  1 = 3 • 1 + b   ⇒  b = -2
PQ is dus de lijn  y = 3x - 2
y = 2 geeft dan  2 = 3x - 2  ⇒ 3x = 4 ⇒  x = 4/3

y = 2 geeft met y = x2 dat x2 = 2  ⇒  x = √2
Afstand ST is dan  √2 - 4/3  = 0,08  
       
  b. Q = (a, a2 )  en  P = (2, 4)
r.c. = Δy/Δx = (4 - a²)/(2 - a)  = (2 - a)(2 + a)/(2 - a) = 2 + a
       
  c. PQ is de lijn y = (2 + a)x + b en die moet door P(2, 4) gaan.
4 = (2 + a) • 2 + b
4 = 4 + 2a + b
b = -2a
PQ is dus y = (2 + a) • x - 2a
S ligt op y = 2:   2 = (2 + a) • xS - 2a
2 + 2a = (2 + a) • xS 
xS = (2 + 2a)/(2 + a)

2 - 2/(2 + a) = 2(2 + a)/(2 + a)  - 2/(2 + a)  =  (4 + 2a)/(2 + a) - 2/(2 + a) = (2 + 2a)/(2 + a)

Dat is inderdaad gelijk aan xS.
       
  d. T = (√2, 2)  en  xS = 2 - 2/(2 + a)
ST = √2 - (2 - 2/(2 + a))
ST = 0,01   
√2 - 2 + 2/(2 + a) = 0,01
2/(2 + a) = 0,01 + 2 - √2 ≈ 0,59579
2 + a =  2/0,59579 = 3,3569 ≈ 3,36
a = 1,36
Dus voor  1,36 < a < 1,41  (dat is √2),  is de waarde van ST kleiner dan 0,01.
       
2. Dan moet gelden  3√x = 2 • x2
9x = 4x4
4x4 - 9x = 0
x(4x3 - 9) = 0
x = 0  ∨  4x3 = 9
x = 0  ∨  x3 = 9/4 = 2,25
x = 0  ∨  x = (2,25)1/3 
       
3. Noem die lengte L dan geldt:   L(x) =  ex - e2x
Dat is maximaal als de afgeleide ervan nul is.
L' = ex - 2e2x  = 0
ex(1 - 2ex) = 0
ex = 0   ∨   1 - 2ex = 0
ex = 0  kan niet dus blijft over:  2ex = 1 ⇒  ex = 1/2 ⇒ x = ln(1/2)
Dan is  L = eln0,5 - e2ln0,5 = 0,5 - 0,52  = 1/4.
       
4. a. f - g = 1/6   (want voor a > 1 ligt f boven g)
1/x - 1/x2 = 1/6
x - 1 = 1/6 • x2
6x - 6 = x2
x2 - 6x + 6 = 0
ABC-formule:  x = (6 ± √(36 - 24))/2  = (6 ± √12)/2 = (6 ± 2√3)/2 = 3 ±√3
       
  b. 1/√b - 1/b moet maximaal zijn, dus moet de afgeleide ervan nul zijn.
1/√b - 1/b = b-0,5 - b-1
De afgeleide is dan   -0,5b-1,5 + b-2 = 0
Vermenigvuldig met b2 :   -0,5b0,5 + 1 = 0
0,5b0,5 = 1
b0,5 = 2
b = 4
Dan is de lengte  1/√4 - 1/4 = 1/2 - 1/4  = 1/4		  
       
5. B = (p, 2p3)  dus met Pythagoras geeft dat, dat BO = √(p2 + (2p3)2)
AO = 3p
Dus moet gelden:  √(p2 + (2p3)2) = 3p
p2 + 4p6 = 9p2
4p6 - 8p2 = 0
4p2(p4 - 2) = 0
p = 0 ∨  p4 = 2
p = 0  ∨  p = ± 21/4
de gezochte oplossing is  p = 21/4
       
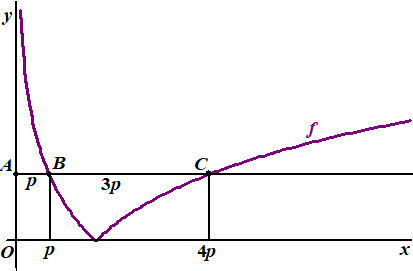
6.
  er geldt  f(p) = f(4p)  zie de figuur.
| lnp | = | ln(4p) |
Dat geeft:  lnp = ln4p of  lnp = -ln(4p)
De eerste heeft geen oplossing.

lnp = -ln(4p) = -ln4 - lnp
2lnp = -ln4
lnp = 1/2ln4 = ln41/2 = ln2
p = 2
Dan is q = | lnp |  = ln2
       
7. a. M is het midden van AS dus g ontstaat uit f door een vermenigvuldiging tov de y-as met factor 0,5
Dan is g(x) = √(2x)
xA = 1 = xN
yN = √(2 • 1) = √2
       
  b. A = (1,1)
OA = √(12 + 12) = √2
B = (b, √b)
AB = √((b - 1)2 + (√b - 1)2)

OA = AB  geeft √2 = √((b - 1)2 + (√b - 1)2)
Invoeren in de GR bij Y1 en Y2 en dan intersect geeft  b = 2,31
       

© h.hofstede (h.hofstede@hogeland.nl)