|
|||||
| 1. | a. |
|
|||
| b. |
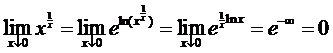 |
||||
| c. |
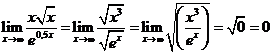 |
||||
| d. |
|
||||
| e. |
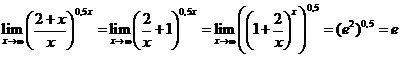 |
||||
| f. |
|
||||
| g. |
|
||||
| h. |
|
||||
| i. |
|
||||
| j. |
|
||||
| k. |
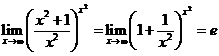 |
||||
| l. |
|
||||
| 2. | voor x van de
bovenkant naar nul gaat 1/x naar +∞
dan gaat e1/x ook naar oneindig, en de hele limiet dus ook. voor x van de onderkant naar nul
gaat 1/x naar -∞ |
||||
|
|
|||||
| de afgeleide functie is: | |||||
|
|
|||||
| als x van de
onderkant naar nul gaat, dan gaat 1/x
naar -∞ noem weer p = 1/x dan geeft dat voor de limiet: |
|||||
|
|
|||||
| de ep wint van beide machten van p dus de limiet is 0. | |||||
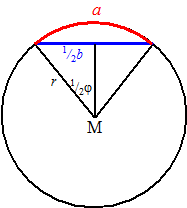
| 3. | 0,5b = r
• sin(0,5φ) dus b =
2r sin0,5φ a = rφ a/b = φ/2sin0,5φ = 0,5φ/sin0,5φ Dat laatste gaat naar 1 als φ naar nul gaat (standaardlimiet) Dus a/b gaat naar 1. |
 |
|||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||