© h.hofstede (h.hofstede@hogeland.nl)

       
1. a.
       
  b.  
       
  c.  
     
       
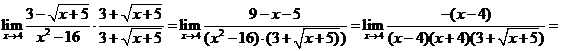  d.
       
  e. twee staartdelingen:  
   
     
     
       
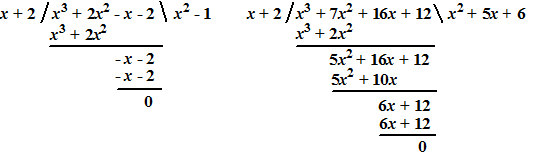  f.
    =-1/4·8 = -1/32  
       
  g. twee staartdelingen:  
   
   
       
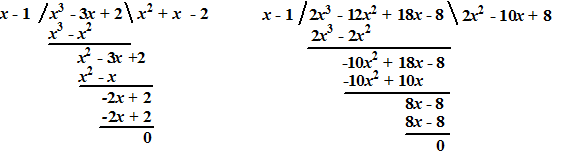  h. twee staartdeliungen:  
   
       
     
       
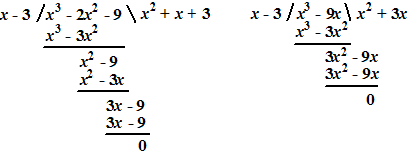2.
  Dan is  tan(2x)/tan(x) = 2/(1 - tan2x)
       
  a. Asymptoten bij  tan2x = 1  en dat is bij  x = 1/4π + k1/2π
Ophefbare discontinuïteit bij tanx = 0 en dat is bij x = 0 + kπ
Als tanx oneindig groot wordt, dan wordt 2/(1 - tan2x) gelijk aan 0
Dat betekent dat er ook ophefbare discontinuïteiten zijn bij x = 1/2p + kπ
       
  b. Je vindt de toppen als de afgeleide nul is:
-2 • (1 - tan2x)-2 • -2tanx • (tan2x + 1) = 0
dat kan alleen als  tanx = 0, dus bij  x = 0 + kπ
Maar daar bestaat de functie niet, dus is er een ophefbare discontinuïteit.
2/(1 - tan20) = 2  en  2/(1-tan2p) = 0  dus die ophefbare discontinuïteiten zijn de punten (0 + k2π, 2) en (π + k2π, 0)
De functie kan dus de waarden  [0, 2]  NIET aannemen.
       
3. a. -1 ≤ cos(1/x) ≤ 1
-x3  ≤  x3 • cos(1/x) ≤ x3
de rechter- en de linkerfunctie gaan beiden naar nul als x naar nul gaat, dus de middelste ook.
       
  b. -1 < sin(π/x) < 1
e-1  <  esin(π/x)  < e1
xe-1 <  x esin(π/x)  < xe1
de rechter- en de linkerfunctie gaan beiden naar nul als x naar nul gaat, dus de middelste ook.
       

© h.hofstede (h.hofstede@hogeland.nl)