|
© h.hofstede (h.hofstede@hogeland.nl) |
|||
 |
|||
| 1. | a. | sin(65) = x/14 x = 14 · sin(65) = 12,69 |
|
| b. | sin(54) = 15/x x = 15/sin(54) = 18,54 |
||
| c. | cos(x) = 4/7 x = cos-1(4/7) = 55,15° |
||
| d. | tan(x) = 6/9 x = tan-1(6/9) = 33,69° |
||
| e. | cos(48) = x
/15 x = 15 · cos(48) = 10,04 |
||
| f. | tan(50) = 10/x x = 10/tan(50) = 8,39 |
||
| g. | cos(x) = 4/20 x = cos-1(4/20) = 78,46° |
||
| h. | sin(44) = 9/x x = 9/sin(44) = 12,96 |
||
| i. | tan(80) = x/10 x = 10 · tan(80) = 56,71 |
||
| j. | cos(75) = 13/x x = 13/cos(75) = 50,22 |
||
| k. | tan(x) = 9/8 x = tan-1(9/8) = 48,37° |
||
| l. | sin(x) = 14/17 x = sin-1(14/17) = 55,44° |
||
| 2. | tan(12) =
108/lengte hemelsbreed lengte hemelsbreed = 108/tan(12) = 508 meter |
||
| 3. |
|
||
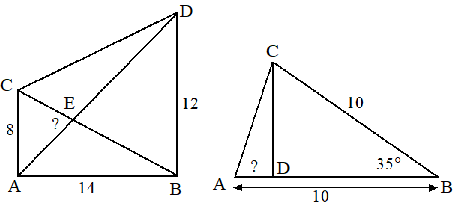
| a, | tan(ACB) = 14/8
geeft ∠ACB = 60,25° tan(ADB) = 14/12 geeft ∠ADB = 49,40° dus dan is ∠BAD = 40,60° en dan is ∠CAD = 49,40° Dan is ∠CEA = 180° - 60,25° - 49,40° = 70,35°. |
||
| b. | sin(35) = CD/10
geeft CD = 10sin(35) = 5,74 Teken BE loodrecht op AC Dan is sin(17,5) = AE/10 dus AE =3,01 AC = 6,02 AD2 = 6,022 - 5,742 geeft AD = 1,81 |
||
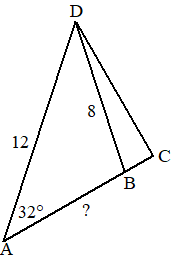
| 4. | Verleng AB tot
AC zodat AC loodrecht op DC staat. sin(32) = DC/12 dus DC = 12sin(32) = 6,359 cos(32) = AC/12 dus AC = 12cos(32) = 10,177 Pyhthagoras: BC2 = 82 - 6,3592 dus BC = 4,854 AB = 10,177 - 4,854 = 5,323 |
|
|
| 5. | Noem de hoogte
van de toren x Landmeter A: tan(68) = x/afstand tot de toren Dus afstand tot de toren = x/tan(68) Op dezelfde manier geldt voor landmeter B: afstand tot de toren = x/tan(78) x/tan(68) + x/tan(78) = 60 Dat geeft x = 97,3 meter |
||