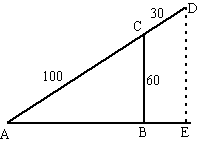© h.hofstede (h.hofstede@hogeland.nl)
     
1. a. x2 = 102 + 142 - 2 • 10 • 14 • cos52º  = 123,61  ⇒  x = √123,61 = 11,1
       
  b. 152 = 72 + 112 - 2 • 7 • 11 • cosα
225 = 170 - 154cosα
55 = -154cosα
cosα = -0,357
α = 110,9º
       
  c. 92 = 102 + 62 - 2 • 10 • 6 • cosα
81 = 136 - 120cosα
-55 = -120cosα
cosα = 0,458
α = 62,7º
       
  d. x2 = 42 + 92 - 2 • 4 • 9 • cos71 = 73,56  ⇒  x = √73,56 = 8,6
       
2.  

     
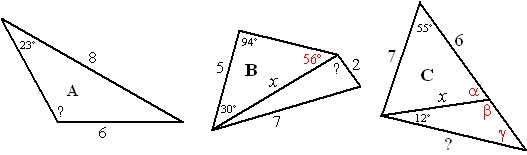
  a. 6/sin23 = 8/sinα
sinα = 8 • sin23/6 = 0,521
α = 31,4º  maar je moet de hoek  180 - 31,4 = 148,6º hebben
       
  b. 5/sin56 = x/sin94
x = sin94 • 5/sin56 = 6,016

72 = 22 + 6,0162 - 2 • 2 • 6,016 • cosα
49 = 40,197 - 24,066 • cosα
8,803 = - 24,066 • cosα
cosα = -0,366
α = 111,5º 
       
  c. x2 = 62 + 72 - 2 • 6 • 7 • cos55 = 36,82  Þ  x = √36,82 = 6,07

7/sinα = x/sin55
sinα = 7 • sin55/6,07 = 0,945
α = 70,90º
dan is  β = 109,09º  en  γ = 58,91º
7/sinγ = ?/sin55
? = sin55 • 7/sin58,91 = 6,7
       
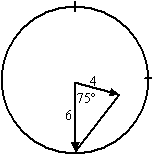
3. De hoek is dan 75º.

x2 = 42 + 62 - 2 • 4 • 6 • cos75 = 39,58
x = √39,58 = 6,29 cm

4. voor de hoek bij A geldt:  72 = 92 + 32 - 2 • 9 • 3 • cosα
49 = 90 - 54cosα
-41 = -54cosα
cosα = 0,759
α = 40,6º

sin(40,6) = CD/3
CD = 3 • sin40,6 = 1,95
       
5. ∠BQA = 180 - 28 - 47 - 38 = 67º
driehoek BQA:  600/sin67 = AQ/sin85  ⇒   AQ = sin85 • 600/sin67 = 649,34

∠APB = 180 - 22 - 28 - 47 = 83º
driehoek APB:  600/sin83 = AP/sin47 ⇒ AP = sin47 • 600/sin83 = 442,11

driehoek PQA:  PQ2 = 442,112 + 649,342 - 2 • 442,11 • 649,34 • cos22 = 84751,13
Dan is PQ = √84751,13 = 291 meter
       
       
6. a. D heeft maximale hoogte als B recht onder C staat.

ABC en AED zijn gelijkvormig
BC/CA = DE/DA
60/100 = DE/130
DE = 130 • 60/100 = 78 cm hoog

       
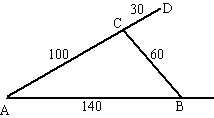
  b. De situatie is dan als hiernaast.
Helemaal ingeklapt was AB = 160, dus nu is AB = 140

602 = 1002 + 1402 - 2 • 100 • 140 • cosα
3600 = 29600 - 28000 • cosα
-26000 = -28000•cosα
cosα = 0,928
α = 21,79º en dat is hoek BAC.

sin(21,79) = hoogteD/130
hoogte D = 130 • sin(21,79) = 48,2 cm gaat D omhoog

       
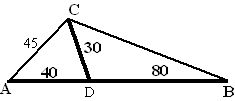
7. in driehoek ACD:

302 = 402 + 452 - 2 • 40 • 45 • cosα
900 = 3625 - 3600 • cosα
-2725 = -3600cosα
cosα = 0,757
α = 40,80º

in driehoek ACB:
BC2 = 452 + 1202 - 2 • 45 • 120 • cosα
BC2 = 8250
BC = 90,8 meter

       
8. Cosinusregel:
922 = 1012 + 1452 - 2 · 101 · 145 cos(C)
8464 = 10201 + 21025 - 29290cos(C)
-22762 = -29290cos(C)
cos(C) = 0,7771....
C = 39,00...

Teken de hoogtelijn BD vanuit B loodrecht op  AC
sin(39,00...) = BD/101  geeft  BD = 63,56....

De oppervlakte is dan  0,5 · 63,56 · 145 = 4608 m2
       
9. a. AS = 0,5AC = 7,5
BS = 0,5BD = 5
cosinusregel in ABS:
52 = 122 + 7,52 - 2 · 5 · 7,5 cos(BAC)
25 = 144 + 56,25 - 180cos(BAC)
-175,25 = -180cos(BAC)
cos(BAC) = 175,25/180 = 0,9736....
BAC = cos-1(0,9736...) = 13,1919...
       
  b. cosinusregel in ABC:
BC2 = 122 + 152 - 2 · 12 ·15 · cos(13,2)
BC2 = 18,5
BC = 4,30
       
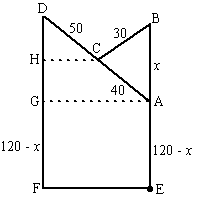
10. Als AB = x dan is  AE = 120 - x

driehoek ABC:
302 = 402 + x2 - 2 • 40 • x • cos∠CAB
80x • cos∠(CAB) = 700 + x2
cos∠CAB = (700 + x²)/80x

  maar dat is ook cos∠ADG  want die hoeken zijn gelijk (Z-hoeken)

in driehoek AGD:  cos∠ADG = DG/90 ⇒ DG = 90 • cos∠ADG

dat geeft DG = 90 • (700 + x²)/80x = 787,5/x + 9/8x
DF = h = DG + GF =   787,5/x + 9/8x + 120 - x  = 787,5/x + 1/8x + 120
       
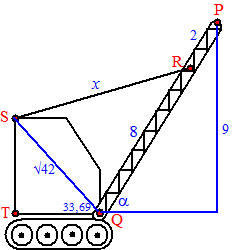
11. SQ2 = 62 + 42  dus  SQ = √42

tan (SQT) = (4/6)  geeft  ∠SQT = 33,69º

sinα = 9/10  geeft  α =  64,16º

Dan is ∠SQR = 180 - 33,69 - 64,16 = 82,15º

cosinusregel:  x2 = 42 + 64 - 2 • √42 • 8 • cos82,15
x2 = 92,45
x = 9,62 m

       
12. zie de schets hiernaast.

cosinusregel:
x2 = 82 + 92,582 - 2 • 8 • 92,58 • cos(28,65)
x2 = 7335,137
x = 85,65

Het verschil is 107 cm
       
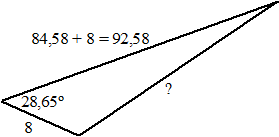13. a. cosinusregel in driehoek M1M2M3;
(r + 2)2 = (r + 6)2 + 82 - 2 • (r + 6) • 8 • cos(M1M2M3)
r2 + 4r + 4 = r2 + 12r + 36 + 64 - (16r + 96) • cos(M1M2M3)
-8r - 96 =  -(16r + 96) • cos(M1M2M3)
delen door -8:    r + 12 = (2r + 12)cos(M1M2M3)
cos(M1M2M3) = (r + 12)/(2r + 12)
       
  b. Als r naar oneindig nadert, dan nadert de cosinus tot 1/2.
Dan nadert de hoek naar 60º
       
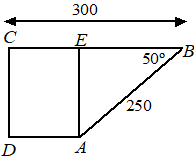
14. a. Teken lijnstuk AE loodrecht op BC.
cos50º = EB/250
EB = 250 • cos50º = 160,69...
AD = BC - EB = 300 - 160,69... = 139,30...
Dat is inderdaad ongeveer 139 cm.

       
  b. Pythagoras:  AC2 = 1392 + 2922 = 104585  dus  AC = √104585 = 323,396....
Cosinusregel in driehoek ABC:
323,396...2 = 3002 + 2502 - 2 • 300 • 250 • cosα
104585 = 152500 - 150000cosα
150000cosα = 47915
cosα = 0,3194...
α = 71,37...º
Het is dus 71,37... - 50 = 21º toegenomen.
       
15. tweemaal de cosinusregel:
s2 = p2 + q2 - 2pqcos(β)
r2 = p2 + q2 - 2pqcos(α)

maar α + β + 2 • 90 º = 360º  dus  β = 180º - α
dan is  cos(β) = cos(180º - α) = -cosα
de eerste cosinusregel geeft dan  s2 = p2 + q2 + 2pqcosα

tel nu beide vergelijkingen bij elkaar op:  r2 + s2 = 2(p2 + q2 )
p2 + q2 = 1/2(r2 + s2)
links staat de oppervlakte van de lichtpaarse vierkanten, rechts staat de helft van de oppervlakte van de donkerpaarse vierkanten......
       
16. 82 = 52 + 112 - 2 • 5 • 11 • cosA
64 = 146 - 110cosA
-82 = -110cosA
cosA = 0,74545...
A = 41,8018...º

cosA = AD/5  dus  0,74545... = AD/5  dus  AD = 5 • 0,74545... = 3,727...
De driehoeken ADE en ABC zijn gelijkvormig  (F-hoeken)
 
AD
3,727...		 DE
??		 AE
 
AB
11		 BC
8		 AC
 
  DE = 8 • 3,727.../11 = 2,71
       
17. Noem de tophoek α
Dan geldt in de bovenste driehoek:  32 = 42 - 2 • 3 • 4 • cosα  dus  cosα = 11/16

In de hele driehoek:   x2 = 82 + 112 - 2 • 8 •11 • cos α = 64
Dus x = 8
       
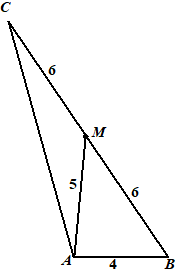
18. cosinusregel in ABM:
52  = 42 + 62 - 2 • 4 • 6 • cosB
25 = 52 - 48cosB
48cosB = 27
cosB = 27/48
B = 55,77113...

cosinusregel in ABC
AC2 = 42 + 122 - 2 • 4 • 12 • cos(55,77113...)
AC2 = 160 - 96 • 27/48
AC2 = 106
AC = √106 = 10,3

       
19. cosinusregel:  BF2 = 5422 + 4252 - 2 • 542 • 425 • cos(58)
Dat geeft  ∠BF = 479,849...

sinusregel:  479,849/sin(58) = 542/sin(∠BAF)
dat geeft  sin(∠BAF) = 0,957...
Dan is ∠BAF = 73,31° 
Dat scheelt afgerond 2°
       
20.

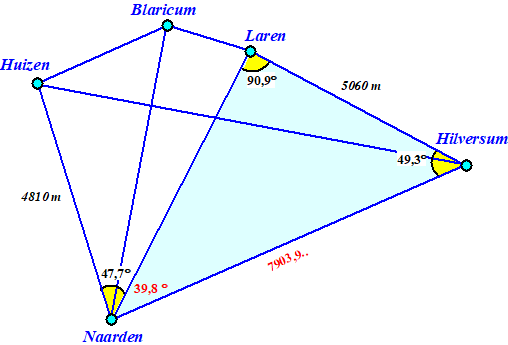
  Bekijk eerst de lichtblauwe driehoek:
De hoek tussen  Hilversum-Naarden-Laren  is 180 - 90,9 - 49,3 = 39,8°
Sinusregel:   HN/sin(90,9) = 5060/sin39,8
Dat geeft HN = 7903,9...
Gebruik nu de cosinusregel in de driehoek Huizen-Hilversum-Naarden:

x2 = 48102  + 7903,92 - 2 • 4810 • 7903,9 • cos(39,8 + 47,7)
Dat geeft  x =  9070 meter.
       
21. cosinusregel in BCQ:  122  = 72 + 72 - 2 · 7 · 7 · cos(2a)
144 = 98 - 98cos(2a)
46 = -98cos(2a)
cos(2a) = -0,4693.....
2a = 118
a = 59

cosinusregel in driehoek ABC:  122 = 102 + AC2 - 2 · 10 · AC · cos(59)
144 = 100 + AC2 - 10.30 · AC
AC2 - 10,30AC - 44 = 0
de ABC-formule geeft AC = 13,549...
afgerond is AC = 13,55
       
22. In de oorspronkelijke (niet-gekantelde) figuur is 
AE2 = 0,252 + 0,302 = 0,1525
Dus AE = √0,1525 = 0,39...

BE2 = 1,802 + 0,252 = 3,3025
Dus  BE = √3,3025 = 1,817...

In de gekantelde situatie kun je nu de cosinusregel in driehoek ABE gebruiken:
1,602 = 0,392  + 1,8172 - 2·0,39·1,817·cos(∠AEB)
1,602 = 3,45 - 1,42·cos(∠AEB)
-0,89 = -1,42 ·cos(∠AEB)
cos(∠AEB) = 0,625
∠AEB = 50,9°

Niet-gekantelde situatie:  tan(∠BED) = 0,25/1,8  dus  ∠BED = 7,9°

∠AED is nu 50,9 + 7,9 = 58,8°
Dat was oorspronkelijk 39,8°
De bak is dus  58,8 - 39,8 = 19,0° gekanteld.