|
|||||
 |
|||||
| 1. | a. | 88 is 2σ onder de 120 dus links daarvan zit 2,5% | |||
| b. | 136 is σ boven de 120 dus rechts daarvan zit 13,5 + 2,5 = 16% | ||||
| c. | 104 is σ onder de 120 dus rechts daarvan zit 34 + 34 + 13,2 + 2,5 = 84% | ||||
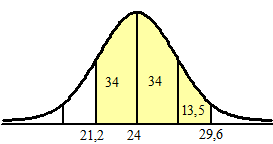
| 2. | a. | 34 + 34 + 13,5 = 81,5% |
|
||
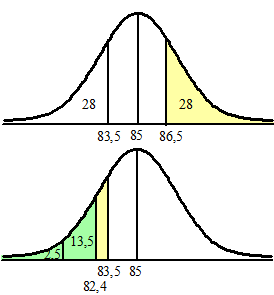
| b. | bovenste figuur: onder de 83,5 zit 28% onderste figuur: groen + geel = 28 Dus geel = 28 - 13,5 - 2,5 = 12% |
|
|||
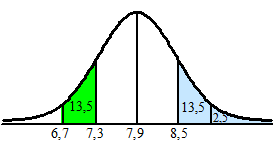
| c. |
s = 0,6 boven de 8,5: 13,5 + 2,5 = 16% |
|
|||
| 3. | a. | 68% is tussen
m + s en
m -
s Dus bij de vuistregels geeft dat m = 133 en s = 3 |
|||
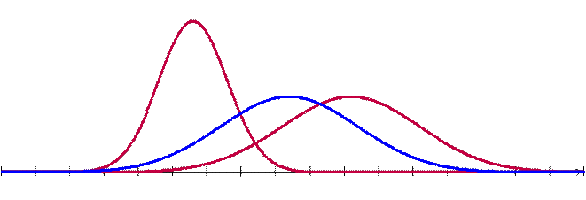
| b. | Er zijn veel meer gebieden onder een klokvorm te vinden die 68% van de oppervlakte zijn. Dus als dat gebied ergens anders ligt krijg je ook een andere m en andere s (die kun je alleen niet berekenen omdat dat niet bij de vuistregels past). | ||||
| 4. | a. |
Het
midden bij 234
? |
|||
|
|
|||||
| b. |
206 en 226
is het gemiddelde en het gemiddelde plus tweemaal de standaardafwijking Daartussen zit 47,5% |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||