fouten van de tweede soort

© h.hofstede (h.hofstede@hogeland.nl)

Fouten van de eerste en van de tweede soort.

Tot nu toe hadden we het bij het aannemen of verwerpen van H₀ steeds over de kans op een foute conclusie. Maar dat was steeds alleen maar de kans dat H₀ ten onrechte werd verworpen. Die vergeleken we met α.

Maar eigenlijk zijn er natuurlijk bij elke toets VIER mogelijkheden:

		beslissing
		H₀ wordt aangenomen	H₀ wordt verworpen
werkelijkheid	H₀ is waar	GOED	FOUT
werkelijkheid	H₀ is niet waar	FOUT	GOED

Twee van de vier opties geven zoals je ziet een foute conclusie, de andere twee een kloppende conclusie.
Tot nu toe hebben we het alleen maar gehad over die bovenste twee, met kansen α (significantieniveau) en 1 - α (betrouwbaarheidsniveau).

		beslissing
		H₀ wordt aangenomen	H₀ wordt verworpen
werkelijkheid	H₀ is waar	(1 - α)	α
werkelijkheid	H₀ is niet waar

Die rode fout om H₀ te verwerpen terwijl H₀ WAAR is, heet een "fout van de eerste soort", en die gaven we aan met α.
Dat andere rode vakje heet een "fout van de tweede soort". Dat is dus de fout dat H₀ ten onrechte wordt aangenomen. Die geven we vanaf nu aan met β.

Die onderste rij, daar kwamen we niet aan toe, vooral omdat H₁ niet een bewering deed als μ = .... of p = ....
En H₁ zei altijd iets veel vagers als μ > ... of p < ... of zoiets
En tja, als je niet weet welke kansverdeling H₁ nou precies beweert, dan kun je ook niet de kans uitrekenen dat H₁ ten onrechte verworpen wordt. Je hebt immers geen klokvorm om aan te rekenen. 't Was meer uit armoede dus dat we het nooit over die fout van de tweede soort hebben gehad.

Tijd om dat te veranderen.......

Laten we eens een geval nemen waarin H₁ wél een precieze bewering doet.

Het voorbeeld van de valse dobbelstenen.

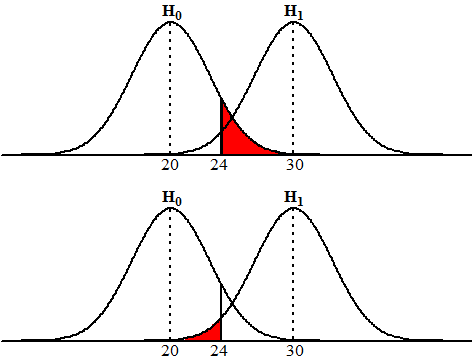
Bij een zuivere dobbelsteen is de kans om 6 te gooien gelijk aan ¹/₆. Dat weet iedereen. Stel nu dat er valse dobbelstenen in omloop zijn waarbij de kans op een 6 gelijk is aan ¹/₄.
Jij hebt een dobbelsteen voor je neus liggen en wilt bepalen of het zo'n valse is of een zuivere.
Je gooit 120 keer en vindt 24 zessen.
Wat is je conclusie?
Wat is de kans op een foute conclusie?

Laten we eerst vaststellen dat H₀ en H₁ hier twee precieze beweringen zijn:
H₀: P(6) = ¹/₆ (het is een zuivere dobbelsteen)
H₁: P(6) = ¹/₄ (het is een valse dobbelsteen)

Van de 120 keer gooien verwacht H₀ dus 20 zessen en H₁ verwacht 30 zessen.
Daar horen deze twee plaatjes bij:

Als je besluit H₀ te verwerpen geeft de bovenste rode oppervlakte de fout die je dan eventueel maakt (fout van de eerste soort), namelijk dat H₀ wel waar is, maar je meting toch minstens 24 opleverde.
Als je besluit H₁ te verwerpen dan geeft de onderste rode oppervlakte de fout die je dan eventueel maakt (fout van de tweede soort) namelijk de kans dat H₁ waar is, maar je meting toch hoogstens 24 opleverde.

Dat geeft dus α = 1 - binomcdf(120, ¹/₆, 23) = 0,1935 en β = binomcdf(120, ¹/₄, 24) = 0,0391

Die tweede fout is kleiner dan die eerste, dus H₁ maar verwerpen dus?

Was het leven maar zo simpel...
Was het leven maar gewoon wiskunde....!

Helaas komen er meestal allerlei andere zaken bij kijken. Bijvoorbeeld: het maken van beide fouten is vaak niet even rampzalig. Neem een geval waarin een jury moet beslissen om iemand te veroordelen of vrij te spreken aan de hand van het aanwezige bewijsmateriaal. Als je neemt H₀ = hij is onschuldig (of zij natuurlijk: sorry dames!) en H₁ = hij is schuldig, dan betekent een fout van de eerste soort dat je een onschuldig iemand veroordeelt, en een fout van de tweede soort betekent dat je een schuldig iemand vrijspreekt.
Meestal vindt men in de rechtspraak de eerste fout veel zwaarder wegen dan de tweede ("guilt must be proved beyond all reasonable doubt").
Als je wiskundig maar inziet dat er geen manier is om beide fouten (α en β) tegelijk te verkleinen. Als je α kleiner wilt maken moet je in bovenstaand voorbeeld de grenswaarde G van H₀ aannemen/verwerpen naar links verschuiven, maar dan wordt automatisch β groter. En andersom.

De enige manier om α én β tegelijk te verkleinen is meer experimenten te doen! Immers als n groter wordt dan worden beide verdelingen smaller (meer rondom hun midden geconcentreerd) en dus α én β kleiner!