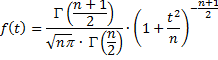© h.hofstede (h.hofstede@hogeland.nl)

De t-verdeling.
 
Bij het nemen van een steekproef gingen we in de vorige les steeds uit van een normale verdeling in een hele populatie.
We vonden dan een bepaald gemiddelde in onze steekproef en probeerden daar conclusies uit te trekken over het gemiddelde in de hele populatie. Dat werden dan betrouwbaarheidsintervallen.

Bij de berekeningen van die betrouwbaarheidsintervallen hadden we de standaarddeviatie (σ) nodig.

Maar een erg zwak punt in het verhaal daarbij is, dat we die standaarddeviatie van de hele populatie helemaal niet kennen! (Die kun je alleen vinden door de hele populatie te meten, en tja, dan is het geen statistiek meer..... dan is het gewoon de absolute waarheid....Bah! Stel je voor zeg!!)

We namen dan uit nood maar gewoon de standaarddeviatie van onze steekproef, en maakten de aanname (hoop?) dat de standaarddeviatie van de hele populatie daar wel gelijk aan zou zijn.
Die aanname klopt natuurlijk niet!
       

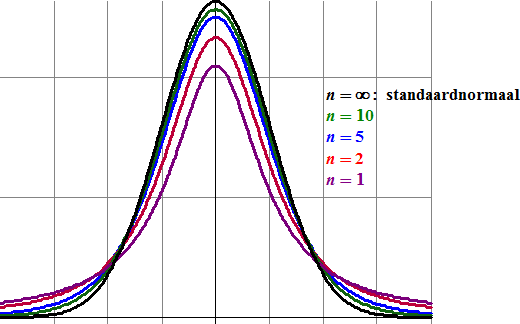
De standaarddeviatie van de populatie is niet gelijk aan de standaarddeviatie van de steekproef!
       
Ik hoop dat je aanvoelt dat de standaarddeviatie van je steekproef groter zal zijn dan de standaarddeviatie van de hele populatie. Het betekent dat de   z = (X - μ)/σ  van de standaardnormale verdeling  nu verandert in  t = (X - μ)/s  waarbij die s de standaarddeviatie van je steekproef is. Maar die s hangt wel af van de steekproefgrootte n, dus dat betekent dat je voor elke steekproefgrootte n een andere verdeling voor  t  krijgt. Die verdelingen zijn niet meer gelijk aan een standaardnormale verdeling alhoewel ze er wel op lijken. Hieronder zie je een aantal zulke t-verdelingen.
       

       
Zoals je ziet zijn de staarten van de verdeling wat groter dan bij de normale verdeling, en dat is maar goed ook:  bij een kleinere steekproef verwachten we natuurlijk een grotere kans op uitschieters. Voor n steeds groter nadert de t-verdeling de standaardnormale verdeling (de zwarte hierboven) Je ziet dat dat trouwens best snel gebeurt:  vanaf n = 50 is de t-verdeling haast niet meer te onderscheiden van de standaardnormale verdeling.
De formule van de t-verdeling is er eentje om niet al te lang te onthouden:
       

       
Die Γ is de gammafunctie, en je ziet dat er inderdaad een n als parameter in voorkomt. Voor elke n een andere t-verdeling. (In veel statistiekboeken zie je trouwens dat in plaats van n wordt gewerkt met  df = n - 1, waarin df staat voor  "degrees of freedom":  het aantal vrijheidsgraden)

Ik ken eigenlijk weinig wiskundigen die deze formule actief gebruiken (hoogstens misschien om anderen mee te imponeren). Iedereen gebruikt eigenlijk alleen maar de tabellen voor de t-waarden die bij allerlei n aangeven waar de oppervlakte  10%, 5%, 1% enz. is. Die heb je immers nodig om de betrouwbaarheidsintervallen te berekenen.
Hier is 'íe:
 

kans
n 0,25 0,10 0,05 0,025 0,010 0,005 0,001
2
3
4
5		 1,000
0,816
0,765
0,741		 3,078
1,886
1,638
1,533		 6,314
2,920
2,353
2,132		 12,706
4,303
3,182
2,776		 31,821
6,965
4,541
3,747		 63,675
9,925
5,841
4,604		 318,31
22,326
10,213
7,173
6
7
8
9
10		 0,727
0,718
0,711
0,706
0,703		 1,476
1,440
1,415
1,397
1,383		 2,015
1,943
1,895
1,860
1,833		 2,571
2,447
2,365
2,306
2,262		 3,365
3,143
2,998
2,896
2,821		 4,032
3,707
3,499
3,355
3,250		 5,893
5,208
4,785
4,501
4,297
11
12
13
14
15		 0,700
0,697
0,695
0,694
0,602		 1,372
1,363
1,356
1,350
1,345		 1,812
1,796
1,782
1,771
1,761		 2,228
2,201
2,179
2,160
2,145		 2,764
2,718
2,681
2,650
2,624		 3,169
3,106
3,055
3,012
2,977		 4,144
4,025
3,930
3,852
3,787
16
17
18
19
20		 0,691
0,690
0,689
0,688
0,688		 1,341
1,337
1,333
1,330
1,328		 1,753
1,746
1,740
1,734
1,729		 2,131
2,120
2,110
2,101
2,093		 2,602
2,583
2,567
2,552
2,539		 2,947
2,921
2,898
2,878
2,861		 3,733
3,686
3,646
3,610
3,579
21
22
23
24
25		 0,687
0,686
0,686
0,685
0,685		 1,325
1,323
1,321
1,319
1,318		 1,725
1,721
1,717
1,714
1,711		 2,086
2,080
2,074
2,069
2,064		 2,528
2,518
2,508
2,500
2,492		 2,845
2,831
2,819
2,807
2,797		 3,552
3,527
3,505
3,485
3,467
26
27
28
29
30		 0,684
0,684
0,684
0,683
0,683		 1,316
1,315
1,314
1,313
1,311		 1,708
1,706
1,703
1,701
1,699		 2,060
2,056
2,052
2,048
2,045		 2,485
2,479
2,473
2,467
2,462		 2,787
2,779
2,771
2,763
2,756		 3,450
3,435
3,421
3,408
3,467
40
60
120		 0,681
0,679
0,677		 1,303
1,296
1,289		 1,684
1,671
1,658		 2,021
2,000
1,980		 2,423
2,390
2,358		 2,704
2,660
2,617		 3,307
3,232
3,160
∞ 0,674 1,282 1,645 1,960 2,326 2,576 3,090
       
Die laatste rij geeft dus de z-waarden van de standaardnormale verdeling.

Voorbeeld
Ik heb een mini-onderzoekje gedaan onder 10 kinderen van groep 8, waarin ik ze heb laten bijhouden hoeveel minuten ze per dag achter de computer zaten.
Dat leverde op:  125 - 58 - 15 - 235 - 156 - 88 - 166 - 210 - 142 - 52
Dat geeft een gemiddelde van  90,7  met een standaarddeviatie van 66,45
Dus voor het gemiddelde van 10 metingen is  σ = 66,45/√10 = 21,01
Ik wil graag een 95%-betrouwbaarheidsinterval voor het gemiddelde van alle groep-8 kinderen in Nederland opstellen. 
• Met de standaardnormale verdeling zou ik vinden  z = ±1,960  dus  μ = 90,7 ± 1,96 • 21,01
Het 95%-betrouwbaarheidsinterval wordt  [58.5, 132.9]
• Met de t-verdeling voor n = 10 vind ik  t = ±2,262 dus  μ = 90,7 ± 2,262 • 21,01
Het 95%-betrouwbaarheidsinterval wordt  [43.2, 138.2]
Je ziet: het scheelt nogal. Die laatste is uiteraard de goede.
       
Als de steekproefgrootte toeneemt wordt de nauwkeurigheid groter (de breedte van het betrouwbaarheidsinterval dus kleiner), en dat is dus vanwege twee redenen:
  1. de standaarddeviatie wordt gedeeld door √n
  2. de kritieke waarde voor t wordt kleiner als n groter wordt.
       
       
   OPGAVEN
       
1.  
       
       
       

© h.hofstede (h.hofstede@hogeland.nl)