| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
 |
|
Grafieken veranderen |
| |
|
|
|
In deze les over
parabool grafieken hebben we al drie manieren besproken over het
veranderen van een functievoorschrift en wat dat voor gevolgen voor de
grafiek heeft.
Laten we ze nog even samenvatten: |
| |
|
|
|
|
grafiek a
omhoog schuiven ⇒ f(x) wordt
f(x) + a |
|
| |
|
|
|
|
grafiek
a naar rechts schuiven
⇒ elke x
vervangen door (x -
a) |
|
| |
|
|
|
|
afstand tot de x-as a keer zo groot
⇒
vermenigvuldig de hele formule met a |
|
| |
|
|
|
De eerste twee heten
translaties (verschuivingen) en de derde heet een vermenigvuldiging.
· En als je bij de eerste f(x)
vervangt door f(x) - a dan gaat de grafiek
uiteraard omlaag.
· En als je bij de tweede x
vervangt door (x + a) dan gaat de grafiek uiteraard naar
links.
· En als je bij de derde een a
neemt die kleiner is dan 1 dan wordt de afstand tot de x-as
uiteraard kleiner.
Zo, zijn we helemaal weer bijgepraat.
Deze les gaan we er drie transformaties aan toevoegen. |
| |
|
|
|
|
1. Spiegelen in de x-as. |
| |
|
|
 |
| Dan klapt de hele grafiek als het ware om. Dat betekent dat elke y
tegengesteld wordt (plus wordt min en min wordt plus). In de
formule kunnen we dat bereiken door een minteken voor de hele formule te
zetten (want de hele formule, dat is immers de y).
|
| |
|
|
|
spiegelen
in de x-as
⇒
minteken voor de hele formule |
|
| |
|
|
|
|
2. Spiegelen in de
y-as. |
| |
|
|
|
Dat betekent dat punten rechts van de
y-as
naar links gaan en andersom.
Dus worden negatieve x-en positief
en positieve x-en negatief.
In feite wisselt elke x van
teken. Dat betekent voor de formule:
|
| |
|
|
|
|
spiegelen in de y -as ⇒
vervang elke
x door -x |
|
| |
|
|
|
|
3. Vermenigvuldigen
ten opzichte van de y-as. |
| |
|
|
|
Dat is een lastige......
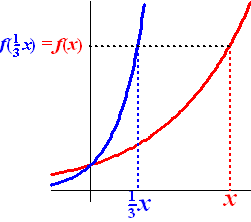
Hiernaast zie je twee grafieken. De rode is verkregen door de blauwe te
vermenigvuldigen t.o.v. de y-as met factor 3 (dus elk punt is
drie keer zo ver van de y-as afgekomen).
Als we op zoek zijn naar f(x)
(dat is de y van de nieuwe
formule) dan zie je hiernaast dat die gelijk is aan de y
van de oude formule die hoort bij
1/3x.
En wat voor het getal 3 geldt geldt natuurlijk ook voor een
willekeurige a.
Conclusie: |
|
| |
|
|
|
|
afstand
tot de y -as a keer zo groot
⇒
vervang elke x
door (1/a
• x) |
|
| |
|
|
|
Tijd Voor Goed Nieuws!!!
We hebben nu zes mogelijke transformaties van grafieken
bekeken.
Het goede nieuws is: Daar komt niks meer bij!!!!
Tot en met je eindexamen HAVO wiskunde B is dit alles wat je moet weten
over transformaties.
Altijd prettig een onderdeel af te sluiten toch?
Hier zijn ze nog een keer alle zes: |
| |
|
|
|
| grafiek a
omhoog schuiven |
⇒ f(x) wordt
f(x) + a |
| grafiek
a naar rechts schuiven |
⇒ elke x
vervangen door (x -
a) |
| afstand tot de x-as a
keer zo groot |
⇒
vermenigvuldig de hele formule met a |
| afstand
tot de y -as a keer zo groot |
⇒
vervang elke x
door (1/a
• x) |
| spiegelen
in de x-as |
⇒
minteken voor de hele formule |
| spiegelen in
de y -as |
⇒
vervang elke
x door -x |
|
|
| |
|
|
|
Voorbeeld
met een wortelgrafiek:
Schets de grafiek van y = 6 -
2√(0,5x + 4) en geef het domein en het bereik..
Laten we een stripverhaal gaan maken: |
| |
|
|
|
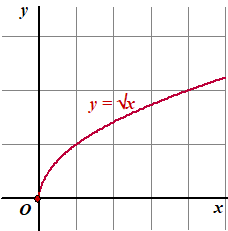
| 1. |
Begin met de grafiek
van y = √x
Die moet je gewoon uit je hoofd leren: we beschouwen dat als
een standaardgrafiek. |
 |
| 2. |
Vervang x door
(x + 4)
Dat betekent dat de grafiek 4 naar links wordt geschoven
De formule wordt dan y = √(x + 4) |
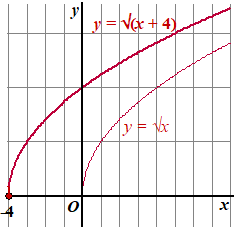 |
| |
|
|
|
| 3. |
Vervang elke x
door 0,5x
Dat betekent dat de afstand tot de y-as 1/0,5
= 2 keer zo groot wordt.
De formule wordt dan y = √(0,5x + 4) |
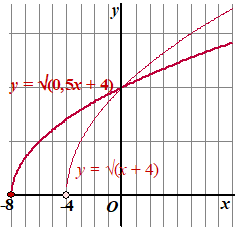 |
| 4. |
Vermenigvuldig de
hele formule met 2.
Dat betekent dat de afstand tot de x-as dubbel zo groot wordt
gemaakt.
De formule wordt dan y = 2√(0,5x + 4) |
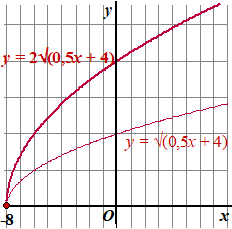 |
| 5. |
Zet een minteken voor
de hele formule
Dat betekent dat de grafiek wordt gespiegeld in de x-as
De formule wordt dan y = -2√(0,5x + 4) |
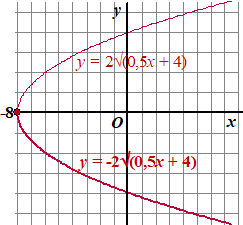 |
| 6. |
Zet +6 bij de
hele formule (ervoor of erachter dat maakt niet uit)
Dat betekent dat de grafiek 6 omhoog wordt geschoven
De formule wordt dan eindelijk y = 6 -
2√(0,5x + 4) |
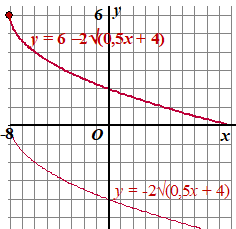 |
| |
|
|
|
De schets zie je
hierboven.
Daaruit kun je direct aflezen dat het randpunt (-8, 6) is en het
domein [-8, →〉 en het bereik 〈←,
6] |
| |
|
|
|
|
De volgorde.... |
| |
|
|
|
De volgorde waarin je
bovenstaande stappen uitvoert kan wel gevolgen voor de grafiek hebben,
maar het hoeft niet altijd.
Dat klinkt nogal vaag, maar ik zou er geen regels voor gaan leren. Kijk
gewoon of je op de goede formule uitkomt.
Als je bijvoorbeeld in het voorbeeld hierboven stap 2 en stap 3
verwisselt gaat het fout.
Kijk maar:
GOED:
Vervang x door (x + 4) geeft y = √(x
+ 4)
Vervang daarna x door 0,5x geeft y
= √(0,5x + 4)
FOUT:
Vervang x door 0,5x geeft y = √(0,5x)
Vervang daarna x door (x + 4) geeft y
= √(0,5(x + 4)) = √(0,5x + 2)
Maar stap 4 en stap 5 mag je best met elkaar verwisselen.
Ga zelf maar na dat dat wel de goede formule oplevert. |
| |
|
|
|
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
Schets de grafieken van de volgende
functies en leg uit via welke transformaties (en in welke
volgorde) zij zijn ontstaan uit een basisgrafiek.
Geef het domein en het bereik. |
| |
|
|
|
| |
a. |
y = 8 - √(x
- 2) |
|
| |
|
|
|
| |
b. |
y = √(4x
- 12) |
|
| |
|
|
|
| |
c. |
f(x) = 3(8
- x)2
- 5 |
|
| |
|
|
|
| 2. |
a. |
De grafiek van y =
√x
wordt 3 omlaag geschoven en 4 naar rechts. Daarna wordt de
afstand tot de x-as gehalveerd. Geef een
functievoorschrift van de grafiek die dan is ontstaan. |
| |
|
|
|
| |
b. |
De grafiek van y = x2
wordt gespiegeld in de x-as. Daarna wordt hij 2 omlaag
geschoven en tenslotte wordt de afstand tot de y-as twee
keer zo groot gemaakt. Geef een functievoorschrift van de
grafiek die dan is ontstaan. |
| |
|
|
|
| 3. |
Bekijk de volgende vier
transformaties: |
| |
| A: |
spiegelen in de x-as |
| B: |
afstand tot de y-as verdubbelen |
| C: |
2 naar links schuiven |
| D: |
5 omhoog schuiven |
|
| |
|
|
|
| |
Van welke van deze transformaties doet
de volgorde er niet toe en van welke wél? |
| |
|
|
|
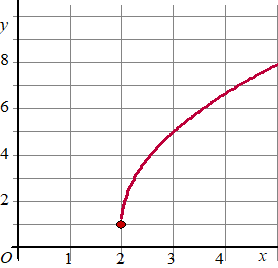
| 4. |
Hiernaast zie je de
grafiek van
y = a + b√(x + c)
Bepaal uit deze grafiek de waarden van a, b en c |
 |
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|