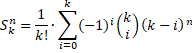© h.hofstede (h.hofstede@hogeland.nl)

Stirling Getallen.
-van de tweede soort-
       
Deze les bespreken we Stirling-getallen van de tweede soort. (er zijn ook Stirling-getallen van de eerste soort, die staan in deze les).

Geen inleiding of zo,  meteen maar naar de hoofdvraag:

"Op hoeveel manieren kun je een verzameling van n getallen verdelen in k niet-overlappende, niet-lege deelverzamelingen?"
of ook wel:  hoeveel partities van k deelverzamelingen heeft een verzameling met n elementen?

Dat aantal noemen we het Stirling-getal Snk  

Snel voorbeeldje:   de verzameling  {a, b, c} kun je onderverdelen in twee deelverzamelingen als:
{a}{b, c}
{b}{a, c}
{c}{a, b}
Dus  S32 =  3

Langzamer voorbeeldje:  de verzameling  {a, b, c, d}  kun je onderverdelen in twee deelverzamelingen als:
{a}{b, c, d}
{b}{a, c, d}
{c}{a, b, d}
{d}{a, b, c}
{a, b}{c, d}
{a, c}{b, d}
{a, d}{b, c}
Dus  S42 = 7
       
Een tabel van deze Stirling-getallen ziet er zó uit:
       

Skn

 k
1 2 3 4 5 6 7 8 9 10
   n    1 1 0 0 0 0 0 0 0 0 0
2 1 1 0 0 0 0 0 0 0 0
3 1 3 1 0 0 0 0 0 0 0
4 1 7 6 1 0 0 0 0 0 0
5 1 15 25 10 1 0 0 0 0 0
6 1 31 90 65 15 1 0 0 0 0
7 1 63 301 350 140 21 1 0 0 0
8 1 127 966 1701 1050 266 28 1 0 0
9 1 255 3025 7770 6951 2616 462 36 1 0
10 1 511 9330 34105 42525 22827 5880 750 45 1
       
Voor kleinere aantallen zijn de getallen nog wel te beredeneren.

slim voorbeeldje
voor S53 kun je zien dat de deelverzamelingen grootte  3-1-1 of 2-2-1 moeten hebben
voor 3-1-1 heb je  (5 nCr 3) = 10 mogelijkheden om de verzameling van 3 te kiezen.
voor 2-2-1 heb je 5 mogelijkheden voor de verzameling van 1, en daarna nog 3 mogelijkheden om de overgebleven 4 elementen in twee verzamelingen van 2 te verdelen. Immers je kunt 2 kiezen op (4 nCr 2) = 6 manieren, maar dan tel je ze allemaal dubbel want {a, b} kiezen geeft dezelfde verdeling als  {c, d} kiezen..
In totaal dus  10 + 5 • 3 = 25 partities van 3.

Een recursieformule.

Voor grotere getallen is zo'n slimme redenering veel meer werk en ook gevaarlijker, want je "vergeet maar zo eens wat".
Laten we proberen een recursieformule op te stellen.

de overgang van n naar n  + 1
Stel je stapt een kamer binnen met daarin n andere mensen, en jullie moeten worden verdeeld in k groepen.
Je kunt je op twee manieren opstellen.
• Stel je bent asociaal en vormt een groep helemaal in je eentje. Dan moeten die andere n mensen dus in k-1 groepen worden verdeeld, en dat kan op  Snk -1  manieren
• Stel je sluit je aan bij anderen. Dan zouden die anderen eerst k groepen kunnen maken, en vervolgens kun jij één van die k groepen kiezen om je bij aan te sluiten.
Dat kan dus op  Snk • k  manieren.
Samen moeten deze twee opties precies het aantal manieren opleveren om een groep van n + 1 in k partities te verdelen, dus:
       

Sn+1k = Snk-1 + k • Snk
       
Inde tabel hierbopven beschrijft deze regel hoe je in een kolom omlaag kunt gaan.
Bijvoorbeeld  S83  = 966 en die kun je vinden door  3 • 301 + 63 van de rij erboven te nemen (de 3 is k).
Zo is de hele tabel vrij makkelijk op te bouwen.
       
laten we huizen gaan verven.
Stel dat we k kleuren verf hebben waarmee we n huizen willen verven. Op hoeveel manieren kan dat dan?
Als er verder geen voorwaarden zijn kan dat natuurlijk op  kn manieren, want voor elk huis kun je uit k kleuren kiezen.
Maar als elke kleur gebruikt moet worden?

Dat is nou typisch een werkje voor het exclusie-inclusie principe!
Stel Ai is de eigenschap dat geen enkel huis kleur i krijgt.  Dan geldt:

n(A1∪A2∪A3∪...∪ Ak) =
  + nA1 + nA2 + nA3 + ...
   - nA12 - nA13 - ....
  + nA123 + nA124 + ...
   - nA1234 - nA1235 - ...
   ....
   +(-1)k-1 A123..k    
Die bovenste n(A1∪A2∪A3∪...∪Ak) is het aantal manieren dat één of meer kleuren niet gebruikt zijn.
Voor het aantal manieren waarbij alle kleuren gebruikt zijn moeten we dus nemen kn - n(A1∪A2∪A3∪ ... ∪Ak)
Laten we de berekening hierboven per regel bekijken:

nA1 = nA2 = nA3 = ....  = (k - 1)n  immers als één kleur niet gebruikt is, zijn er voor  n huizen (k - 1) kleuren beschikbaar.
hier staan  k  zulke termen.

nA12 = nA13 = ..... = (k - 2)n  immers als 2 kleuren niet gebruikt worden zijn er voor n huizen (k - 2) kleuren beschikbaar.
hier staan  (k nCr 2) zulke termen, immers je moet 2 kleuren uit de k kiezen om niet mee te verven)

enzovoort.

Dat geeft het volgende resultaat  (noem N0 = aantal manieren met alle kleuren gebruikt):
       

       
Maar je kunt het ook zó zien:  verdeel de huizen eerst in k verzamelingen.  Dat kan op  Snk manieren.
Verdeel daarna de k kleuren over die k verzamelingen. Dat kan op  k! manieren.
In totaal kun je n huizen dus op  Snk • k!  manieren met k  kleuren verf kleuren. 
En dat moet gelijk zijn aan N0 hierboven.
Slotformule:

       

© h.hofstede (h.hofstede@hogeland.nl)