© h.hofstede (h.hofstede@hogeland.nl)

Boek I, propositie 22.
       

Met drie lijnstukken (waarvan de som van twee steeds groter is dan de derde) kun je een driehoek construeren.
       
 

Neem drie lijnstukken l1, l2 en l3.

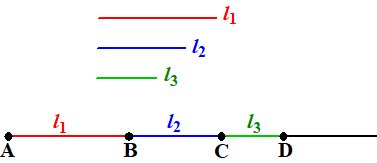Begin met een halve lijn vanaf punt A, en teken de punten B en C en D zodat AB = l1 en BC = l2  en  CD = l3.
   
 

 

 

Teken de cirkel met middelpunt B en straal  AB = l1
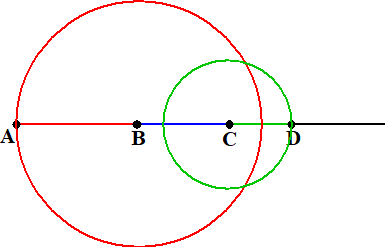Teken de cirkel met middelpunt C en straal  CD =l3
       
 

E is een snijpunt van de cirkels.
Teken EC en EB
Dan is EB = BA = l1  en   EC = CD = l3

Dus is BCE de gevraagde driehoek.
       
 
       
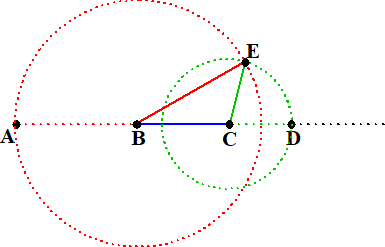Muggenzifterij:
Euclides stelt dat de voorwaarde dat twee van de drie lijnstukken steeds groter zijn dan de derde een noodzakelijke voorwaarde is. Hij laat nergens zien dat het ook een voldoende voorwaarde is. Hoe weet je dat de twee cirkels elkaar inderdaad snijden.......?
       

© h.hofstede (h.hofstede@hogeland.nl)