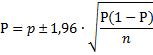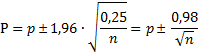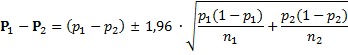proporties toetsen

© h.hofstede (h.hofstede@hogeland.nl)

De standaarddeviatie van een Proportie.

In principe is het meten van een proportie (percentage) natuurlijk niets anders dan het meten van een gemiddelde. Stel je maar een vaas voor vol met enen en nullen. Bijvoorbeeld 1 = voorstander en 0 = tegenstander.
De proportie voorstanders in je steekproef (p) is dan gewoon niets anders dan het gemiddelde van de waarde van de 0-1 knikkers die je hebt getrokken.

Hoe is het dan met de proportie (P) in de hele populatie?

Voor gemiddelden hadden we bij het 95%-betrouwbaarheidsinterval de formule
μ = [X - 1,96σ,   X + 1,96σ]

Een zelfde formule voor proporties zou dan geven:
P = [p - 1,96σ,   p + 1,96σ]     ..... (1)

Alleen nu is het probleem dat die σ afhangt van P!
We weten immers dat voor een binomiale verdeling geldt σ = √(^{P(1 - P)}/_n)
Dus dan staat die P daar links én rechts in vergelijking (1), want die ziet er dan zó uit:

Hoe lossen we dat op?

1. Voor erg grote n.

Zeg maar zo ongeveer n > 100

In dat geval doen we gewoon alsof de proportie in de steekproef gelijk is aan de populatieproportie (net zoals we bij de standaarddeviaties deden). Dus we stellen aan de rechterkant van de vergelijking: P ≈ p

2. Voor gemiddelde grote n.

Zeg maar zo ongeveer 50 < n < 100
Nu zijn er twee mogelijke opties

De eerste optie is is nogal ruw en grof. We nemen daarbij gewoon de t-waarde in plaats van de z-waarde, en vervangen net als in het geval van grote n de P door p.
Waarom is deze methode dan zo ruw en grof? Nou, de t-verdeling is ooit afgeleid uitgaande van een normaal-verdeelde populatie. En we hebben hier te maken met een populatie van alleen maar enen en nullen; dus absoluut niet normaal verdeeld!

De tweede optie is, om rekening te houden met het "ergste wat er zou kunnen gebeuren".
De maximum waarde van P(1 - P) is gelijk aan 0,25 (namelijk bij P = 0,5). Daarom stellen we:

Bedenk wel dat deze methode wat conservatief is: hij gaat uit van een soort "worst-case-scenario". Eigenlijk levert hij dus een betrouwbaarheidsinterval van minstens 95% in plaats van precies 95%. In gevallen waarbij P vermoedelijk in de buurt van 0,5 ligt (democraten tegen republikeinen in de VS), geeft de methode wel een goed betrouwbaarheidsinterval.

3. Voor kleine n

Zeg maar zo ongeveer n < 50.
Laten we eens kijken wat we nou eigenlijk al die tijd aan het doen zijn:

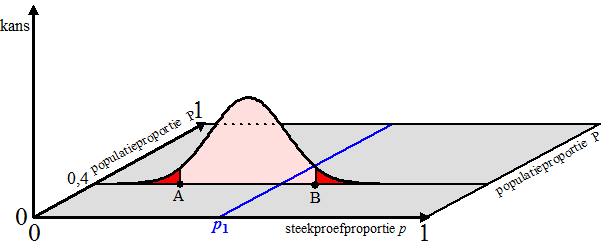
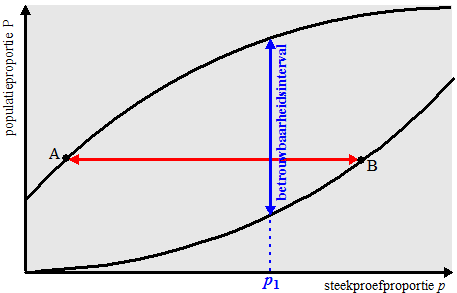
In het grijze vlak zie je de steekproefproportie p uitgezet tegen de (nog onbekende) populatieproportie P. Dit alles bij een gegeven n. Bij elke populatieproportie P hoort een kansverdeling van p, zoals hierboven is getekend voor P = 0,40.
De kans op een gemeten waarde p₁ moet nu binnen de 5%-grenzen A en B liggen, dus er is een 95% kans dat een
gemeten p in het interval AB komt te liggen.

Maar toen draaiden we ineens de zaak om. Dat geeft het volgende bovenaanzicht:

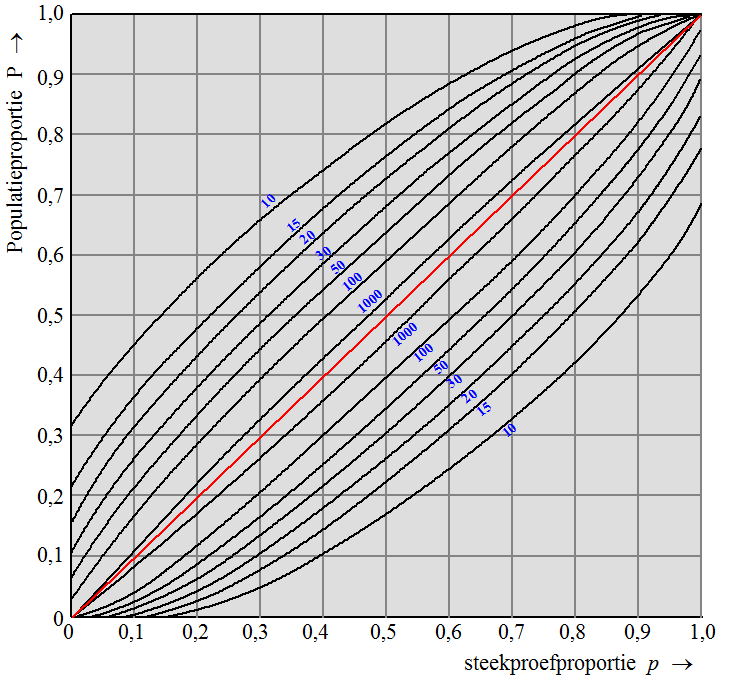
Voor elke P zijn er zulke A en B te vinden. Als je die allemaal tekent krijg je de twee kromme lijnen uit deze figuur (nog steeds voor één bepaalde n).
Maar dat betekent dat bij een gemeten p₁ alle P-waarden uit het blauwe interval een verdeling opleveren waarvoor p₁ binnen de 95%-grenzen valt: een betrouwbaarheidsinterval dus!!

In de volgende figuur zie je voor allerlei n-waarden die kromme lijnen waar A en B op liggen getekend.

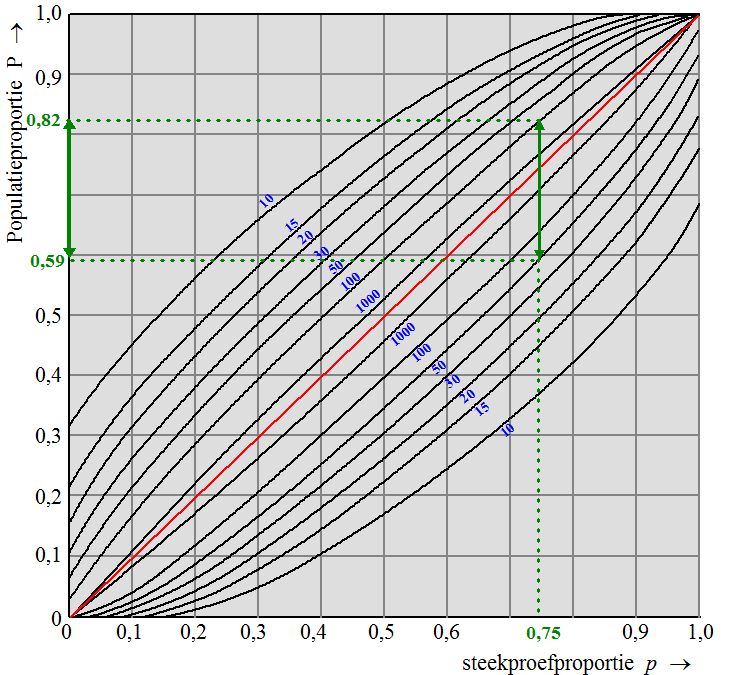
Hieronder zie je hoe het werkt.
Als je een steekproefproportie van p = 0,75 meet, en je steekproef had grootte n = 50, dan geeft dat een 95%-betrouwbaarheidsinterval [0.59, 0.82]

Een paar dingen die opvallen?
Als P nul is, dan moet ook p nul zijn (als dingen niet bestaan zullen ze ook niet in je steekproef voorkomen). Dat is de reden dat de onderste helft van de krommen (die ontstonden door de punten B) door de oorsprong gaan.
Maar de bovenste helft van de krommen gaat niet door de oorsprong. Dat betekent dat als je een waarde p = 0 in je steekproef aantreft, dat niet hoeft te betekenen dat P = 0 in de populatie (dingen die je niet in je steekproef aantreft kunnen nog best bestaan).

Verder valt het op dat de betrouwbaarheidsintervallen niet symmetrisch zijn. Behalve bij p = 0,5 is dat natuurlijk ook logisch. De binomiale verdeling is toch ook niet symmetrisch?

Het verschil van twee proporties.

Niet veel nieuws onder de zon hier..... Gaat hetzelfde als bij het verschil van twee gemiddeldes. Varianties optellen.

OPGAVEN

In een enquête onder 580 studenten in Nederland vond men dat 35% van hen vond dat Nederland uit de Europese Unie moest treden.

Geef een 95%- betrouwbaarheidsinterval voor het percentage van alle studenten in Nederland dat vindt dat Nederland uit de Europese Unie moet treden.

De groep van 580 bestond uit 290 ouder dan 24 jaar en 290 jonger dan 24 jaar.
In de eerste groep was 40% vóór uittreding, en in de tweede groep 30%.

Geef een 95%-betrouwbaarheidsinterval voor het verschil in percentages onder beiden groepen in de hele populatie.

Hoe verandert je antwoord op vraag b) als de groepen niet 290-290 waren, maar 400 (ouder dan 24) -180 (jonger dan 24)?

Bij kwaliteitscontrole in een geneesmiddelenfabriek blijkt in een steekproef van 150 exemplaren dat 12% niet voldoet aan de strenge kwaliteitseisen.

Welk 95%-betrouwbaarheidsinterval volgt hieruit voor het percentage exemplaren in de hele productie dat niet voldoet aan de eisen?

Hoe verandert het antwoord op vraag a) als de steekproef bestond uit 10 exemplaren?