| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
|
|
|
|
Priemgetallen met de GR. |
| |
|
|
|
Deze les gaan we een
programmaatje voor de GR maken dat een lijst van priemgetallen voor ons
produceert.
Zoals je weet is een priemgetal een getal dat precies 2 delers heeft,
namelijk 1 en zichzelf (het getal 1 is geen priemgetal!)
Om te testen of een getal een priemgetal is moet je dus gewoon proberen
het door alle getallen tussen 1 en zichzelf te delen.
Als dat nooit lukt heb je een priemgetal.
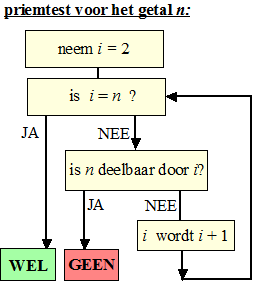
Programmeurs zien dan direct in hun hoofd een stroomdiagram om te
testen of een getal een priemgetal is: |
| |
|
|
|
|
 |
| |
|
|
|
Ga na dat dit werkt:
we proberen alle getallen van 2 tot n en zodra we een deler
vinden stoppen er mee. Als dat tot het eind niet lukt dan hebben we een
priemgetal gevonden.
Hoe test je of een getal n
deelbaar is door een getal i? |
| |
|
|
|
Daar is de integer
functie erg handig voor.
Immers, als n deelbaar is door i dan is
n/i een geheel getal. De
integer-functie kan testen of een getal geheel is, want als dat zo is
dan is INT(getal) = getal (immers bij een geheel getal
verandert er niets aan het getal als je INT ervan neemt) |
| |
|
|
|
|
n/i
is geheel als INT(n/i)
= n/i |
|
| |
|
|
|
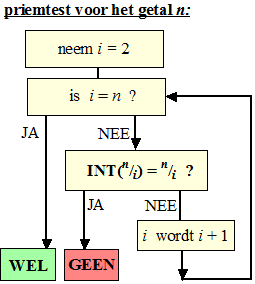
| daarmee wordt het
stroomdiagram zó: |
| |
|
|
|
|
 |
| |
|
|
|
|
Een behoorlijke versnelling... |
| |
|
|
|
Het is niet nodig om
alle getallen van 2 tot n te testen.
Dat zit hem in het feit dat delers altijd in koppeltjes voorkomen.
Kijk bijvoorbeeld naar de delers van 24:
24 = 2 • 12 = 3 • 8 = 4 • 6 = 6 • 4
= 8 • 3 = 12 • 2
Omdat 24 = √24 •
√24 is steeds één van beide
delers groter dan √24 en de ander
kleiner dan √24
Maar dat betekent dat je voor de delers alleen maar de getallen kleiner
dan √24 hoeft te testen! Als daar
geen deler bij is, is er ook geen deler groter dan
√24.
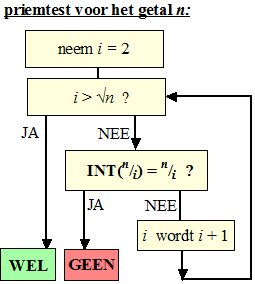
Dat betekent dat we kunnen stoppen met testen zodra i groter dan
√n is geworden.
Dat geeft het volgende stroomschema: |
| |
|
|
|
|
 |
| |
|
|
|
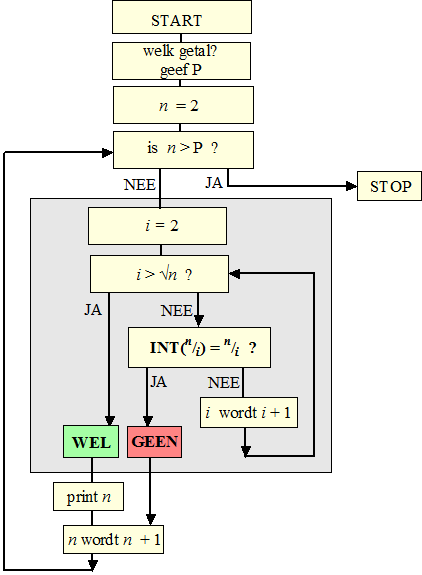
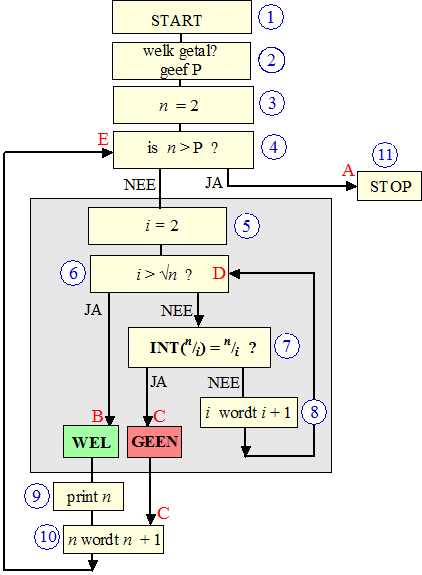
Een lijst met priemgetallen maken.
We gaan nu ons programmaatje uitbreiden zodat de gebruiker een getal kan
geven (we noemen het P), waarvoor het programma vervolgens alle priemgetallen kleiner dan
dat getal afdrukt.
Dat ziet er zó uit (in het grijze blok staat ons vorige
stroomschema): |
| |
|
|
|
|
 |
| |
|
|
|
Oké, en nu een echt programma graag!
Laten we dat stroomschema hierboven gaan vertalen naar een programma op
de GR.
Blokje voor blokje maar....... In onderstaande uitleg is Blauw de
menuknoppen van je TI, Rood is wat je op je scherm krijgt, de
rest is commentaar/toelichting.
"Lbl" betekent "Label" en is een manier om een plaats in het programma
een naam te geven (zodat je er later naar toe kunt gaan als dat nodig
is). |
| |
|
| 1. |
START.
Dat doe je met
PRGM NEW 1:Create New
Laten we het bij Name = maar
"PRIEMGETAL" noemen. |
 |
| |
|
|
| 2. |
PRGM I/O
staat voor
Input/Output en daarmee kun je getallen invoeren of laten uitvoeren.
PRGM I/O 1:
Input
"welk getal?", P
(Die komma is de dikke komma) |
| |
|
|
| 3. |
2 STO
N
geeft in je scherm:
2 →
N
Daar staat eigenlijk: "Sla het
getal 2 op in geheugen N" |
| |
|
|
| 4. |
Nu moeten we testen
of N groter dan P is. Als dat zo is, dan stoppen we, als dat niet
zo is dan gaan we door.
PRGM 9: Lbl E:
PRGM 1:
If (N 2nd TEST
> P) : PRGM 0: Goto A
(Als N nu groter is dan P dan springt het programma naar plaats A (die
we later zullen aangeven). Als dat niet zo is gaat het programma gewoon
verder naar 5. |
| |
|
|
| 5. |
2 STO I
(net zoals stap
3) 2
→
I |
| |
|
|
|
| 6. |
PRGM 9: Lbl D:
PRGM 1: If (I
2nd TEST >
√(N)) :
PRGM 0:
Goto B |
 |
| |
|
|
| 7. |
PRGM 1: If (MATH num
5: int(N/I)
2nd
TEST = (N/I)) :
PRGM 0: Goto C |
| |
|
|
| 8. |
I + 1
STO →
I : PRGM 0 : Goto D |
| |
|
|
| 9. |
PRGM 9:
Lbl B:
PRGM I/O 3: Disp N |
| |
|
|
| 10. |
PRGM 9: Lbl C:
N + 1
STO
→
N :
PRGM 0: Goto
E |
| |
|
|
| 11. |
PRGM 9: Lbl A:
PRGM F: Stop |
| |
|
|
|
| Daarmee ziet ons hele
programmaatje er zó uit: |
| |
|
|
|
|
 |
| |
|
|
|
| Nou is dit met al die
Lbl's en Goto's een erg lelijk programmaatje, maar daar gaat het nou
eventjes niet om. Het levert wel priemgetallen. Probeer dat zelf maar
uit door het programmaatje te laten lopen: PRGM
EXEC en kies dan PRIEMGETAL |
| |
|
|
|
| 1. |
Pas het programmaatje hierboven aan zodat het
niet alleen de priemgetallen geeft, maar ook zegt HOEVEEL het er
zijn. (tip: maak een teller T die je in het begin nul
stelt, en die elke keer als je een priemgetal hebt gevonden
eentje hoger wordt). |
| |
|
|
|
| 2. |
Maak een programma dat vraagt om een getal, en
dat vervolgens van dat getal alle delers geeft. |
| |
|
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|