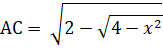|
|||||
| Pietje Precies. | |||||
| Het getal
π is intussen met snelle computers
berekend tot in talloze decimalen, maar je kunt je misschien voorstellen
wat een moeite de oude Grieken hadden om π te benaderen. Laten we
(voor de grap, echt nuttig is het niet) zelf ook eens gaan proberen wat
decimalen van π te vinden. En dan bedoel ik natuurlijk niet "even
Googelen". Bij een gegeven cirkel kun je een regelmatige driehoek vierhoek vijfhoek .... n-hoek tekenen die er precies in past. Dat ziet er ongeveer zó uit: |
|||||
|
|
|||||
| Hoe groter het aantal
hoeken wordt, des te meer gaat de veelhoek op de cirkel lijken. Dat
betekent dat de omtrek van de veelhoek nadert naar de omtrek van de
cirkel. Dus als we een manier vinden om de omtrek van een n-hoek
te berekenen, dan kunnen we de omtrek van een cirkel benaderen, en dan
kunnen we ook
π benaderen, want die omtrek is 2πr. Neem een cirkel met straal 1, dus met omtrek 2π. De ingeschreven driehoek heeft dan zijden van √3, dus omtrek 3√3. Dat geeft 2π ≈ 3√3 dus π ≈ 2,598... Het ingeschreven vierkant heeft zijden van √2 dus omtrek 4√2 Dat geeft 2π ≈ 4√2 dus π ≈ 2,828... De ingeschreven zeshoek heeft zijden van 1, dus omtrek 6 Dat geeft 2π ≈ 6 dus π ≈ 3 De ingeschreven twaalfhoek heeft zijden √(2 - √3) dus omtrek 12√(2 - √3) (uitleg hieronder!) Dat geeft 2π ≈ 12√(2 - √3) dus π ≈ 3,1058... Je ziet, dat nadert steeds dichter tot π. |
|||||
| Van n-hoek naar 2n-hoek. | |||||
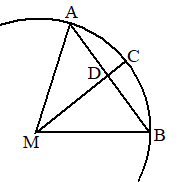
| Stel dat A en B twee
opeenvolgende hoekpunten zijn van een n-hoek waarvan alle
hoekpunten op de cirkel met straal 1 en middelpunt M liggen. Neem AB = x Teken de middelloodlijn MC van AB. In driehoek ADM geldt: (1/2x)2 + MD2 = 12 Dus MD = √(1 - 1/4x2) CD = MC - MD = 1 - √(1 - 1/4x2) In driehoek ADC geldt: AC2 = (1/2x)2 + (1 - √(1 - 1/4x2))2 |
|
||||
|
|
|||||
| Conclusie: | |||||
|
|||||
| En nu gaat het benaderen veel sneller. Begin bijvoorbeeld met een vierkant: | |||||
| • | Een vierkant heeft zijden √2, dus omtrek 4√2, dus π ≈ 2√2 = 2,828... | ||||
| • | Een achthoek heeft zijden √(2 - √2) dus omtrek 8√(2 - √2) dus π ≈ 4√(2 - √2) = 3,061.... | ||||
| • | Een zestienhoek heeft zijden √(2 - √(2 + √2)) dus π ≈ 8√(2 - √(2 + √2)) = 3,121... | ||||
| • | Een 32-hoek heeft zijden √(2 - √(2 + √(2 + √2))) dus π ≈ √(2 - √(2 + √(2 + √2))) = 3,136... | ||||
|
• |
Een 4096-hoek geeft π ≈ √(2 - √(2 + √(2 + √2 + ..... en dat geeft al ongeveer 3,141594.... | ||||
| Recursief. | |||||
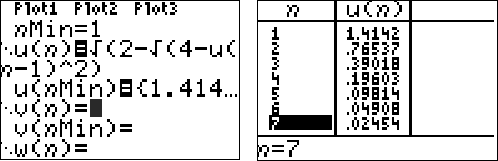
| Je herkent natuurlijk
direct uit het vorige voorbeeld de recursierelatie
un = √(2 - √(4 - un-12
)). In voeren in de GR dus maar, en in de tabel vindt je de achtereenvolgende waarden van de zijden, te beginnen bij u1 = √2 |
|||||
|
|
|||||
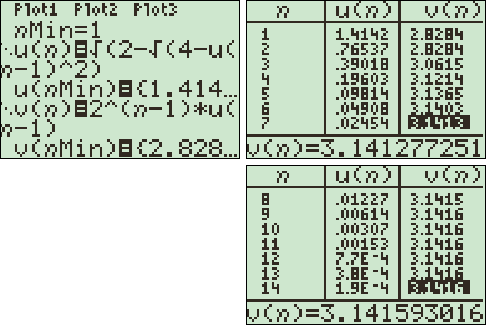
| Wacht, dat kan
mooier... De omtrek is steeds 2n + 1 keer de lengte van een zijde, en π is daarna de helft daarvan, dus 2n keer de zijdelengte. Dus kunnen we ook in één keer een rijtje benaderingen voor π in beeld krijgen in v(n): |
|||||
|
|
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||