permutaties met stijgingen

© h.hofstede (h.hofstede@hogeland.nl)

Permutaties met stijgingen.

We weten al hoe we het aantal permutaties van een serie moeten berekenen.
De getallen 1 tm 4 kun je bijvoorbeeld op 4! = 24 manieren rangschikken.
Deze les gaan we kijken naar het aantal stijgingen in zo'n serie. Als je bijvoorbeeld de volgorde 2134 hebt, dan heeft die twee stijgingen, namelijk van 1 naar 3 en van 3 naar 4.
Alle 24 gevallen mogelijkheden:

permutatie	aantal stijgingen
1234	3
1243	2
1324	2
1342	2
1423	2
1432	1
2134	2
2143	1
2314	2
2341	2
2413	2
2431	1
3124	2
3142	1
3214	1
3241	1
3412	2
3421	1
4123	2
4132	1
4213	1
4231	1
4312	1
4321	0

Samengevat:

Aantal stijgingen	0	1	2	3
Frequentie	1	11	11	1

De vraag is nu: kunnen we die onderste rij 1-11-11-1 ook voor andere waarden (ipv 4) berekenen?
Ik ben maar eens op onderzoek uitgegaan (nou ja, onderzoek... gewoon een boel saai uitschrijven), en dat leverde de volgende waarden op:

n	stijgingen
	0	1	2	3	4	5	6
1	1
2	1	1
3	1	4	1
4	1	11	11	1
5	1	26	66	26	1
6	1	57	302	302	57	1
7	1	120	1191	2416	1191	120	1

Laten we proberen om een recursieformule af te leiden.
Stel dat ik wil weten hoeveel manieren er zijn om 3 stijgingen in de getallen 1 tm 6 te hebben. Laten we dat aantal A(6, 3) noemen.
Elke volgorde van de getallen 1 tm 6 kan ik krijgen door het getal 6 toe te voegen aan een volgorde van de getallen 1 tm 5.

Laten we eens zo'n volgorde nemen, bijvoorbeeld 1 3 4 2 5 met 3 stijgingen
Er zijn nu 6 plekken waar ik het getal 6 kan toevoegen: 6-1-6-3-6-4-6-2-6-5-6
Laten we eens kijken wat er gebeurt met het aantal stijgingen. Er zijn vier mogelijkheden voor de plek waar 6 geplaatst wordt:

•

Als je 6 helemaal aan het begin zet (613425) dan levert dat geen extra stijging op.

•

Als je 6 helemaal aan het eind zet, dan levert dat één extra stijging op (134256).

•

Als je 6 in een stijging zet (163425) , dan komt er een stijging bij en er gaat eentje vanaf, dus het aantal stijgingen blijft gelijk.

•

Als je 6 in een daling zet (134625), dan komt er een stijging bij, en er gaat geen een vanaf, dus dat levert één extra stijging op.

Dat geeft de volgende recepten om een serie van 6 getallen met 3 stijgingen te krijgen

neem een serie van 5 getallen met 3 stijgingen en zet de 6 aan het begin of in een stijging.

neem een serie van 5 getallen met 2 stijgingen en zet de 6 aan het eind of in een daling.

Bij optie 1 heb je 4 mogelijke plaatsen voor de 6 (eind plus 3 stijgingen)
Bij optie 2 heb je 3 mogelijke plaatsen voor de 6 (begin plus 2 dalingen)
Dus A(6,3) = A(5,3) • 4 + A(5, 2) • 3

Controleren met de tabel: A(6, 3) = 26 • 4 + 66 • 3 = 302. KLOPT!!!!

Nu met variabelen....

Noem a het aantal cijfers, en s het aantal stijgingen, dan hebben we hierboven dus A(6, 3) berekend. Laten we de getallen uit de laatste regel (A(6, 3) = 26 • 4 + 66 • 3 ) omzetten naar variabelen:

is A(a - 1, s)

is (s + 1) (s stijgingen plus aan het eind)

is A(a - 1, s - 1)

als je a - 1 getallen hebt, dan zijn er a - 2 tussenruimtes.
met s - 1 stijgingen is er dan nog plaats voor (a - 2) - (s - 1) dalingen, dus a - s - 1 dalingen.
maar je kunt ook aan het begin toevoegen, dus er zijn (a - s) mogelijkheden.

Dat geeft de volgende recursieformule:

A(a, s) = A(a - 1, s) • (s + 1) + A(a - 1, s - 1) • (a - s)

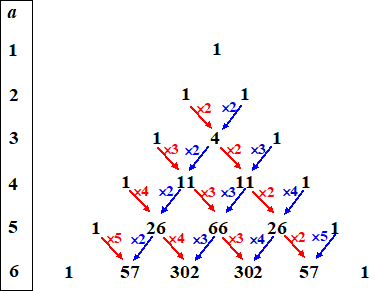
Hoe zo'n getal afhangt is mooi weer te geven door een soort "driehoek van Pascal" (maar dan anders):

Trouwens er zijn wel overeenkomsten tussen deze driehoek en die van Pascal.
• Als je de som van een rij bekijkt is dat steeds a!
• Als je een rij als histogram zou tekenen dan nadert dat voor grote a naar de normale verdeling.