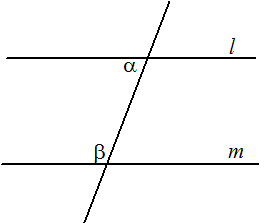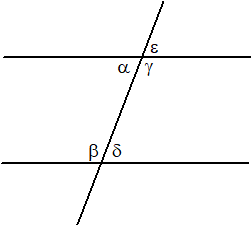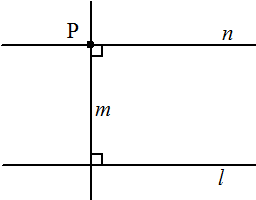© h.hofstede (h.hofstede@hogeland.nl)

Het parallellenpostulaat.
 

       
Hier zie je een van de oudste bewaard gebleven fragmenten van "De Elementen" ven Euclides. Euclides was een Griekse wiskundige die zo rond 300 voor Christus werkzaam was in de bibliotheek van Alexandrië,  en "De Elementen" was verreweg zijn belangrijkste werk.
"De Elementen" is een serie van  13 boeken waarin systematisch de hele meetkunde wordt  opgebouwd  uit een begin van 23 definities, 5 algemene inzichten en 5 postulaten.
Die 5 postulaten zijn de volgenden:
       
P1 Je kunt tussen twee punten een rechte lijn tekenen
   
P2 Je kunt een eindig lijnstuk verlengen tot een oneindig lange lijn.
   
P3 Je kunt een cirkel met een bepaald middelpunt en een bepaalde straal tekenen.
   
P4 Alle rechte hoeken zijn gelijk aan elkaar.
   
P5 Als een rechte lijn twee andere rechte lijnen snijdt, en de binnenhoeken aan dezelfde kant zijn samen minder dan twee rechte hoeken, dan zullen die twee lijnen, als je ze doortrekt, elkaar snijden aan die kant.
       
De hele meetkunde die uit deze vijf postulaten wordt opgebouwd noemen we dan ook de  "Euclidische Meetkunde".
 
Dat vijfde postulaat valt meteen op, omdat het veel ingewikkelder is geformuleerd dan de andere vier. Er hoort het plaatje hiernaast bij, en het zegt eigenlijk 

"Als a + b < 180º dan snijden l en m elkaar aan de kant van a en b"

Ook Euclides zelf zag dat dit postulaat apart was. Dit blijkt bijvoorbeeld al wel uit het feit dat hij dit postulaat pas gebruikte in Propositie I.29, en niet eerder.

Dit is trouwens die Propositie I.29:

       
Een rechte, die parallelle rechten treft, maakt de verwisselende binnenhoeken aan elkaar gelijk en den buitenhoek gelijk aan den afgelegen binnenhoek en de binnenhoeken aan den zelfden kant gelijk aan twee rechte [hoeken].
       
Daar staan eigenlijk 3 beweringen (zie de figuur hiernaast).
bewering 1:  α = δ   (wat wij  "Z-hoeken" noemen).
bewering 2:  ε = δ   (wat wij  "F-hoeken" noemen)
bewering 3:  γ + δ = 180º  ("twee rechte hoeken").   

Het bewijs  (uit het ongerijmde):
Stel dat α niet gelijk is aan δ, maar dat bijv. α > δ  (andersom gaat het bewijs precies hetzelfde)
Tel bij beiden γ op, dat geeft  α + γ > δ + γ
Maar α + γ = 180º dus δ + γ < 180º
Dan zouden de lijnen elkaar snijden (vijfde postulaat) en dat is niet zo.
Dus moet wel gelden  α = δ  (bewering 1).

       
α = δ  en ook  α = ε  dus  ε = δ  (bewering 2)
tel bij beiden γ op, dat geeft  ε + γ = δ + γ
Omdat ε + γ = 180º is dus δ + γ  = 180º  (bewering 3)
q.e.d.
       
Gelijkwaardige beweringen.
       
Er zijn een aantal alternatieve postulaten mogelijk die geheel gelijkwaardig zijn aan het vijfde postulaat van Euclides.
Hier volgen er een paar.

1.  Hoekensom driehoek.
2.  Playfair's Axioma.
3.  Axioma van Proclus.
4.  Stelling van Pythagoras.
5.  Stelling van de Buitenhoek.
6.  Drie punten liggen óf op een lijn óf op een cirkel.

Hier zijn wat bewijzen van hoe de één uit de ander volgt:
       
Vijfde postulaat ⇒  Hoekensom.  (propositie 32)
     
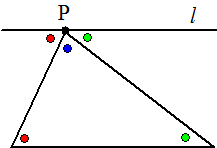
  Neem een driehoek en teken door punt P daarvan een lijn evenwijdig aan de tegenoverliggende zijde.

Dan volgt uit propositie I.29 hierboven dat de rode en groene hoeken gelijk zijn.
Maar de drie hoeken van de driehoek zijn dan gelijk aan de drie hoeken bij punt P, en die zijn samen een rechte lijn.
Conclusie:  Uit de postulaten van Euclides volgt dus dat de som van de hoeken van een driehoek 180º is (daar is wel het vijfde postulaat voor nodig).

       
  Geldt het ook andersom?
Jazeker: 
       
Hoekensom ⇒  Vijfde postulaat.
       
Vijfde postulaat ⇒  Playfair's axioma.
       
In 1795 gaf John Playfair, een Schots wiskundige, een alternatieve versie van het vijfde postulaat van Euclides, en die luidde als volgt:

(opmerking:  John zegt hier "hoogstens één lijn", maar omdat uit de andere vier postulaten is af te leiden dat er altijd minstens één zo'n lijn is, had hij net zo goed kunnen zeggen "precies één lijn".)

Het bewijs dat dit axioma volgt uit het vijfde postulaat van Euclides:
     
     

       
Playfair's axioma ⇒  vijfde postulaat
     
  Daarvoor leiden we eerst  de volgende stelling af: 
"Twee driehoeken in een driehoek zijn samen altijd minder dan 180º"
Dat is propositie I-17 van Euclides, dus daarvoor heeft hij zijn vijfde postulaat niet gebruikt.
Het bewijs van Euclides gaat zó:
       
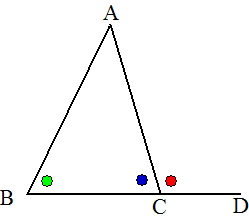
  Verleng in driehoek ABC zijde BC naar BD.
Zie de figuur hiernaast.

∠ACD (rood) is een buitenhoek van de driehoek is is daarom groter dan ∠ABC (groen)   (dat is propositie I-16).
Tel nu bij beiden blauw op, dat geeft
blauw + rood  > blauw + groen
Maar blauw  + rood = 180º,
Dus blauw + groen < 180º

Op dezelfde manier is dit voor elk ander paar van twee hoeken uit de driehoek te bewijzen.

       
  Daarna moet je bewijzen dat daaruit volgt dat drie hoeken van een driehoek altijd hoogstens 180º zijn, en dat doet de stelling van Sacchieri-Legendre.
 
       
       
3.  Axioma van Proclus.
       
4.  Oppervlakte van een driehoek.
       
5.  Eigenschap van 3 punten.
       
Vijfde postulaat  ⇒ Pythagoras.

Dat is propositie I-49 uit de Elementen en daar is het vijfde postulaat gebruikt.
       
Niet-Euclidische meetkunde

Lange tijd is er gedacht dat het vijfde postulaat af te leiden zou zijn uit de andere vier, maar dat blijkt niet het geval.
Dan rijst er natuurlijk meteen de vraag:  Wat gebeurt er als we het vijfde postulaat weglaten? Of vervangen door een ander postulaat?
Dan krijgen we dus meteen een heel ander soort meetkunde.
Een meetkunde waar de som van de hoeken van een driehoek niet meer 180º hoeft te zijn......
Een meetkunde waar de stelling van Pythagoras niet meer geldt.....

Hoe zou dat er uit zien?
Lees daarvoor de volgende lessen.

Ik ben nu al benieuwd!!!!!!
       
       

© h.hofstede (h.hofstede@hogeland.nl)