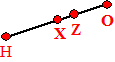negenpuntscirkel

© h.hofstede (h.hofstede@hogeland.nl)

De negenpuntscirkel.

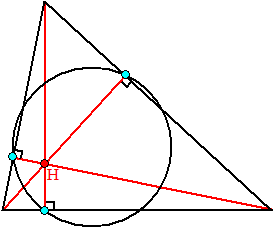
Deze les gaan we een beroemde en erg mooie cirkel die bij een driehoek hoort bekijken.
Het begint met de drie hoogtelijnen en hun snijpunt H.

De drie voetpunten waar die hoogtelijnen de zijden van de driehoek snijden liggen op een cirkel
(ja dûh, drie punten liggen bijna altijd wel op een cirkel!):

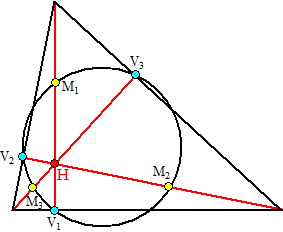
Deze cirkel heet ook wel de cirkel van Feuerbach of de negenpuntscirkel.

Negen? Waarom negen?

Dat komt hierdoor:
Bekijk nu eerst de snijpunten van die hoogtelijnen met deze cirkel:

Die drie punten zijn precies de middens van de lijnstukken die van het hoogtepunt naar de hoekpunten lopen!!

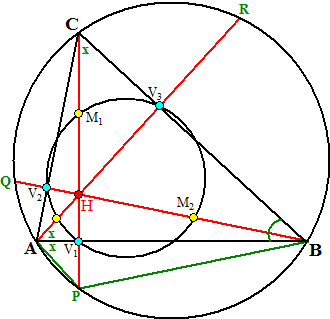
Waarom dat zo is kun je hiernaast zien.

De driehoeken CV₁B en AV₃B hebben beiden een rechte hoek en hoek B, dus zijn gelijkvormig. Dus zijn de hoeken met het groene kruisje ook gelijk.

Verleng nu de hoogtelijn uit C totdat hij de omgeschreven cirkel van de driehoek snijdt in P.
Dan is die andere hoek bij A ook een groen kruisje waard (beiden de omtrekshoek van boog PB).

Omdat ook AV₁ loodrecht op HP staat is HV₁ = PV₁ (AHV₁ en APV₁ zijn congruent: HHZ)
Conclusie: V₁ is het midden van HP.

Op precies dezelfde manier kun je aantonen dat V₃ en V₂ de middens van HR en HQ zijn.

Dat betekent dat de omgeschreven cirkel van de driehoek bij vermenigvuldiging met centrum H en factor ¹/₂ overgaat in de negenpuntscirkel.
Maar dan gaan A, B, en C over in M₃, M₂ en M₁ dus dat zijn inderdaad de middens!

We hebben nu dus al een zespuntscirkel.
Laten we die drie andere snijpunten van deze cirkel met de driehoekszijden bekijken. Zou daar ook iets leuks mee aan de hand zijn? Ik denk het wel.......Kijk maar mee:

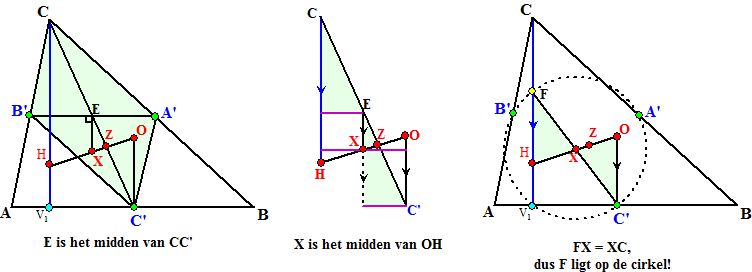
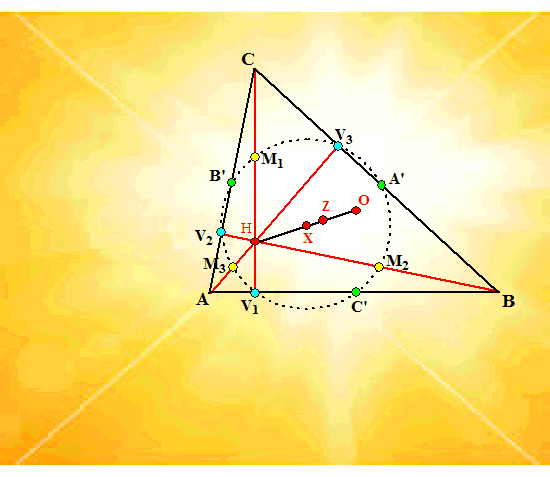
In de linkerfiguur gaan we op zoek naar de cirkel waar de middens A', B' en C' op liggen. Om precies te zijn: we gaan het middelpunt X van die cirkel zoeken.
Dat middelpunt is natuurlijk weer het snijpunt van de middelloodlijnen van A'B'C', en in de linkerfiguur is de middelloodlijn vanuit het midden E getekend.
Omdat A'C' en B'C' middenparallellen zijn is de groene figuur een parallellogram. Daarvan snijden de diagonalen elkaar doormidden, dus E is het midden van CC' . Tot zover de linkerfiguur....

In de middelste figuur zijn een aantal lijnen uit de vorige tekening gelicht. CH en EX en OC' zijn allemaal evenwijdig (want ze staan allemaal loodrecht op AB. Omdat CE = C'E zijn de twee groene driehoeken in deze figuur congruent (ZHH).
Maar dan zijn al die paarse lijnstukjes even lang.
Daarom is het snijpunt X van de middelloodlijn vanuit E met lijn OH het midden van OH.
Maar dit verhaal voor de middelloodlijn vanuit E geldt precies zo voor beide andere middelloodlijnen van A'B'C'.
Conclusie: Het middelpunt X van de cirkel door A'B'en C' is het midden van OH. Tot zover de middelste figuur....

In de rechterfiguur is C'X doorgetrokken totdat hij CH snijdt in punt F. Aan de groene zandloperfiguur is dan te zien dat FX = C'X (immers HX = OX) dus ligt F ook op de cirkel.
FC' is dus een middellijn van de cirkel.
Maar omdat FV₁C' een rechte hoek is, ligt dan punt V₁ óók op die cirkel (Thales strikes again!)
We zijn er: de cirkel door A'B'C' gaat ook door V₁, dus het moet wel dezelfde cirkel zijn als die eerdere cirkel door de voetpunten. (Je ziet trouwens meteen dat dat punt F natuurlijk eigenlijk het eerdere M₁ is)

Daarmee is onze cirkel met recht een negenpuntscirkel geworden. Hier zie je hem nog eens in zijn volle glorie, geniet er gerust een poosje van:

De rechte van Euler.

Ik wil toch nog even je aandacht vestigen op die mooie rechte lijn daar midden in die driehoek. Het is rechte van Euler, en daarop liggen vier interessante punten:

H: het snijpunt van de hoogtelijnen.
X: het middelpunt van de negenpuntscirkel.
Z: het snijpunt van de zwaartelijnen.
O: het middelpunt van de omgeschreven cirkel.

Verder liggen ze ook nog eens zó, dat X het midden van HO is, en dat Z op tweederde deel van HO ligt (dat zagen we al in een eerdere les).

Het kan niet op! Nóg een leuke eigenschap!

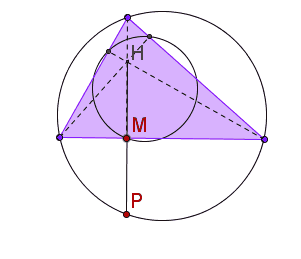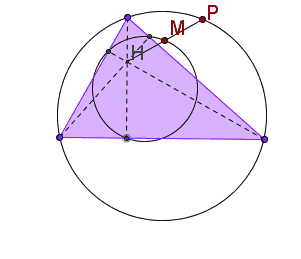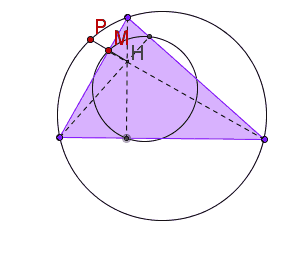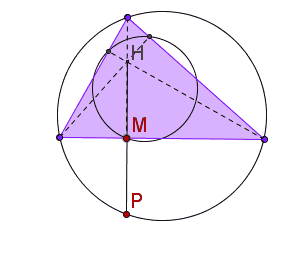
We vonden al eerder dat de omgeschreven cirkel bij vermenigvuldiging met centrum H en factor ¹/₂ overgaat in de negenpuntscirkel.
Kies een willekeurig punt P van de omgeschreven cirkel, dan ligt het midden M van HP dus op de negenpuntscirkel. Ofwel: Als P de omtrekscirkel doorloopt, dan doorloopt het midden M van HP de negenpuntscirkel.
De negenpuntscirkel is dus de conflictlijn van de omtrekscirkel en het hoogtepunt H.

Hiernaast zie je een Geogebra-animatie waarin dat allemaal aardig lijkt te kloppen.

Gelukkig maar.....

Voor nog wat stellingen over deze geweldige cirkel moet je deze les over de "stelling van Feuerbach" maar lezen.