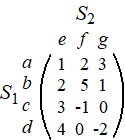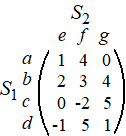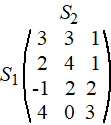|
|||||
| Evenwicht. | |||||
| Neem de volgende matrix van een tweepersoons-nulsomspel. | |||||
|
|
|||||
| S1
heeft de keuze uit de strategieŽn a, b, c, d en S2
heeft de keuze uit e, f, g. Dan zou de volgende discussie kunnen ontstaan: S1: "Ik kies b" S2: "Oh, dan kies ik c want dat geeft jou de kleinste winst ". S1: "Ja maar als jij c kiest, dan kies ik a, want dan heb ik meer winst" S2: "Ja maar als jij a kiest dan kiest ik e S1: "Oh nou, dan kies ik d" S2: "Nou dan kies ik g" S1: "Nou dan kies ik a" ..... en zo gaat dat alsmaar door. Ze gaan het niet eens worden want elke keer is er voor iemand wel een reden om een nieuwe betere strategie te kiezen. Maar stel nou dat bij een ander spel deze matrix geldt: |
|||||
|
|
|||||
| Daar gaan we weer: S1: "Ik kies a" S2: "Dan kies ik g" S1: "Dan kies ik c" S2: "Dan kies ik f " S1: "Dan kies ik d" S2: "Dan kies ik e" S1: "Dan kies ik b" S2: "Dan kies ik ........ En nu blijft het stil!!!! S2 blijft bij zijn keuze en S1 ook. |
|||||
| Bij de keuze van
strategieŽn b en e is er voor niemand meer reden om van
keuze te veranderen. Kennelijk is er een soort evenwicht bereikt. Zo'n evenwicht noemen we een Nash-evenwicht. naar de Amerikaanse wiskundige John Nash. (1928-2015). Hij heeft er zelfs (met 2 anderen samen) de Nobelprijs voor de economie voor gekregen. Trouwens niet alleen voor bovenstaand evenwicht, want waarschijnlijk denk je nu "Dat had iik ook nog kunnen verzinnen". Nash toonde aan dat zulke evenwichten ook bij ander soort spellen bestaan. Daar gaan de volgende twee lessen over. Hij was een geniaal wiskundige maar leed een groot deel va zijn leven aan paranoÔde schizofrenie. Dat maakte hem hoofdpersoon in de film "A Beautiful Mind" (Nash wordt daarin gespeeld door Russell Crowe) |
a |
||||
|
Nash-Evenwicht. Wanneer treedt er nou een Nash-evenwicht op, en wanneer niet? Stel dat er zo'n evenwicht bij rij i en kolom j optreedt, dus bij het element aij Het feit dat beide spelers geen reden hebben om van strategie te wisselen betekent eigenlijk: - het element aij is de grootste in de rij i - het element aij is het kleinste in kolom j Zo'n element dat tegelijkertijd de grootste in zijn rij en de kleinste in zijn kolom is noemen we een zadelpunt. Wiskundig geformuleerd: |
|||||
|
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||