© h.hofstede (h.hofstede@hogeland.nl)

Delen met modulo.
       
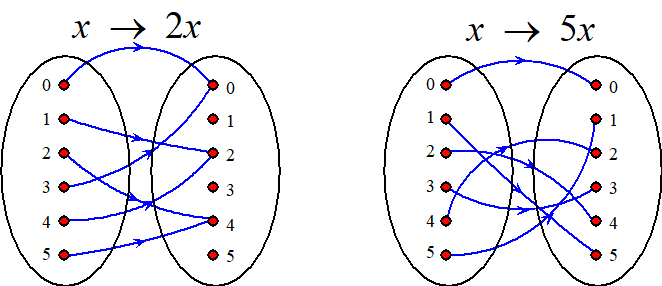
De vorige les zagen we, dat je veel van wat met  gewone vergelijkingen mag, ook met modulorekenen mag.  Je mocht bijvoorbeeld optellen, vermenigvuldigen en machtsverheffen.
Hoe zit het met delen?

Dat geeft soms wat verrassende problemen. Laten we twee afbeeldingen bekijken,  namelijk die van  x → 2x en die van x → 5x,  beiden op de verzameling {0, 1, 2, 3, 4, 5}:  de restklassen modulo 6.
Die vermenigvuldigingen zien er zó uit:
       

       
Zie je het verschil?
Als je delen zou willen omschrijven als het omgekeerde van vermenigvuldigen, dan zou je in deze twee figuren de pijlen dus moeten omdraaien.  Maar in de linkerfiguur geeft dat problemen, omdat er bijvoorbeeld TWEE pijlen van uit de getallen vertrekken. Dan zou bijvoorbeeld 4/2 gelijk kunnen zijn aan 2 maar ook aan 5!!!  "Delen" is dan geen éénduidige bewerking.
Bovendien zouden de getallen 1, 3 en 5 dan niet door 2 gedeeld kunnen worden!
Dat probleem ontstaat omdat 2 van 2x een deler is van 6.

In de rechterfiguur heb je dat probleem niet; dan gaat er bij omdraaien gewoon weer 'één pijl vanuit elk getal naar de overkant.  5 van 5x is géén deler van 6.
       
Laten we beginnen met het begrip  inverse:
       

x is een inverse van a (mod b)  als geldt:      ax ☰ 1 (mod b)
       
We noteren dat als x = a-1 .
Let nog even op het woordje "een". Dat staat er niet voor niets  (zagen we bovenaan al bij x → 2x).
Zo is 5 bijvoorbeeld een inverse van 8 (mod 13)  want  5 • 8  (mod 13) ☰ 1.
Maar ook 18 is een inverse, want ook 18 • 8 (mod 13) ☰ 1. En zo zijn er nog oneindig veel meer inversen.

Je kunt de definitie ook nog een klein beetje veranderen:
ax ☰ 1 (mod b)  betekent  dat  ax = 1 - yb  ofwel    ax + by = 1
Het bestaan van een inverse is dus hetzelfde als het bestaan van een oplossing van de Diophantische vergelijking ax + by = 1,

En daaruit volgt dan weer dat a een inverse mod b heeft als  ggd(a, b) = 1. En al die inversen zijn hetzelfde (mod b).
Dus om een inverse te vinden kunnen we ook gewoon de Diophantische vergelijking ax + by = 1 oplossen. Dat hebben we in een eerdere les al gedaan.
       

x is een inverse van a (mod b)  ⇔  ax + by = 1
       
Lineaire congruenties.
       
Stelling:      

Als ggd(x, y) = 1  dan geldt:
   x ☰ y (mod m)  ⇔  dx ☰ dy  (mod m) 

       
Hier staat eigenlijk dat je beide kanten mag delen als er een inverse bestaat.
Dat bestaan van die inverse is wel nodig. 
Zo is bijvoorbeeld 2 • 3 ☰ 2 • 5  (mod 4) maar niet  3 ≠ 5 (mod 4).  Dat komt omdat  2 geen inverse heeft (mod 4).

Eigenlijk doen we hetzelfde als bij gewone vergelijkingen.
Als je de vergelijking  5x = 12 wilt vereenvoudigen dan vermenigvuldig je eigenlijk beide kanten met de inverse cvan 5, namelijk met 1/5, dus dat geeft  1/5 • 5x = 1/5 • 12.  Het enige verschil bij modulorekenen is dat die inverse nu afhangt van de modulus.
Dus  5x = 12  ⇔  5-1 • 5x = 5-1 • 12

Daarom noteren we vanaf nu de inverse a-1  (mod m)  als ggd(a, m) = 1  ook wel als  1/a .  En vooruit, als we toch bezig zijn, laten we dan ook maar meteen b/a  noteren als b • a-1 . Alles uiteraard alleen maar als  ggd(a, m) = 1.
En hopla, nog maar eentje:   (a-1)n  noteren we lekker als a-n . Dat voelt allemaal goed

Het komt er eigenlijk op neer dat, als ggd(a, m) = 1 gewoon "alles mag". 
Bijvoorbeeld dit rijtje:
       

Als ggd(a, m) = 1 dan geldt:  (alles mod m)
(a-1)-1 ☰ a
(ab)-1 ☰ a-1b-1
1/(1/a) ☰ a
a-n ☰ (an)-1
ax • ay ☰ ax + y 

       
De volgende stelling gaat over het oplossen van vergelijkingen (mod m):
       

ax ☰ b (mod m)  heeft oplossingen  ⇔  ggd(a, m) | b

in dat geval zijn er precies ggd(a, c) oplossingen (mod m)
       
Bewijs:
  ax ☰ b (mod m) oplossen is hetzelfde als het vinden van oplossingen van  ax + my = b, en daarvan zagen we de les over Diophantische vergelijkingen al dat er alleen oplossingen zijn als ggd( a, m) | b
Als je een oplossing x0 hebt, dan wordt de algemene oplossing gegeven door  x0 + km/d  met   d = ggd(a, m)
We willen natuurlijk alleen de oplossingen in het interval  [0, m - 1]
k = 1, 2, 3, ..., d  geeft precies die oplossingen, dus dat zijn er d
q.e.d.  
       
Voorbeeld.
Los op:  6a ☰ 75  (mod 21)
ggd(6, 12) = 3 en dat is een deler van 75, dus er zijn oplossingen
één oplossing is bijvoorbeeld  a = 2   (want 12 (mod 21) ☰ 75 (mod 21) ☰ 12)
Dat geeft in het interval  [0, 74]  de oplossingen   2, 27en  52

Welke getallen zijn eigenlijk hun eigen inverse (mod m)?

Dan moet gelden a2 + km  = 1
neem bijvoorbeeld m = 4  dan is de vraag:  welke kwadraten liggen op afstand 1 van de tafel van 4?
Bijvoorbeeld a = 3 en k = -2 geeft  9 - 8 = 1
of  a = 5  en  k = -6 geeft  25 - 24 = 1
of   

       
De Chinese Reststelling.
       
Net zoals er stelsels vergelijkingen zijn, zijn er ook stelsels van modulo-congruenties.  De Chinese Reststelling geeft aan hoe je oplossingen van zo'n stelsel kunt opsporen. Hier is íe:
       

Als m1, m2, ..., mn  coprieme gehele getallen zijn,
en a1, a2, ..., an zijn willekeurige gehele getallen,
dan bestaan er oneindig veel getallen x,  zodat x ☰ ai (mod mi) voor elke i.

       
Neem bijvoorbeeld de drie coprieme  m-waarden  4, 5 en 9  en de a-waarden  5, 3 en 4
Dan zoeken we een getal; zodat  x ☰ 5 mod(4)  en  x ☰ 3 mod (5) en x ☰ 4 mod (9)
Je ziet dat x = 13 aan alle drie voldoet.
En overigens ook 193, 373, 553 , 733, ......  :  dat is 13 mod(4 • 5 • 9) ☰ 13 mod (180).  
Dat laatste is trouwens altijd zo;  alle oplossingen voor x zijn mod (m1m2...mn).

Het lijkt logisch dat er zo'n oplossing bestaat.
Neem bijvoorbeeld het stelsel  x ☰ 7 (mod 4) en  x ☰ 12 (mod 5)
Alle getallen 7 (mod 4) zijn  7, 11, 15, 19, 23, 27, 31....
Alle getallen 12 (mod 5) zijn  12, 17, 22, 27, 32....
De eerste rij neemt stapjes van 4, de tweede stapjes van 5. Dus logisch dat ze ergens hetzelfde getal opleveren.
In dit geval is dat als eerste dubbele in de rijen x = 27  (en andere oplossingen zijn 47, 67, 87, ...)

Maar hoe noteren we zo'n bewijs wat wiskundiger?  
Nou, bijvoorbeeld zó:
       
Bewijs:
  hulpstellinkje:   als  ggd(a, b) = 1  en   x ☰ y (mod a) en ook  x ☰ y (mod b) dan is  x ☰ y (mod ab)
  a is een deler van  (x - y) en b is ook een deler van (x - y)
omdat ggd(a, b) = 1 moet wel gelden dat ab een deler is van (x - y) dus  x ☰ y  (mod ab)
q.e.d.  
Stel nu  x ☰  a1 (mod m1)  en  x ☰ a2 (mod m2)
De eerste kun je schrijven als  x = a1 + y • m1 
Vul die in in de tweede vergelijking:   a1 + y • m1  ☰ a2 (mod m2)

Omdat ggd(m1, m2) = 1  bestaat de inverse van m1 (mod m2) en die is éénduidig bepaald (zie bovenaan deze les).
Noem die inverse z,  dan geldt  y ☰ z • (a2 - a1)  (mod m2)  en die y is ook éénduidig bepaald.
Nu kun je x bepalen :    x ☰ a1 + z • (a2 - a1) • m1   (mod m1m2)
en die x is ook éénduidig bepaald (dat zegt het hulpstellinkje hierboven).

Met meer dan twee vergelijkingen gaat het precies zo. Je zou er eerst twee kunnen oplossen, en dan met die oplossing de derde erbij nemen en opnieuw oplossen, en dan de vierde, enz.
q.e.d.  
       
Dat vind is nou mooi:  een bewijs dat niet alleen laat zien dát er een oplossing moet zijn, maar ons meteen ook een manier geeft om die oplossing te vinden.
Meteen maar even toepassen op bovenstaand geval:

Voorbeeld 1.    Los op  x ☰ 7 (mod 4) en  x ☰ 12 (mod 5)
x ☰ 7 (mod 4) geeft  x = 7 + y • 4
invullen in de tweede:   7 + y • 4 ☰ 12  (mod 5)
y • 4 ☰ 5 (mod 5)
y ☰ 5 • 4-1 (mod 5)
ggd(4, 5) = 1 dus de inverse z  van 4 (mod 5) bestaat. Die kun je vinden via  4z + 5k = 1 en dat geeft z ☰ 4 (mod 5)
y ☰ 5 • 4 (mod 5)  ☰ 20  (mod 5)
x ☰ 7 + 20 (mod 20)  ☰  27 (mod 20).
       
       

© h.hofstede (h.hofstede@hogeland.nl)