| |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
| 1. |
Als gevolg
van een voedselvergiftiging ligt Robert al enkele dagen in het
ziekenhuis. Zijn lichaamstemperatuur zal volgens de doktoren het
volgende verloop hebben: |
| |
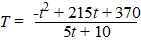 |
| |
|
|
|
| |
waarin
t de tijd in dagen is, gerekend vanaf het moment dat Robert ziek
werd, en T zijn lichaamstemperatuur in °C.
Robert is genezen als zijn temperatuur weer 37°C is |
| |
|
|
|
| |
a. |
Toon met
de afgeleide aan dat de lichaamstemperatuur direct na de vergiftiging
stijgt. |
| |
|
|
|
| |
b. |
Bereken
algebraïsch de maximale temperatuur die wordt bereikt. |
| |
|
|
|
| 2. |
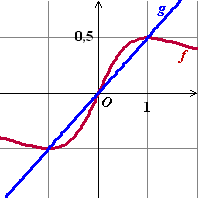
Gegeven zijn de
functies: f(x) = x/(x2
+ 1) en g(x) = 1/2x.
De grafiek
van g lijkt door de toppen van de grafiek van f te gaan |
 |
| |
|
|
| |
a. |
Onderzoek
algebraïsch of dat inderdaad het geval is |
| |
|
|
| |
Tussen
x = 0 en x = 1 worden een aantal verticale lijnstukken tussen
de grafieken van f en g getekend.
Voor de lengte L van zo’n lijnstuk geldt: |
| |
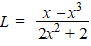 |
| |
|
|
|
| |
b. |
Toon aan
dat deze formule juist is |
|
| |
|
|
|
| |
c. |
Bereken
algebraïsch de maximale waarde van L. Geef je antwoord in twee decimalen |
| |
|
|
|
| 3. |
examenvraagstuk
HAVO Wiskunde B, 1989. |
| |
|
|
|
| |
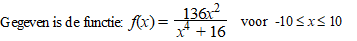 |
| |
De grafiek van die functie is hieronder
getekend. |
| |
|
|
|
| |
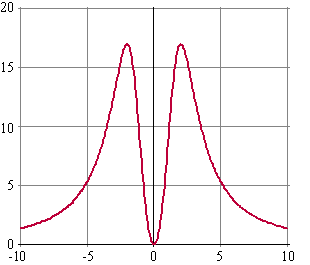 |
| |
|
|
|
| |
a. |
Bereken de kleinste en de
grootste functiewaarde. |
| |
|
|
|
| |
b. |
Los op: f(x)
≥ 8 |
| |
|
|
|
| 4. |
examenvraagstuk
HAVO Wiskunde B, 1990.
|
| |
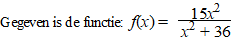 |
| |
In onderstaande figuur is een deel van de grafiek van
f getekend. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Bereken het maximum van f(x) |
| |
|
|
|
| |
b. |
Teken het deel van de grafiek
van f tussen x = -20 en x = 0. Gebruik hierbij
dezelfde schaal als de figuur hierboven. |
| |
|
|
|
| |
De raaklijn aan de grafiek van
f in het punt met x-coördinaat 3 snijdt de y-as
in A |
| |
|
|
|
| |
c. |
Bereken de y-coördinaat
van A. |
| |
|
|
|
| |
d. |
Los op: f(x)
> 3/4 |
| |
|
|
|
| |
Stel a en b zijn
getallen waarvoor geldt: a • b = 36 |
| |
|
|
|
| |
e. |
Bewijs dat f(a)
= f(b) |
| |
|
|
|
| 5. |
examenvraagstuk
VWO Wiskunde B, 2000. |
| |
|
|
|
| |
Voor p > 0 zijn
gegeven de functies: |
|
| |
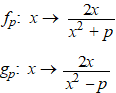 |
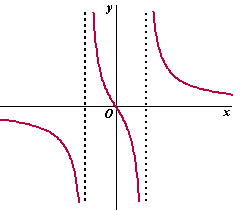 |
| |
Hiernaast is de grafiek van
g1 getekend. |
| |
|
|
| |
a. |
Onderzoek f1 en teken
de grafiek van f1 in de figuur hiernaast. Bepaal
hierbij ook de eventuele snijpunten van de grafieken van f1
en g1. |
| |
|
|
|
| |
Voor elke p > 0
liggen de toppen van de grafiek van fp zowel op de
verticale asymptoten van de grafiek van gp als op
de kromme y = 1/x. |
| |
|
|
|
| |
b. |
Bewijs dit. |
| |
|
|
|
| 6. |
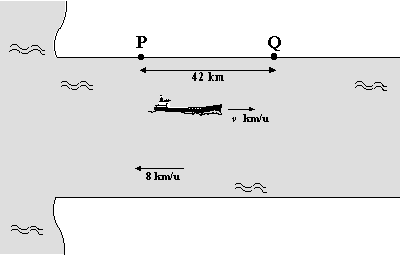
examenvraagstuk
VWO Wiskunde B, 2004.
Een schip maakt een tocht over een rivier
van P naar Q en terug. De afstand tussen P en Q is 42 km. Van P naar Q
vaart het schip tegen de stroom in (stroomopwaarts); op de terugreis
vaart het met de stroom mee (stroomafwaarts).
De snelheid van het schip ten opzichte van de wal hangt af van de
stroomsnelheid van het water en van de snelheid v van het schip
ten opzichte van het water; hierbij is v in km/u. De
stroomsnelheid van het water is 8 km/u. Zie de figuur hieronder, waarin
de tocht van P naar Q is weergegeven. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Veronderstel v = 20. |
| |
|
|
|
| |
a. |
Toon aan dat de tocht van P
naar Q en terug dan 5 uur duurt. |
| |
|
|
|
| |
Het brandstofverbruik B op
het deel van de tocht stroomopwaarts hangt af van de vaartijd T (in
uren) en van de snelheid v (in km/u) van het schip ten opzichte
van het water.
Er geldt B = T • v3.
Voor het deel van de tocht stroomopwaarts geldt:
|
| |
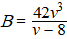 |
| |
|
|
|
| |
b. |
Toon deze laatste formule aan. |
| |
|
|
|
| |
c. |
Bereken algebraïsch bij welke
waarde van v het brandstofverbruik minimaal is voor het deel van
de tocht stroomopwaarts. |
| |
|
|
|
| |
|
| 7. |
examenvraagstuk
VWO Wiskunde A, 2012. |
| |
|
|
|
| |
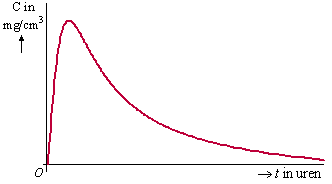
De firma PharmaCie brengt een nieuw medicijn tegen hooikoorts op
de markt. Het nieuwe medicijn van PharmaCie wordt in pilvorm verkocht.
Als een patiënt klachten krijgt, neemt hij een pil. De werkzame stof
komt dan via de maag en de darm in de bloedbaan terecht. De hoeveelheid
werkzame stof in de bloedbaan stijgt eerst en neemt daarna af omdat de
stof door het lichaam wordt afgebroken. De concentratie van de werkzame
stof in de bloedbaan noemen we C.
In de figuur hiernaast zie je een schets van de grafiek van
C. |
 |
| |
Een onderzoeker van PharmaCie stelt de volgende formule
op die dit verloop redelijk benadert: |
| |
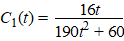 |
| |
Hierin is C1
de concentratie werkzame
stof in mg/cm3
en
t
de tijd in uren na het innemen van
de pil. |
| |
|
|
|
| |
a. |
Bereken met behulp van de afgeleide van
C1
na hoeveel minuten,
gerekend vanaf het moment dat de pil is ingenomen, de concentratie
werkzame stof maximaal is. |
| |
|
|
|
| |
Een andere onderzoeker stelt een geheel andere formule
op die er als volgt uit ziet:
C2(t)
= 0,13(1,92-t - 1,92-6t)
Hierin is C2
de concentratie werkzame
stof in mg/cm3
en
t
weer de tijd in uren na het
innemen van de pil.
Hoewel de grafieken van
C1
en
C2
beide erg op de grafiek in
bovenstaande figuur lijken, verschillen de momenten waarop het maximum
bereikt wordt wel van elkaar.
Voor de afgeleide van
C2
geldt bij benadering:
C'2(t)
= 0,0848(-1,92-t + 6 • 1.92-6t) |
| |
|
|
|
| |
b. |
Onderzoek met behulp van de afgeleide
C'2
of het maximum van
C2
eerder of later dan
het maximum van C1
optreedt. |
| |
|
|
|
| 8. |
examenvraagstuk VWO, Wiskunde B,
1994. |
| |
|
|
|
| |
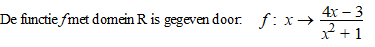 |
| |
Toon aan dat de lijn y =
41/2x
- 3 de grafiek van f zowel snijdt als raakt. |
| |
|
|
|
| 9. |
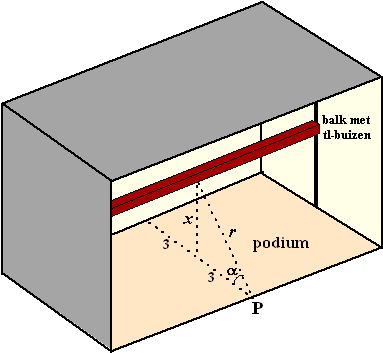
Examenvraagstuk VWO,
wiskunde B, 2007. Een podium is 6 meter diep.
Midden boven het podium hangt een balk met tl-buizen. De
verlichtingssterkte op het podium is het kleinst aan de rand, bijvoorbeeld
in punt P. De afstand van P tot de balk is r meter, de hoogte van
de balk boven het podium is x meter en de hoek die het kortste
verbindingslijnstuk van de balk en punt P met het podium maakt is a
radialen. Zie de volgende figuur. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
De verlichtingssterkte op het
podium in punt P noemen we V (in lux). V is omgekeerd evenredig met r
en evenredig met sina. Dus V = c •
1/r • sina,
waarbij de evenredigheidsconstante c afhangt van het
lichtvermogen van de tl-buizen.
Voor deze balk met tl-buizen geldt: c = 650 (lux•m)
Er geldt:
|
| |
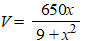 |
| |
|
|
|
| |
a. |
Toon aan dat deze formule juist is. |
|
| |
|
|
|
| |
De balk met tl-buizen kan omhoog
gehesen worden: de hoogte kan variëren van 2,0 tot 5,0 meter.
De verlichtingssterkte op het podium in punt P moet minimaal 100 lux zijn. |
| |
|
|
|
| |
b. |
Bereken langs algebraïsche weg op welke
hoogtes de balk mag hangen. |
| |
|
|
|
| |
c. |
Er is een hoogte van de balk
waarbij V maximaal is. Bereken deze hoogte langs algebraïsche weg. |
| |
|
|
|
| |
|
|
|
| 10. |
Gegeven is de functie
fp door: |
| |
|
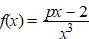 |
| |
|
|
|
| |
a. |
Voor welke p ligt het
buigpunt van de grafiek van f op de lijn y =
x ? |
| |
|
|
|
| |
b. |
De grafiek van g(x)
= a/x raakt aan de grafiek van f4(x).
Bereken a en de coördinaten van het raakpunt. |
| |
|
|
|
| |
c. |
T is het maximum van fp(x)
Voor welke p is de afstand van T tot de oorsprong minimaal?
Geef je antwoord in twee decimalen nauwkeurig. |
| |
|
|
|
| |
|
|
|
| 11.. |
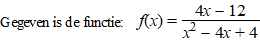 |
| |
|
|
|
| |
De lijn met vergelijking
y = p(x - 3) heeft 3 snijpunten met de grafiek
van f.
Bereken voor welke waarden van p dat het geval is. |
| |
|
|
|
| |
|
|
|
| 12. |
Examenvraagstuk VWO Wiskunde A,
2017-I |
| |
|
|
|
| |
Veel moderne auto’s tonen op het bedieningspaneel
een schatting van het aantal kilometers dat je nog kunt rijden
zonder te tanken.
Dit noem je de actieradius.
Een automobilist zag bijvoorbeeld de informatie van de figuur
hiernaast op zijn bedieningspaneel. Hier is ‘Tot. afstand’ de totale
afstand die de auto tot dat moment heeft gereden. |
 |
| |
De actieradius wordt berekend op basis van:
- de nog aanwezige hoeveelheid benzine in de tank;
- het rijgedrag tot op dat moment. |
|
| |
|
|
|
| |
Toen dezelfde automobilist wat zuiniger ging rijden,
kreeg hij de informatie van de figuur hiernaast te zien.
Zoals je ziet, heeft hij 20 km gereden. Toch is zijn actieradius
niet met 20 km afgenomen, maar slechts met 17 km. Hij is dus
inderdaad iets zuiniger gaan rijden en hij heeft zodoende 3
kilometer ‘gewonnen’. |
 |
| |
|
|
|
| |
De automobilist neemt zich voor om op zekere dag
zijn benzinetank volledig te vullen en dan zo zuinig mogelijk te
gaan rijden. De afstand in km die hij rijdt vanaf het moment dat hij
getankt heeft, noemen we x.
De automobilist houdt de eerste 200 km bij wat er gebeurt met de
actieradius A (in km) op zijn bedieningspaneel. Zie de tabel. |
| |
| x |
0 |
50 |
100 |
150 |
200 |
| A(x) |
625 |
582 |
539 |
496 |
452 |
|
| |
|
|
|
| |
Tussen x =
0 en x = 100 neemt de
actieradius met minder dan 100 km af.
De automobilist ‘wint’ dus kilometers op dit traject. |
| |
|
|
|
| |
a. |
Bereken hoeveel kilometer hij op dit
traject wint door zuinig te rijden. |
| |
|
|
|
| |
De automobilist maakt een wiskundig model bij de
tabel. Hij stelt de volgende formule op: |
| |
|
|
|
| |
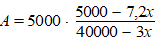 |
| |
|
|
|
| |
Op het moment dat hij begint te rijden met de volle
tank, dus als x =
0 , is de actieradius veel
kleiner dan de afstand die hij in werkelijkheid zal rijden met deze
tankinhoud.
Op het moment dat de tank leeg is, is de actieradius gelijk aan
0. |
| |
|
|
|
| |
b. |
Bereken hoeveel km de automobilist volgens het model
met een volle tank in werkelijkheid méér kan rijden dan het
bedieningspaneel bij vertrek aangaf. |
| |
|
|
|
| |
Dat de automobilist inderdaad kilometers wint, kun
je ook nagaan door het verloop te bekijken van de som S(x)
van het aantal werkelijk gereden kilometers en de actieradius. Als
de automobilist kilometers wint, zal S(x) namelijk
stijgend zijn.
De formule voor S(x) is: S(x) = x
+ A(x) |
| |
|
|
|
| |
c. |
Bepaal de afgeleide van S(x) en laat
met behulp van een schets van de afgeleide zien dat de automobilist
op het traject van x =
0 tot x =
500 voortdurend kilometers wint. |
| |
|
|
|
| |
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |