|
© h.hofstede (h.hofstede@hogeland.nl)
|
|
Meer opgaven |
|
 |
 |
| |
|
|
|
 |
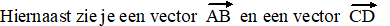
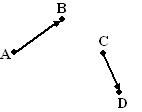
Ik heb lekker geen schaalverdeling gegeven, want je mag geen
berekeningen maken.
Teken ergens in deze figuur de volgende vectoren: |
 |
| |
|
|
|
| |
a. |
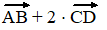 |
| |
|
|
|
| |
b. |
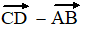 |
| |
|
|
|
| |
c. |
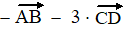 |
| |
|
|
|
| |
b. |
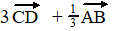 |
| |
|
|
|
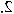 |
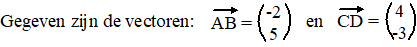 |
| |
Bereken daarmee de kentallen van de
vectoren uit de vorige vraag. |
| |
|
|
|
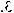 |
Gegeven zijn het punt P(xp,
yp) en Q(xq, yq)
O is de oorsprong.
Geef de kentallen van de volgende vectoren, uitgedrukt in xp,
yp, xq, yq |
| |
|
|
|
| |
a. |
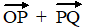 |
| |
|
|
|
| |
c. |
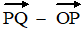 |
| |
|
|
|
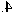 |
Leg uit of de
volgende vectoren evenwijdig zijn of niet |
| |
|
|
|
| |
a. |
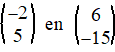 |
| |
|
|
|
| |
b. |
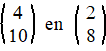 |
| |
|
|
|
 |
Gegeven zijn de
punten A = (3, 10) en B(7, 12)
Punt C ligt op AB zodat AC : CB =
3 : 7
Bereken de coördinaten van punt C |
| |
|
|
|
|
|
| |
|
|
|
| 6. |
Driehoek ABC heeft hoekpunten A(0, 2) en B(3, 6)
en C(10, 0)
P
ligt op zijde AB zodat AP : PB = 2 : 1
Q
ligt op zijde BC zodat BQ : QC = 3 : 1
M is het midden van PQ. Zie de figuur.
Bereken de lengte van lijnstuk AM. |
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|