| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
 |
|
Meer opgaven |
| |
|
|
|
 |
| |
|
|
|
 |
Een jongetje
gooit op t = 0 (t in seconden) een bal van
een toren omhoog weg.
Voor de hoogte h (in m) geldt: h(t) =
60 + 20t - 4,9t2 |
| |
|
|
|
| |
a. |
Welk getal
uit de formule geeft aan dat de bal omhoog gegooid wordt? |
| |
|
|
|
| |
b. |
Bereken de
gemiddelde snelheid van de bal gedurende de vierde seconde. |
| |
|
|
|
| |
c. |
Bereken de
snelheid van de bal na 3 seconden |
| |
|
|
|
 |
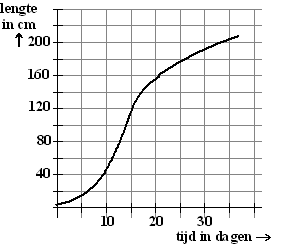
Ik heb een
aantal dagen de hoogte van een zonnebloem in mijn tuin
bijgehouden. De gegevens staan in de grafiek hiernaast.
Beantwoord de volgende vragen met behulp van deze grafiek. |
|
| |
|
|
| |
a. |
Hoe snel groeit de
zonnebloem op t = 10? |
| |
|
|
| |
b. |
Hoe groot was de
gemiddelde groeisnelheid tussen t = 10 en t = 30?
Is er een moment geweest waarop de zonnebloem met deze snelheid
groeide? Zo ja, wanneer, zo nee, waarom niet? |
| |
|
|
|
| |
c. |
Wanneer groeide de
zonnebloem met een snelheid van
4 cm/dag? |
| |
|
|
|
| |
|
|
|
 |
Een sporter wil weten
hoe het met zijn conditie gesteld is.
Hij sprint daarom eerst zo snelmogelijk een rondje op een atletiekbaan
(dat is 400 meter)
Bij de finish aangekomen meet hij een aantal minuten lang zo vaak
mogelijk zijn hartslag. Dat kan hij doen met zijn smartwatch.
Voor die hartslag blijkt de volgende formule te gelden: |
 |
| |
|
|
| |
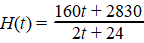 |
| |
|
|
|
| |
Daarin is H de
hartslag in slagen per minuut en t de tijd in seconden vanaf zijn
finish. |
| |
|
|
|
| |
a. |
Bereken algebraïsch
na hoeveel seconden zijn hartslag gelijk is aan 100 slagen per
minuut |
| |
|
|
|
| |
b. |
Als de snelheid
waarmee zijn hartslag afneemt op tijdstip t = 10 vanaf dat moment
constant zou blijven, wanneer is zijn hartslag dan gelijk aan 85
slagen per minuut?
Geef je antwoord in één decimaal nauwkeurig. |
| |
|
|
|
 |
De formule s
= 65√(3t + 4) - 130 geeft de afgelegde
afstand in meter na t seconden.
Op welk interval [2, p] is de snelheid gelijk aan de
snelheid op t = 3?
Geef een algebraïsche berekening en rond p af op één decimaal. |
| |
|
|
|
|
|
| |
|
|
|
| 5. |
Zodra de eerste nachtvorst komt denkt elke
rechtgeaarde Fries uiteraard alleen nog maar aan de
Elfstedentocht. Zo ook Ir. Kroes. Hij roept zijn rayonhoofden
bij elkaar. De vergadering besluit dat de komende winter de
tocht gehouden kan worden bij een ijsdikte van minimaal 17 cm.
Om een goed beeld te krijgen van het weer nemen ze weerman Piet
Paulusma in de arm. Die gooit alle gegevens van de afgelopen
jaren in een enorme computer, en komt tot de conclusie dat er de
komende winter voor de dikte van het ijs zal gelden: |
| |
|
|
|
| |
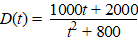 |
| |
|
|
|
| |
Daarin is
D de ijsdikte in cm, en t de tijd in dagen (met t
= 1 op 1 januari). |
| |
|
|
|
| |
a. |
Hoeveel groeit de ijslaag gemiddeld per dag tussen 7
januari en 15 januari? |
| |
|
|
|
| |
b. |
Wanneer zou volgens dit model
de tocht gehouden kunnen worden?
|
| |
|
|
|
| |
c. |
Hoe snel groeit de ijslaag op 8 februari? |
| |
|
|
|
| |
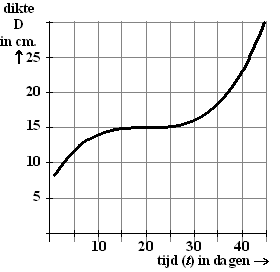
Echter, concurrent
Peter Timofeeff komt met een heel ander model.
Volgens hem zal voor de dikte van de ijslaag gelden:
D(t) = 0,001t3
- 0,06t2
+ 1,2t + 7
Als extra service levert hij de grafiek hiernaast erbij. |
|
| |
|
|
| |
d. |
Bepaal met deze grafiek wanneer de groei van de
ijslaag vanaf t = 1 gemiddeld 0,5 cm/dag
was.
(leg uit). |
| |
|
|
| |
e. |
"Als het ijs zo snel blijft groeien als
vandaag, dan zal het op 9 februari maar liefst 30 cm dik
zijn" roept een enthousiaste Fries (maar dan in het Fries).
Leg uit wanneer hij dat riep. |
| |
|
|
|
| |
f. |
Bereken hoe snel het ijs
volgens dit model groeide op t = 35. |
| |
|
|
|
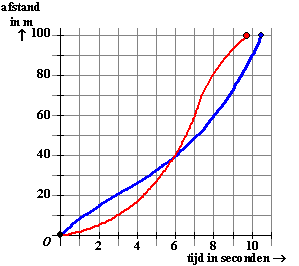
| 6. |
Twee
honderd-meter lopers, ROOD en BLAUW, lopen een wedstrijd
tegen elkaar. De grafieken van de afgelegde afstand als functie
van de tijd staan in de figuur hiernaast. |
|
| |
|
|
| |
a. |
Benader de snelheid van
ROOD op t = 4. |
| |
|
|
| |
b. |
Wanneer liep BLAUW met
een snelheid van 12 m/s? |
| |
|
|
| |
De formule A = 0,1t3
- t2 + 9t blijkt de
grafiek van BLAUW erg goed te beschrijven (A de afstand, t
de tijd). |
| |
|
|
|
| |
c. |
Controleer met deze
formule of je antwoord op vraag b. klopt. |
| |
|
|
|
| |
d. |
Met welke snelheid finishte BLAUW? |
| |
|
|
|
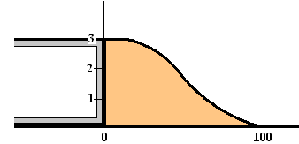
| 7. |
In de figuur hiernaast staat een dwarsdoorsnede van een viaduct
met afrit. De hoogte van deze afrit wordt gegeven door:
h = 0,000006·x3 – 0,0009·x2 +
3
Hierin zijn x en h in meter en is het assenstelsel zoals
getekend.
In de dwarsdoorsnede is te zien dat de lengte van de afrit in
horizontale richting gemeten 100 meter is, en dat de hoogte van het
viaduct 3 meter is.
|
 |
| |
|
|
|
| |
a. |
Bereken bij welke x
de hoogte van de afrit nog maar 50 cm is.
|
| |
|
|
|
| |
b. |
Bereken hoe steil de
afrit daalt bij x = 20
|
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|