© h.hofstede (h.hofstede@hogeland.nl)

Meer opgaven
       
       
Los algebraïsch op:  
         
  a. √(x + 6) = x f. 2√x - x = -15
         
  b. 2 - 3√(x) =  x - 16 g. √(4 - x) = x + 8
         
  c. -5√(2x + 1) = -12 h. 2x + 2 = 2√x + x + 10  
         
  d. x + 1 = 3 + √x i. x - √x = 30
         
  e. √(6 - 5x) + x = 2 j. √(1 + √x) = 4
         
Kleine Laurens groeit als een wortel.
Letterlijk in dit geval, want zijn lengte L wordt gegeven door: 
L = 16 • √(t + 9)
daarin is t in maanden met t = 0 als tijdstip van zijn geboorte, en L in cm. 
       
  a. Welke invloed heeft het getal 9 op de grafiek van L?
       
  b. Bereken algebraïsch wanneer Laurens 100 cm lang zal zijn. Rond je antwoord af op twee decimalen.
       
  Op de geboortedag van Laurens heeft  zijn trotse vader een boompje in de tuin geplant. Dat boompje was toen 60 cm hoog. Het boompje groeit lineair en zal na twee jaar 69,6 cm hoog zijn. Laurens is dan langer dan het boompje.
       
  c. Hoeveel procent is Laurens op dat moment langer dan het boompje?
       
  d. Stel een formule op voor de lengte van het boompje en bepaal daarna op welk tijdstip Laurens en het boompje even lang zijn.
       
examenvraagstuk HAVO Wiskunde B, 2002.

In de figuur hiernaast zijn de grafieken getekend van de functies
 f (x) = √(-2x + 12) 
en  g(x) = x - 1

     
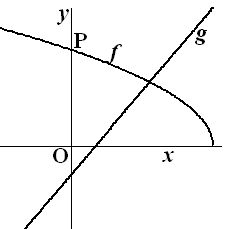  a. Los op  f(x)  ≤  g(x). Rond de getallen in je antwoord die niet geheel zijn af op twee decimalen.
     
  De verticale lijn x = a snijdt de grafiek van  f  in punt S en de grafiek van g in punt T; S ligt boven T.
     
  b. Onderzoek voor welke waarde van a de lengte van ST gelijk is aan 2. Geef je antwoord in twee decimalen nauwkeurig.
     
MEER OPGAVEN
       
4. examenvraagstuk HAVO Wiskunde B, 2002.

De functie f is gegeven door:  
 f(x) = √(x2 − 6x) 
voor x ≤ 0 en voor x ≥ 6.

De functie g is gegeven door
g(x) = x − 2 .
In de figuur hiernaast zijn de grafieken van f en g getekend.

Toon op algebraïsche wijze aan dat de grafieken van f en g geen snijpunt hebben.

       
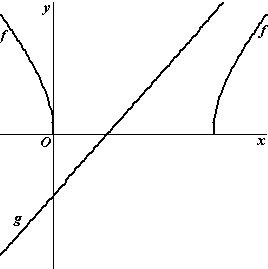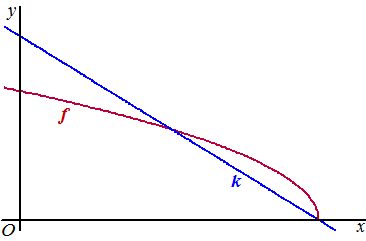
5. examenvraagstuk HAVO wiskunde B, 2016-I

 De functie f  is gegeven door f (x) = √(−3x + 6) .  Lijn k heeft vergelijking   y = -7/4 • x + 7/2  
In onderstaande figuur zie je de grafiek van f en lijn k.
       
 

       
  Lijn k gaat door het gemeenschappelijk punt van de grafiek van f met de x-as.
       
  a. Toon dit op algebraïsche wijze aan.
       
  b. Lijn k en de grafiek van f  hebben nog een ander punt gemeenschappelijk.
Bereken in twee decimalen nauwkeurig de x-coördinaat van dit punt.
       
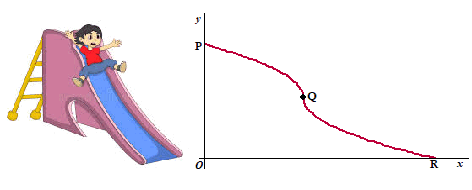
6.

De meeste glijbanen zijn nogal saai, zoals in de figuur linksonder.
Ik besluit een leukere glijbaan te ontwerpen….
Die staat in de figuur rechtsonder. Hij heeft bij punt Q een spectaculaire daling. 
       
 

       
  Als ik de oorsprong kies zoals in de figuur, dan voldoen de twee delen van mijn

glijbaan aan de volgende vergelijkingen:  

PQ:  y = 1 + 0,5√(3 - x)
QR:  y = 1 - 0,5√(x - 3)

Daarin zijn de afstanden gegeven in meters. In punt Q sluiten de twee delen van de glijbaan op elkaar aan.
       
  a. Voor welke x is de glijbaan hoger dan  1,60 meter?   Geef een algebraïsche berekening.
       
  b. Bereken algebraïsch de hoogte van punt Q.
       
  c.

Hoe ontstaat de grafiek van QR uit de grafiek van  y = Öx?
       
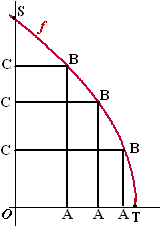
7. Gegeven is de functie  f(x) = √(1 - 2x)
In de figuur hiernaast  is de grafiek van f getekend.

Het punt B doorloopt de grafiek van f tussen T en S; de punten A en C zijn steeds de projecties van B op respectievelijk de x-as en de y-as. Als B niet met S of met T samenvalt, is OABC een rechthoek. Die rechthoek verandert voortdurend van vorm. Er is één plaats van B waarbij OABC een vierkant is.

Bereken de coördinaten van die plaats.

       
8. Vlaamse Olympiade.

Welk van de volgende vergelijkingen heeft/hebben  precies één oplossing?

a.  1 = √t + √(1 - t)
b.  2 = √t + √(2 - t)
c.  3 = √t + √(3 - t)
d.  4 = √t + √(4 - t)
e.  5 = √t + √(5 - t)
       
9. examenvraagstuk HAVO Wiskunde B, 2021-II.

De functie f is gegeven door
 

       
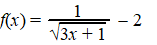  De grafiek van f snijdt de x-as in punt A en de y-as in punt B. Zie de figuur.

       
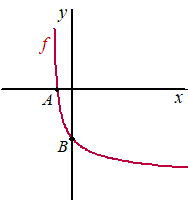10. Sanaslank is een nieuwe manier om gewicht te verliezen, gebaseerd op een dieet zonder koolhydraten.
Men ontwikkelt voor iedere deelnemers aan het dieet een persoonlijke formule van de volgende vorm:
       
 

  Daarin is
•  W het gewicht (in kg) na t dagen,
•  B het begingewicht (t = 0 is het moment dat men aan het dieet begint),
•  A de hoeveelheid (in kg) die men af wil vallen,
•  S de streeftijd (aantal dagen) waarin dit moet gebeuren.
       
  a. Een man van 80 kg wil volgens dit dieet in 50 dagen tijd 10 kg afvallen.
Bereken algebraïsch na hoeveel dagen hij 75 kg zal wegen.
       
  b. Een vrouw van 60 kg gaat in 20 dagen 5 kg afvallen, en ontwikkelt de volgende formule:
t = aW2 + bW + c
Bereken de constanten a, b en c in deze formule.
       
     

© h.hofstede (h.hofstede@hogeland.nl)