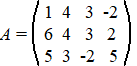© h.hofstede (h.hofstede@hogeland.nl)

Tweepersoons-nulsomspel.
       
Dat zijn spellen met twee personen (duh) waarbij de totale uitbetaling nul,mis. Dat betekent dat de winst van de ene speler automatisch het verlies van de andere is.
Zo' n spel kun je daarom eenvoudig weergeven met een uitbetalingsmatrix.
Neem bijvoorbeeld de volgende matrix die de uitbetaling van speler 1 (S1) weergeeft.
       

       
De drie rijen geven elk één van de mogelijke keuzes van S1 aan, en de vier kolommen geven elk één van de mogelijke keuzes van S2 aan.
Het getal op de kruising geeft de winst voor S1 (dus het verlies van S2)
Als S1 bijvoorbeeld voor de tweede strategie kiest en S2 voor de vierde, dan is de uitbetaling 2 voor S1
       
S1 kan ervoor zorgen een bepaalde minimale gegarandeerde winst te halen.
- Als hij rij 1 kiest is zijn minimale winst -2
- Als hij rij 2 kiest is zijn minimale winst 2
- Als hij rij 3 kiest is zijn minimale winst -2
Door rij 2 te kiezen kan S1 zich verzekeren van een minimale winst (van 2).
Dit noemen we een maximin-strategie (hij kiest het maximum van de minima van de rijen)
Deze minimale winst (2 in dit geval) noemen we wA (winst van A)
       

wA = maxi(minj(aij))

       
Op dezelfde manier kan S2 zijn verlies beperken tot een maximaal verlies:
-  Als hij kolom 1 kiest is zijn maximale verlies 6
- Als hij kolom 2 kiest is zijn maximale verlies 4
- Als hij kolom 3 kiest is zijn maximale verlies 3
- Als hij kolom 4 kiest is zijn maximale verlies 5
Door kolom 3 te kiezen kan S2 zich verzekeren van een maximaal verlies (van 3)
Dir noemen we een  minimax-strategie (hij kiest het minimum van de maxima van de kolommen)
Dit maximale verlies (3 in dit geval) noemen we vA (verlies van A)
       

vA = minj(maxi(aij))

       
Stelling:      vA   ³   wA
Bewijs: 
  Voor iedere k geldt: aik ³ minj aij voor iedere i.
immers minaij is de kleinste uit rij i  en aik is een willekeurig element van rij i
Daaruit volgt dat:   maxi aik ³  maxi (minj aij ) = wA
vA = mink (maxiaik) ³  maxi (minj aij ) = wA
q.e.d.      
       

       
Dominerende rijen en kolommen.
       

Als aij ³ akj voor alle j, dan zal S1 geen interesse hebben in rij k, immers elk getal uit rij i is hoger.
Dus kan rij k net zo goed uit de matrix worden weggelaten, immers die zal toch nooit gekozen worden.
We zeggen dan dat rij  i de rij k domineert.

Analoog geldt: als aij  £ ail  voor alle i, dan is kolom l voor S2 niet interessant en kan deze kolom worden weggelaten. Op deze wijze kan de matrix worden gereduceerd totdat er geen dominante rijen of kolommen meer zijn.

Bovenstaande matrix A zou dan bijvoorbeeld teruggebracht kunnen worden tot:
       

       
       
       

© h.hofstede (h.hofstede@hogeland.nl)