| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
 |
|
Vergelijkingen met logaritmen |
| |
|
|
|
| Om logaritmische
vergelijkingen op te lossen zijn er eigenlijk twee mogelijkheden: |
| |
|
|
|
| 1. Maak ervan
glogx = a dan volgt
daar direct uit x = ga |
|
| |
|
|
|
| 2. Maak ervan glog(a)
= glog(b) dan mag je de
glog weglaten dus dan geldt a =
b |
|
| |
|
|
|
Wat je eigenlijk bij
beide methoden doet is van beide kanten van de vergelijking g.....
te nemen. Een soort balansmethode, maar dan met
tot-de-macht. Door dat g..... valt dan die
glog weg.
Van beiden maar even een voorbeeld: |
| |
|
|
|
Voorbeeld 1: Los op:
2 • 3logx + 3log(2x)
= 4
Oplossing:
2 • 3logx + 3log(9x)
= 4
3log(x2) + 3log(9x)
= 4 (rekenregel uit de vorige les)
3log(9x3) = 4
(rekenregel uit de vorige les)
9x3 = 34 = 81 (beide
kanten tot-de-macht-3 nemen)
x3 = 9
x = 91/3 |
|
| |
|
|
|
Voorbeeld 2:
Los op: 2logx = 2log(x
- 1) + 2log(5)
Oplossing:
2logx = 2log(x
- 1) + 2log(5)
2logx = 2log((x
- 1)×5))
(rekenregel uit de vorige les)
x = 5(x -
1) (beide
kanten tot-de-macht-2 nemen)
x = 5/4 |
|
| |
|
|
|
Bedenk goed dat de
grondtallen wel steeds gelijk moeten zijn.
Wat je moet doen als dat niet zo is zien we in een volgende les.
Een gewoon getal is ook een log! |
| |
|
|
|
Om beide kanten van
een vergelijking te kunnen schrijven als glog(....) is
het soms handig om van gewone getallen ook logaritmen te maken.
Dat is gelukkig erg makkelijk als je maar bedenkt dat glogx
en gx elkaars omgekeerde zijn.
Zo is 3log(32) gelijk aan 2 omdat die
macht en die log elkaar opheffen
En ook 5log(54) = 4 en 2log(213)
= 13 en ga zo maar door.
Dus andersom kun je van een gewoon getal erg makkelijk een logaritme
maken:
3 = 7log(37) en 3,5 = 4log(43,5)
enz, |
| |
|
|
|
|
|
| |
|
|
|
|
Denk om het domein! |
| |
|
|
|
In de vorige les
zagen we dat logaritmen alleen bestaan als het deel onder de log
positief is.
Dat betekent dat je de antwoorden van je oplossingen altijd moet
controleren.
De antwoorden die de logaritme van een negatief getal opleveren vallen
af. |
| |
|
|
|
Voorbeeld 3: Los
op: 5log(x) + 5log(2x)
= 2 + 5log(0,5x)
Oplossing:
5log(x) + 5log(2x)
= 2 + 5log(0,5x)
5log(2x2) = 2 + 5log(0,5x)
5log(2x2) = 5log(52)
+ 5log(0,5x)
5log(2x2) = 5log(12,5x)
2x2 = 12,5x
2x2 - 12,5
= 0
x(2x - 12,5) = 0
x = 0 ∨ x = 6,25
Maar x = 0 valt af want dat geeft log(0) en dat
bestaat niet.
De oplossing is dus x = 6,25. |
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
Los algebraïsch op: |
| |
|
|
|
|
| |
a. |
4 + 2 ×
3logx = 15
- 3log(9x) |
d. |
1 + 4log(3x) = 2 ×
4log(x) |
| |
|
|
|
|
| |
b. |
1/2
• 2log(x) = 2log(x)
- 2log7 |
e. |
0,5log(x - 1) =
0,5log(x) - 2 |
| |
|
|
|
|
| |
c. |
2 • log(x) = 2 + log(x
+ 24) |
f. |
3 + 2log(x + 4) = 2log(x
+ 80) |
| |
|
|
|
|
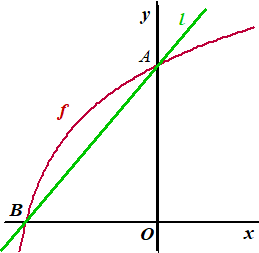
| 2. |
De functie f
is gegeven door f(x) = 2log(x
+ 8).
De grafiek van f snijdt de x-as in punt B en de
y-as in punt A.
Verder is l de lijn door A en B.
Zie de figuur.
Stel op algebraïsche wijze een
vergelijking op voor
l. |
 |
| |
|
|
|
|
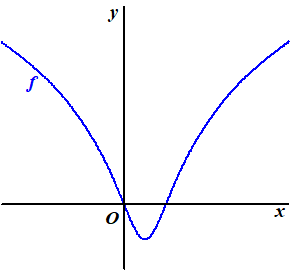
| 3. |
De functie f wordt gegeven door:
f(x) = 3log(2x2
-
2x
+ 1)
In de volgende figuur is de grafiek van f weergegeven |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
De grafiek van f lijkt geen verticale
asymptoot te hebben. De grafiek van de standaardfunctie y =
3log(x)
heeft wél een verticale
asymptoot. |
| |
|
|
|
|
| |
a. |
Bewijs dat de grafiek van f
inderdaad geen verticale asymptoot heeft. |
| |
|
|
|
|
| |
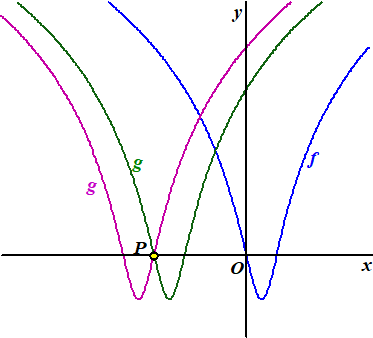
Gegeven is het punt P(-3, 0)
De grafiek van f wordt over een afstand p naar links verschoven. Hierdoor ontstaat de grafiek van de
functie g.
Er zijn twee waarden van p waarvoor de grafiek van g
door P gaat. Zie onderstaande figuur. |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
b. |
Bereken exact deze twee waarden van
p. |
| |
|
|
|
|
| 4. |
Elk jaar hebben we
weer vaak last van vliegende mieren.
Ze lijken zomaar ineens met z'n allen ergens in de lente te verschijnen,
maar zijn dan ook weer ineens in de herfst verdwenen.
Een bioloog stelt voor het aantal vliegende mieren in een bepaald gebied
het volgende model op:
M(t) = 1500 ×
3log(400t
- t2 -
30000) |
 |
| |
|
|
|
|
| |
Daarin is t de
tijd in dagen (met t = 0 op 1 januari) en M het aantal
vliegende mieren per km2 in het gebied.
De formule geldt uiteraard alleen voor zover M positief is. |
| |
|
|
|
|
| |
a. |
Voor welke waarden
van t is de formule geldig? Geef je antwoord in dagen nauwkeurig. |
| |
|
|
|
|
| |
b. |
Bereken algebraïsch wanneer er 12000 mieren per km2 in het
gebied zijn. |
| |
|
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|