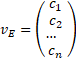© h.hofstede (h.hofstede@hogeland.nl)

Lineaire afbeeldingen.
       
Een afbeelding tussen twee vectorruimten V en W is één of ander recept dat een element van V koppelt aan een element van W. Erg interessant zijn afbeeldingen tussen twee vectorruimten V en W die de structuur van die ruimten intact laten.
Dat soort afbeeldingen heten lineaire afbeeldingen (ook wel  homomorfismen)  en ze voldoen aan de volgende twee eisen:
       
een lineaire afbeelding  f:  V  → W  is een afbeelding waarvoor geldt:
 
  1.  f(x + y) = f(x) + f(y)
  2.  f(c • x) = c • f(x)
   
       
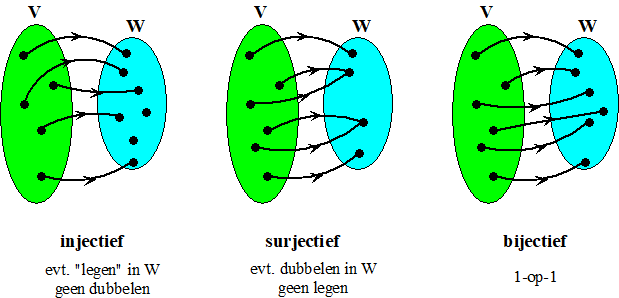
Daar volgt direct de volgende simpele eigenschap uit:   f(c1 • x + c2 • y) = c1 • f(x) + c2 • f(y)
Ik zal je niet beledigen door dit te gaan bewijzen......
Een lineaire afbeelding is dus een afbeelding die lineaire combinaties omzet in lineaire combinaties. 

En op dezelfde manier volgt (bijna triviaal)  dat  f(0) = 0

De volgende stellingen zijn ook erg eenvoudig te bewijzen. Doe het zelf maar als oefening.

Stelling 1.   Als f :  V → W  en  g :  W → X  lineaire afbeeldingen zijn, dan is   g o f :  V → X  ook een lineaire afbeelding
Stelling 2:   Als  f, g :  V → W lineaire afbeeldingen zijn, dan zijn  (f + g):  V → W  en   (cf ) : V → W ook lineaire afbeeldingen

De volgende twee alinea's lijken verdacht veel op elkaar. Ze gaan over Kern en Beeld van een afbeelding.

De kern van een afbeelding.

De kern van een afbeelding f  (genoteerd als ker( f )) bestaat uit alle vectoren uit V die op 0 worden afgebeeld. Denk erom dat dit niet het getal 0, maar het nulelement van vectorruimte W is.

Stelling:   Voor een lineaire afbeelding  f :  V → W  is  ker(f ) een deelruimte van V.

Bewijs.
Neem een willekeurige v en w uit ker( f )
Als f(v) = 0, dan is  f(c • v) = c • f(v) = c • 0 = 0  dus  ker(f) is gesloten onder de scalaire vermenigvuldiging.
Als  f(v) = 0 en f(w) = 0 dan is  f(v + w) = f(v) + f(w) = 0 + 0 = 0  dus ker(f) is gesloten onder de optelling.
f(0) = 0  dus  0 zit in ker(f).
Dat waren de drie eisen die we aan een deelruimte stelden.

De kern van een afbeelding heeft nogal veel te maken met het feit of een afbeelding injectief is of niet.
Een afbeelding f :  V → W is injectief als  twee verschillende elementen van V nooit hetzelfde beeld in W hebben

Dan zijn de volgende drie uitspraken gelijk voor lineaire afbeeldingen f :  V →  W
 

f  is  injectief
⇔
ker(f) = {0}
⇔
het beeld van een stelsel lineaire onafhankelijke vectoren in V 
is lineair onafhankelijk in W

       
Bewijzen.
(1) ⇒ (2):   omdat f(0) = 0 en elk beeld maar hoogstens één origineel kan hebben is 0 het enige element van V dat op 0 wordt afgebeeld. Dus is {0) de kern van f

(2) ⇒ (1):   Stel f(v) = f(w)  Dan is  f(v - w) = f(v) - f(w) = 0  dus zit v - w in ker(f). Maar omdat ker(f) alleen maar {0} is, is dus  v - w = 0 . Dus is  v = w.  Dus is f  injectief.

(2) ⇒ (3):   Stel dat het stelsel {v1, v2, ..., vn}  onafhankelijk is.
Als dan   c1f(v1) + c2f(v2) + ... + cnf (vn) = 0  dan is  f(c1v1 + c2v2 + ... +  cnvn ) = 0  (f is immers lineair)
Dus is   c1v1 + c2v2 + ... +  cnvn = 0  (want dan zit die in de kern van f)
Maar omdat {v1, v2, ..., vn}  onafhankelijk is volgt daaruit dat  c1 = c2 = ... = cn = 0
Als de rode vergelijking volgt uit de blauwe dan is het stelsel  {f (v1), f(v2), ..., f(vn)}  onafhankelijk.

(3) ⇒ (2):  Als  v ≠  0, dan is het ministelsel {v} onafhankelijk in V. Dus volgens (3) is dan het ministelsel {f(v)} onafhankelijk in W, dus is  f(v) ≠ 0 dus geen enkele vector die ongelijk aan nul is kan op nul worden afgebeeld. Dus de kern bestaat alleen uit {0},  immers f(0) = 0 geldt wel.

(1) ⇒ (3)  want  (1) ⇒ (2)  en  (2) ⇒ (3)
(3) ⇒ (1)  want  (3) ⇒ (2)  en  (2) ⇒ (1)

q.e.d.

Het beeld van een afbeelding.

Het beeld van een afbeelding  f:  V → W  bestaat uit alle vectoren van W die een origineel in V hebben. Het zijn als het ware alle vectoren van W die "bereikt" worden door afbeelding f op alle vectoren van V toe te passen.  We geven het beeld van f aan met  Im(f).

Stelling:   Voor een lineaire afbeelding  f :  V → W  is  Im(f ) een deelruimte van W.
f(v) + f(w) = f(v + w)  en ligt dus in Im(f)
c • f(v) = f(cv)  en ligt dus in Im(f)
f(0) = 0 ligt in Im(f)
Dat waren de drie eisen die we aan een deelruimte stelden.

Het beeld van een afbeelding heeft nogal veel te maken met het feit of een afbeelding surjectief  is of niet.
de afbeelding f : V → W is surjectief als elke vector uit W het beeld is van een vector uit V.

Dan zijn de volgende drie uitspraken gelijk voor lineaire afbeeldingen f :  V →  W
 

f  is surjectief
⇔
Im(f) = W
⇔
Als Span(A) = V  dan is  Span(f(A)) = W

       
Bewijzen.

(1) ⇒ (2).  Dûh!
(2) ⇒ (1).  Dûh!

 Stel A = {a1, a2, ...}  is een deelverzameling van V, dan is een willekeurige vector a  uit Span(A) te schrijven als 
a = c1 • a1 + c2 • a2 + ...
 
f(Span(A)) =
=  f (c1 • a1 + c2 • a2 + ...)
=  f(c1 • a1)  + f(c2 • a2) +...
= c1 • f (a1)  + c2 • f (a2) + .... 
= Span(f(A))

(2) ⇒ (3)
Als Span(A) = V  dan is  Im(f) =  f(V) =  f(Span(A))  = ... = Span(f(A)) en dat is dan volgens (2) gelijk aan W

(3) ⇒ (2)
Als Im(f) = W dan is  f(V) = W en als  Span(A) = V dan wordt dat dus  f(Span(A)) = Span(f(A)) =W


Laten we de laatste twee alinea's samenbrengen:

Bijecties en Isomorfismen.

Een bijectie is een afbeelding die tegelijkertijd injectief en surjectief is. Een bijectie wordt ook wel een 1-op-1 afbeelding genoemd, omdat aan elk element van V precies één element van W wordt gekoppeld. Een bijectieve lineaire afbeelding heet ook wel een isomorfisme. Twee vectorruimtes waartussen een isomorfisme bestaat heten dan ook isomorf.
       

       
Stelling:
 

Als f:  V → W een isomorfisme is,  dan is het beeld van elke basis in V weer een basis in W.
       
Bewijs.

Dat volgt direct uit de vorige twee stellingen.
Als f  injectief is, dan is het beeld van een basis in V een stelsel onafhankelijke vectoren in W.
Als f  surjectief is, dan geldt  span(A) = V ⇒  span(f(A)) = W  dus het beeld van een basis brengt de hele ruimte W voort.
Het beeld van een basis is dus onafhankelijk en volledig, dus weer een basis.

Een bijectieve afbeelding  f  van V naar W heeft ook een inverse afbeelding f -1 van W naar V.  Draai in het rechterplaatje hierboven alle pijlen gewoon om.

Stelling:
 

De inverse f -1 van een isomorfisme f  is weer een isomorfisme.
       
Bewijs.
Dat f -1 een bijectie is weten we al  (omgekeerd 1-op-1 is natuurlijk weer 1-op-1) dus we moeten alleen nog aantonen
dat f -1 lineair is:
f -1(v + w) = f -1(f (f -1(v) + f(f -1(w)))
= f -1(f  (f -1(v) + f -1(w)))       maar f -1 na f toepassen levert niets op
=  f -1(v) + f -1(w)

f -1(cv) =  f -1 (f (f -1(cv)))
= f -1 (f (cf -1(v)))
= cf -1(v)

Dus de afbeelding is ook lineair.

En nu naar echte vectoren...

Kies een basis  E = {e1, e2, ..., en} van de n-dimensionale vectorruimte V.  Als we de vectoren daarvan nummeren en ze altijd in de gegeven volgorde weergeven spreken we van een geordende basis  (tot nu toe was een basis slechts een verzameling zonder orde of volgorde).
Een willekeurige vector v uit V kun je nu schrijven als  v = c1e1 + c2e +  ... + cnen  en dat kan op precies één manier.
Die  c1, c2, ...cn  noemen we vanaf de coördinaten van v ten opzichte van basis E.
We noteren ze voortaan als:

       
Je moet dit eigenlijk zien als een afbeelding die een vector v op een serie getallen afbeeldt:  fE(v) = {c1, c2,..., cn}
Op deze manier wordt een vector uit een n-dimensionale vectorruimte bij een gegeven geordende basis  gekoppeld aan een serie van n  geordende getallen. Dat betekent dat alle (eindige) vectorruimten door hun dimensie worden geclassificeerd. Alle ruimten met dezelfde dimensie zijn isomorf met elkaar!! 't Is allemaal één pot nat!!!
       
       
   OPGAVEN
       
1. We hebben de volgende afbeelding f verzonnen, die een 2  × 2 matrix afbeeldt op een reëel getal:
       
 

       
  Onderzoek of dit een lineaire afbeelding is.
       
       
       
       
       
       
       

© h.hofstede (h.hofstede@hogeland.nl)