| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Lijnintegralen. |
| |
|
|
|
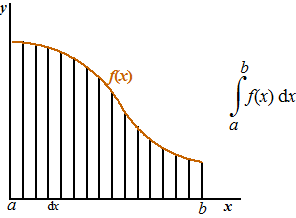
| Helemaal in het begin
zagen we een integraal als de som van een groot aantal rechthoekjes: |
| |
|
|
|
|
 |
| |
|
|
|
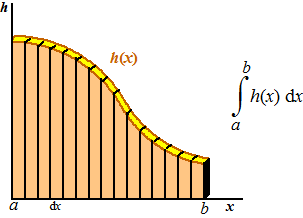
| 't Is alsof je de
oppervlakte berekent van een schutting die langs de x-as staat en
hoogte h(x) heeft: |
| |
|
|
|
|
 |
| |
|
|
|
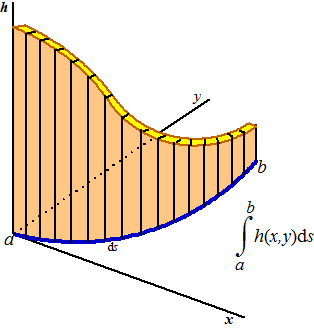
Maar ja; Waarom
zouden we ons beperken tot zo'n stijve kaarsrechte schutting?
Waarom niet een wat moderner ontwerp?
Zoiets moois als dit bijvoorbeeld: |
| |
|
|
|
|
 |
| |
|
|
|
(Ik heb de tweede as
op de bodem maar weer y genoemd).
In plaats van die saaie x-as gebruiken we nu die blauwe kromme.
Dat betekent dat er twee veranderingen in de integraal zijn:
1. De hoogte h hangt nu af van de plaats op de blauwe lijn,
dus van x én van y.
2. De stukjes dx zijn nu stukjes ds geworden.
Laten we kijken wat de gevolgen zijn...... |
| |
|
|
|
1. h
is een functie van x én van y.
Dat betekent dat er onder die integraal x-en en y-en
staan, en het probleem is dat ik niet weet hoe je dat moet primitiveren.
Gelukkig hebben we een extra voorwaarde; we weten namelijk dat
(x, y) op de blauwe bodemlijn moet liggen.
Stel bijvoorbeeld dat h(x, y) = x
- y2 en dat die blauwe bodemlijn de
lijn y = x2 is.
De integraal wordt dan: |
|
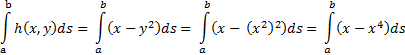 |
| |
|
|
|
| |
|
|
|
2. dx
is ds geworden.
|
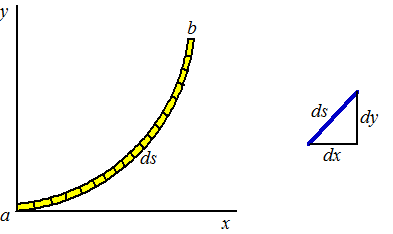
Nou moet die ds
nog veranderen in dx.
Hiernaast zie je een bovenaanzicht van de situatie.
Als de ds nou maar klein genoeg genomen wordt, dan kun je zo'n
stukje ds als een recht lijntje benaderen.
Dan geldt (Pythagoras):
ds2 = dx2
+ dy2
|
 |
|
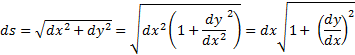 |
Die dy/dx
is natuurlijk gewoon de afgeleide van y.
In bovenstaand voorbeeld zou de integraal dan worden: |
| |
|
|
|
|
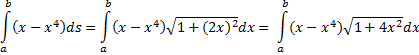 |
| |
|
|
|
| Nou voor a en
b nog even de x-waarden nemen en klaar! Het is nu
een "gewone" integraal geworden. (wel een moeilijke trouwens:
primitiveren zal wel niet lukken; dit is typisch een karweitje voor de
Grafische Rekenmachine). |
| |
|
|
|
Voorbeeldje.
Bereken de integraal van h(x, y) = 2xy
+ 1 langs de kromme y = x + x3
tussen de punten (1, 0) en (2, 10) |
| |
|
|
|
|
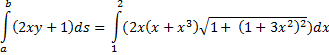 |
| De GR geeft ongeveer
164,09. |
| |
|
|
|
|
De bodemkromme als een
parametervoorstelling. |
| |
|
|
|
Natuurlijk kan die
blauwe bodemkromme ook gegeven zijn als een parametervoorstelling.
Als je daar nog een beetje verstand van hebt zul je al wel snappen wat
we gaan doen: |
| |
|
|
|
|
|
| |
|
|
|
Vervang dus de x
en y in de functie h(x, y) door hun t-vergelijking
en neem als grenzen de t-grenzen.
Die ds gaat als volgt: |
|
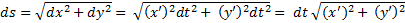 |
| Daarbij zijn die x'
en y' dus afgeleiden naar t. |
| |
|
|
|
| Voorbeeldje.
Bereken de integraal van h(x, y) = 2x + y
over het ellipsdeel dat gegeven wordt door:
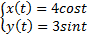 |
| Tussen t = 0
en t = 1/2π. |
|
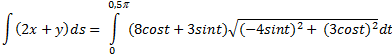 |
| De GR geeft ongeveer
28,62. |
| |
|
|
|
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| 1. |
Een komeet volgt een hyperboolbaan
met vergelijking x2 - y2
= 1 langs een zon.
De aantrekkingskracht die de zon op de komeet uitoefent is
F = c/r2
waarbij r de afstand van de zon tot de komeet is, en c
een constante.
Neem voor het gemak c = 1, en bereken de hoeveelheid
arbeid die de zon op de komeet uitoefent tijdens het deel van de
baan waarvoor y > 0. |
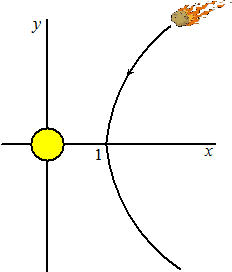 |
| |
|
|
|
| |
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|