| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Verbanden vergelijken |
 |
| We hebben in de loop
van de wiskundelessen al heel wat verschillende formules met elk hun
speciale eigenschappen en grafieken gezien. Deze les maken we een
overzicht van wat we allemaal al weten.
1. Lineair. |
| |
|
|
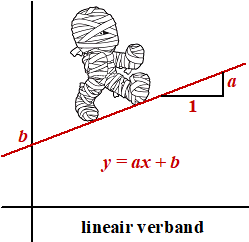 |
De formule hierbij is
y = ax + b
De grafiek is een rechte lijn.
• b is het beginpunt (op de y-as)
• a is het hellinggetal: bij 1 stap naar rechts gaat
de lijn a omhoog.
Als b = 0 gaat de lijn door de oorsprong en dan heet dit ook wel
een recht-evenredig verband. |
|
2. Exponentieel. |
| |
|
|
|
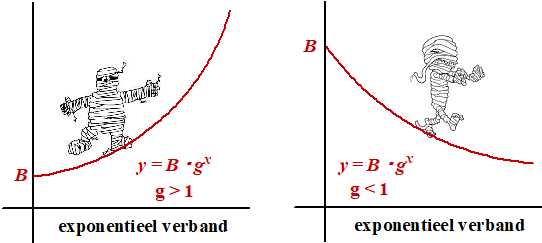
De formule is
y = B • gx
De grafiek heeft toenemende stijging (als g > 1) of afnemende
daling (als g < 1)
• B is het begingetal (op de y-as)
• g is de groeifactor.
Voor berekeningen kun je gebruiken dat ga • gb
= ga + b en (ga)b
= gab |
| |
|
|
|
|
 |
| |
|
|
|
|
3. Machten. |
| |
|
|
|
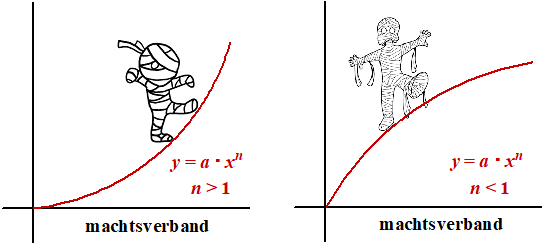
De formule is
y = a • xn
De grafiek stijgt. Toenemende stijging als n > 1 en
afnemende stijging als n < 1
De grafiek gaat door de oorsprong.
Voor berekeningen kun je gebruiken dat an • bn
= (ab)n |
| |
|
|
|
|
 |
| |
|
|
|
|
4. Wortels. |
| |
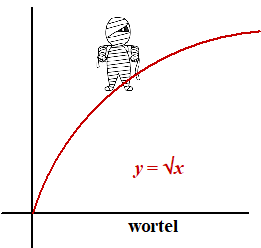 |
De formule is
y = √x
Dit is eigenlijk ook een machtsverband, want √x = x0,5
De grafiek heeft een randpunt.Voor berekeningen kun je
gebruiken dat √a • √b = √(ab)
|
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
Iemand warmt in 25
minuten een hoeveelheid water op van 5 °C
naar 100 °C. |
| |
|
|
|
| |
a. |
Bereken hoeveel
graden het water is na 10 minuten verwarmen als de temperatuut lineair
toeneemt. |
| |
|
|
|
| |
b. |
Bereken hoeveel
graden het water is na 10 minuten verwarmen als de temperatuur
exponentieel toeneemt. |
| |
|
|
|
| 2. |
Een psychologe doet
onderzoek naar de snelheid waarmee kinderen woordjes leren. Zij
laat een groep kinderen elke dag een half uur dezelfde woordjes
leren, en test na elke dag hoeveel woordjes de leerlingen
gemiddeld kennen. Dat geeft de volgende tabel: |
| |
|
|
|
| |
| dag (d) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| gem. woordkennis (W) |
18,5 |
29,6 |
39,0 |
47,5 |
55,3 |
62,6 |
69,5 |
|
| |
|
|
|
| |
a. |
Leg duidelijk uit hoe
je kunt zien dat hier GEEN sprake is van een exponentieel verband. |
| |
|
|
|
| |
De psychologe gaat uit
van een machtsverband W = a • db
Als dat inderdaad zo is, dan kun je direct zien dat moet gelden a
= 18,5 |
| |
|
|
|
| |
b. |
Leg duidelijk uit hoe je dat kunt
zien. |
|
| |
|
|
|
| |
De psychologe vindt aan
de hand van bovenstaande tabel dat b = 0,68. |
| |
|
|
|
| |
c. |
Leg met een berekening uit hoe je dat
getal zelf zou kunnen vinden. |
| |
|
|
|
| |
d. |
Na hoeveel dagen zal
W gelijk zijn aan 150? |
| |
|
|
|
| 3. |
Examenopgave HAVO
Wiskunde A, 2022-I
De CO2-concentratie in de lucht
blijft toenemen. In 2000 was het jaargemiddelde 369,5 ppm, in 2015
was dit opgelopen tot 400,8 ppm.
Tibbe vermoedt op basis van de figuur bovenaan deze opgave dat
het jaargemiddelde in de periode 2000–2015 groeide volgens een
exponentieel verband en dat de groei zich in de jaren daarna
voortzet volgens hetzelfde exponentiële verband. Je kunt dan,
uitgaande van bovenstaande gegevens, berekenen in welk jaar het
jaargemiddelde voor het eerst hoger dan 500 ppm zal zijn. |
| |
|
|
|
| |
a. |
Bereken op deze
manier in welk jaar het jaargemiddelde voor het eerst hoger dan 500
ppm zal zijn. |
| |
|
|
|
| |
Marrit is het
niet eens met Tibbe: zij vermoedt dat er vanaf het jaar 2000 geen
sprake is van exponentiële groei, maar van lineaire groei. Je kunt
dan, uitgaande van de jaargemiddelden van 2000 en 2015 en met behulp
van lineair extrapoleren, berekenen in welk jaar het jaargemiddelde
voor het eerst hoger dan 500 ppm zal zijn. |
| |
|
|
|
| |
b. |
Bereken op deze
manier in welk jaar het jaargemiddelde voor het eerst hoger dan 500
ppm zal zijn. |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|