translaties

	© h.hofstede (h.hofstede@hogeland.nl)
Veranderen van grafieken.

De grote vraag vandaag is "Wat gebeurt er met de formule die bij een grafiek hoort, als je de grafiek verandert?"

We bekijken deze les 3 verschillende gevallen:

1. Omhoog of omlaag verschuiven.

2. Naar links of naar rechts verschuiven.

3. De afstand tot de x-as veranderen.

Geval 1. Omhoog of Omlaag verschuiven.

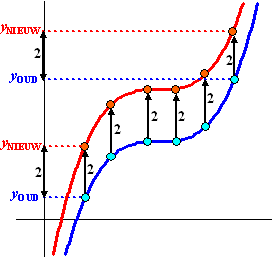
Laten we als voorbeeld een grafiek bekijken die 2 omhoog wordt geschoven. Zie de figuur hiernaast.
De blauwe grafiek wordt 2 omhoog geschoven.
Dat betekent dat alle rode punten 2 hoger liggen dan hun blauwe partners. Alle zwarte pijlen hebben dus lengte 2.
Op de y-as zie je bij twee zulke koppeltjes dat dan geldt dat y_NIEUWook 2 hoger ligt dan y_OUD. Dus:

y_NIEUW = y_OUD + 2

Maar de y is eigenlijk de uitkomst van de hele formule, dus staat hier eigenlijk: NIEUWE FORMULE = OUDE FORMULE + 2

En wat voor 2 geldt, geldt natuurlijk voor elk getal.
Conclusie:

Grafiek a omhoog schuiven ⇒ f(x) wordt f(x) + a

En als de grafiek a omláág wordt geschoven dan wordt dat natuurlijk f(x) - a maar dat snapte je waarschijnlijk al wel.

Geval 2: Naar links of naar rechts schuiven.

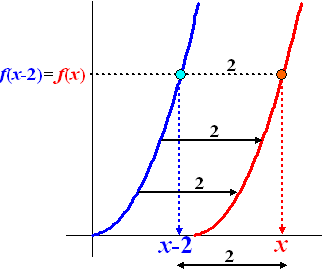
Laten we als voorbeeld een grafiek bekijken die 2 naar rechts wordt geschoven. Zie de figuur hiernaast. De blauwe grafiek gaat over in de rode.
Bekijk nu een punt van de nieuwe grafiek bij de rode x.
De y-waarde die daarbij hoort is dan f_NIEUW(x).
Maar in de figuur zie je dat dat de y van de blauwe grafiek is, die hoort bij x - 2, dus dat is f_OUD(x - 2)

Conclusie: f_NIEUW(x) = f_OUD(x - 2)
In woorden: je krijgt het nieuwe functievoorschrift van de verschoven grafiek door in het oude de x te vervangen door x - 2.
En wat voor 2 geldt, geldt natuurlijk voor elk getal.

Je kunt het ook zo beredeneren:

Als je x vervangt door (x - 2), dan moet je van de x die je wilt invullen eerst 2 aftrekken. Dus om dezelfde y-waarde als bij de oorspronkelijke grafiek te vinden, moet x dan juist 2 groter zijn.

Conclusie:

grafiek a naar rechts schuiven ⇒ elke x vervangen door (x - a)

• Het zal je niet verbazen dat je de grafiek a naar links kunt schuiven door in de formule x te vervangen door (x + a).
• Als er meerdere x-en in de formule staan moet je ze allemaal vervangen door (x ± a)

Geval 3: De afstand tot de x-as een aantal keer zo groot maken.

Dat je getallen kunt vermenigvuldigen dat wist je natuurlijk wel, maar wist je ook dat je een grafiek kunt vermenigvuldigen?
Ja?
Echt waar?
Opschepper!

Een punt vermenigvuldigen is makkelijk.

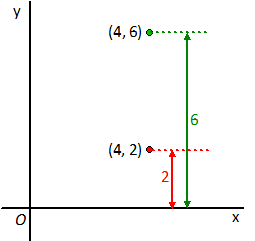
Kijk maar hiernaast.

Daar is het punt (4, 2) vermenigvuldigd ten opzichte van de x-as met een factor 3.
Dat betekent niets anders dan dat de afstand tot de x-as 3 keer zo groot is gemaakt.
Dan komt (4, 2) dus terecht in (4, 6)

En als je een hele grafiek moet vermenigvuldigen dan vermenigvuldig je gewoon alle punten stuk voor stuk.
Dat heeft tot gevolg dat de afstand van de hele grafiek tot de x-as drie keer zo groot wordt.

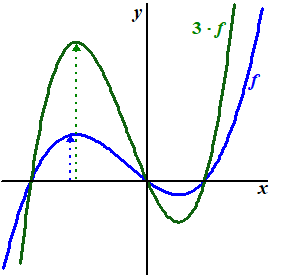
Hieronder zie je een voorbeeld van een grafiek die wordt vermenigvuldigd ten opzichte van de x-as met factor 3.

Wat zijn de gevolgen voor de formule?

Die is niet zo moeilijk: dan wordt de afstand van elk punt tot de x-as a keer zo groot. Maar die afstand tot de x-as dat is de y!!!!
Dus elke y wordt a keer zo groot. Dat betekent dus dat de hele formule (dat ís immers y) met a wordt vermenigvuldigd.

afstand tot de x-as a keer zo groot
⇒ vermenigvuldig de hele formule met a

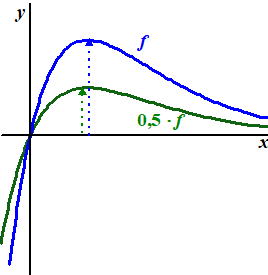
En als de factor a kleiner dan 1 is, dan wordt de afstand tot de x-as dus juist kleiner in plaats van groter. Hieronder zie je een grafiek die met een factor ¹/₂ t.o.v. de x-as wordt vermenigvuldigd.

OPGAVEN


1.	Geef de vergelijking van de functies die in de volgende gevallen ontstaan. Schrijf je formule in de vorm y = ax² + bx + c

	a.	De grafiek van y = 2x² - 6x + 8 wordt 4 naar rechts geschoven.

	b.	De grafiek van y = 6 - 8x² wordt 5 naar links en daarna 4 omlaag geschoven.

	c.	De grafiek van y = 4x + x² wordt 2 naar links geschoven en vervolgens wordt de afstand tot de x-as 3 keer zo groot gemaakt.

	d.	De grafiek van y = x² wordt eerst 4 omlaag geschoven, daarna wordt de afstand tot de x-as gehalveerd en tenslotte wordt de grafiek 2 naar links geschoven.

2.	Als je de lijn y = 2x + 4 over een afstand 3 naar rechts schuift krijg je precies dezelfde grafiek als wanneer je hem 6 omlaag schuift. Toon dat aan!

3.	Examenvraagstuk HAVO Wiskunde B, 2023-II De functie f wordt gegeven door f(x) = x³ + 6x² - 36x - 88. Door de grafiek van f twee naar rechts te verschuiven ontstaat de grafiek van de functie g. Een formule voor g is g(x) = x³ - 48x.

	a.	Bewijs dat dit een formule is voor g.

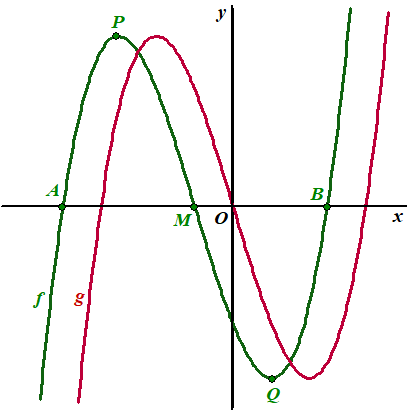
	In de volgende figuur zijn de grafieken van f en g weergegeven.



	Het middelste snijpunt van de grafiek van g met de x-as ligt in de oorsprong. De grafiek van f heeft behalve punt M nog twee snijpunten met de x-as: het punt A en het punt B. De coördinaten van die snijpunten zijn met de functie f moeilijk te berekenen. Met behulp van de functie g zijn de coördinaten van deze snijpunten wel te berekenen.

	b.	Bereken exact de x-coördinaten van A en B.

4.	Je kunt van de grafiek van y = x³ + 2x de afstand tot de x-as twee keer zo groot maken en daarna de grafiek 5 omlaag schuiven. Je kunt ook de grafiek eerst 5 omlaag schuiven en daarna de afstand tot de x-as twee keer zo groot maken. Leg duidelijk uit waarom deze beide manieren niet dezelfde eindgrafiek opleveren.