© h.hofstede (h.hofstede@hogeland.nl)

Rekenen met Logaritmen.
Natuurlijk willen we ook graag vergelijkingen met logaritmen gaan oplossen. Maar daarvoor moeten we eerst wel een idee hebben hoe je met logaritmen om moet gaan.
Eιn basisregelregel hebben we al:
   
gx = a   ⇒  x = glog a
   
Maar welke regels zijn er om bokvoorbeeld logaritmen bij elkaar op te tellen of met elkaar te  vermenigvuldigen?
Kun je verschillende logaritmen misschien samennemen?

De vraag van vandaag:
   

Hoe maak je berekeningen met logaritmen? 

   
Laten we een paar mogelijke bewerkingen met logaritmen bekijken.
glog a + glog b =  ?
Van deze  eerste rekenregel voor logaritmen zal ik een bewijs geven.

Omdat je g log weg kunt krijgen door de inverse g-tot-de-macht erop toe te passen gaan we maar eens proberen beide kante van deze vergelijking g-tot-de-macht te nemen:

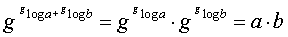
·  Bij de eerste stap hebben we een rekenregel van machten gebruikt.
·  Bij de laatste stap hebben we gebruikt dat g-tot-de-macht en  g-log  elkaar opheffen, daarom komt er a • b uit.
Maar wat staat hier nou eigenlijk?
Er staat   g? = a • b  maar daaruit volgt dan weer  ? = glog(a • b)
maar dat ?  was  gloga + glogb, dus we vinden de formule: 
gloga  + glogb = glog (ab)
   
Denk erom dat de regel alleen geldt als de grondtallen van de logaritmen gelijk zijn!!!

Dat samennemen van die twee logaritmen kun je handig gebruiken om vergelijkingen op te lossen.
   
Voorbeeld:    Los op:   3log(x) + 3log(5) =  2

Oplossing: 
3log(x) + 3log(5) = 2
3log(5x) = 2   (met de nieuwe regel uit deze les)
5x = 32 = 9   (met de regels uit de vorige les.
x = 9/5
   
Er zijn nog meer regels om te rekenen met logaritmen af te leiden. Hier volgen de regels; als je er zin in hebt kijk dan vooral naar de bewijzen.
   

gloga - glogb  =  glog(a/b)
 

glog an  =  n • glog a
 
Van beiden maar een voorbeeldje:
   
Voorbeeld :    Los op:    5log(12) =  5log(4) + 3

Oplossing:
5log(x) =  5log(4) + 3
5log(x) - 5log(4) = 3
5log(x/4) = 3
x/4 = 53 = 125
x = 500
   
Voorbeeld:      Los op:  3 Χ 2log(x) + 2log(0,5x)  - 5 = 0  

Oplossing:
2 Χ 2log(x) + 2log (0,5x) - 5 = 0
2 Χ 2log(x) + 2log(0,5x) = 5
2log(x2) + 2log(0,5x) = 5
2log(0,5x3) = 5
0,5x3 = 25 = 32
x3 = 64
x = 4
   
 
 
OPGAVEN
1. Schrijf als ιιn logaritme, en zo eenvoudig mogelijk:
           
  a. 3log(2) + 3log(5) = f. 2log3 + 4 • 2log5 =
           
  b. 5·logx + 2·logx = g. 2 • 3logx + 3log8 =
           
  c. 0,5 · 2logx - 2logx = h. 5log(x + 1) - 5log(x) =
           
  d. 0,5logx + 0,5log(2x) - 0,5log(3x) = i. 3 • logx + 2 • log4 =
           
  e. -4logx - 4log(x2) = j. 0,5log(x2) + 2 • 0,5log(2x) =

 
2. Zoals je misschien wel weet is  8! (spreek uit:  "acht faculteit") gelijk aan  8 • 7 • 6 • 5 • 4 • 3 • 2 • 1 = 40320
De rekenmachine heeft er zelfs een knop voor:  MATH - PRB - !
Het probleem is echter dat de grootste faculteit die je kunt uitrekenen gelijk is aan 69! (dat is  69 • 68 • ...• 1). Daarna worden de antwoorden groter dan 10100  en dat kan onze rekenmachine niet aan.

Als je je realiseert dat  70! = 70 • 69 • ... • 1 = 70 • 69!  dan kun je 70! uitrekenen door logaritmen te gebruiken:  log(70!) = log(70 • 69!) = log(70) + log(69!) = 1,84509804 + 98,233307 = 100,078405
Dus 70! = 10100,0789405 = 10100 • 100,0789405 = 1,197 • 10100  

Bereken op deze manier 74!
         
3. Als log x = 1/2 en  log y = 6 bereken dan algebraοsch  log(100 • x4/√y)
         
   

© h.hofstede (h.hofstede@hogeland.nl)