| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Meer opgaven |
 |
 |
| |
|
|
|
 |
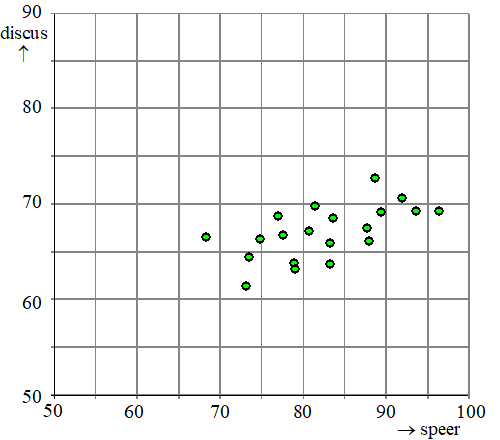
Hieronder staan van een grote groep atleten de resultaten van de
onderdelen speerwerpen en discuswerpen. De afstanden zijn in meters |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Op welk onderdeel was
de gemiddelde afstand het grootst? Leg uit! |
| |
|
|
|
| |
b. |
Op welk onderdeel was
de standaardafwijking het grootst? Leg uit! |
| |
|
|
|
| |
c. |
Hoeveel procent van
de atleten had met de discus minstens 10 meter minder dan met de speer? |
| |
|
|
|
 |
Een gewichtheffer
traint 4 dagen per week in de sportschool. omdat hij een pasje heeft
waarmee hij kan binnenkomen en ook weer weggaan weet hij dus elke keer
precies van hoe laat toe hoe laat hij in de sportschool is geweest.
Echter al die tijd is geen pure trainingstijd. Hij moet eerst omkleden,
dan een warming-up doen. Daarna vindt de werkelijke training plaats en
na afloop daarvan moet hij ook weer een cooling-down doen en douchen en
omkleden.
In het onderstaande actiediagram zie je een actiediagram dat weergeeft
hoeveel tijd de sporter bij een bepaalde training in de sportschool
doorbracht en hoe lang de werkelijke trainingstijd was. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
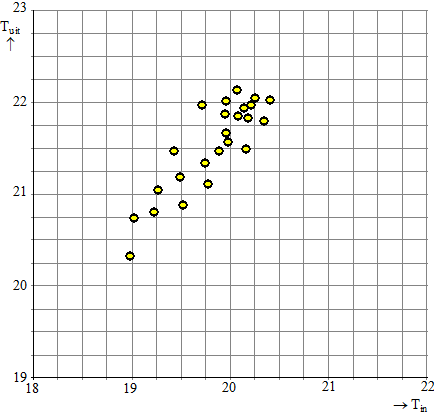
De sporter heeft een groot aantal van zijn actiediagrammen geanalyseerd.
Hij heeft onder anderen gezocht naar een verband tussen het tijdstip van
binnenkomst in de sportschool Tin
en het tijdstip van verlaten van de
sportschool
Tuit
. Daartoe zijn
Tin
en
Tuit
weergegeven in een spreidingsdiagram.
Zie de volgende figuur. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Geef in de figuur aan welk punt
in het spreidingsdiagram afkomstig is van het actiediagram van
de sporter in de eerste figuur. |
| |
|
|
|
| |
b. |
Van deze sporter is de spreidingsbreedte van
Tuit
… keer zo groot als de spreidingsbreedte
van Tin
.
Bereken welk getal er op de puntjes moet staan. Geef
je antwoord in één decimaal. |
| |
|
|
|
| |
Op grond van het spreidingsdiagram trekt de sporter de volgende twee conclusies:
I: Er lijkt bij hem een
verband te zijn tussen
Tin
en
Tuit
.
II: De verdeling van de tijdstippen
Tin
lijkt bij hem niet op een
normale verdeling. |
| |
|
|
|
| |
c. |
Geef bij elke conclusie een geldig argument dat de sporter gebruikt zouden kunnen hebben ter onderbouwing van die
conclusie. |
| |
|
|
|
| |
Zoals we hierboven al zagen is niet alle tijd die in de sportschool
wordt doorgebracht echte trainingstijd. Bij deze sporter is gebleken dat
hij om minstens 1 uur echte trainingstijd te hebben, minstens 1,5 uur
in de sportschool moet doorbrengen. |
| |
|
|
|
| |
d. |
Bepaal met het spreidingsdiagram hoeveel trainingen de sporter
minder dan 1 uur echte trainingstijd heeft gehad. |
| |
|
|
|
 |
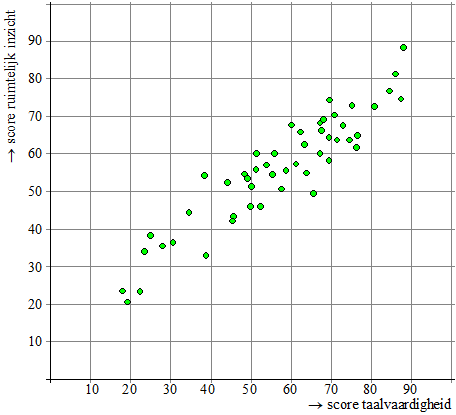
De meeste goede
IQ-tests bestaan uit meerdere onderdelen waarvoor een aparte score
gehaald kan worden. Van 50 IQ-tests staan hieronder de scores die door
de deelnemers zijn gehaald op de onderdelen "taalvaardigheid" en
"ruimtelijk inzicht". Elke stip geeft één deelnemer weer. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Bij het
spreidingsdiagram worden de volgende uitspraken gedaan over de
resultaten van deze 50 IQ-teste: |
| |
I. |
Meer dan 85% van de
deelnemers had een score op ruimtelijk inzicht onder de 70. |
| |
II. |
De mediaan van de
scores op taalvaardigheid is ongeveer 55. |
| |
III. |
De drie hoogste
scoren op de taalvaardigheid zijn ook de drie hoogste scoren op
ruimtelijk inzicht. |
| |
|
|
|
|
|
Onderzoek van
elke uitspraak of deze juist is of onjuist. |
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|