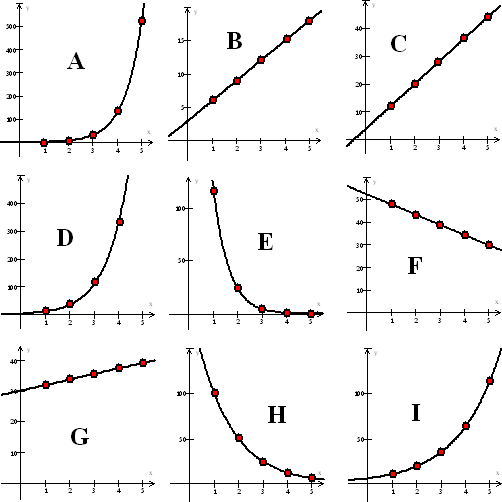Vermenigvuldigingsfactoren.
Laten we beginnen met een eenvoudig IQ-testje.
In elke IQ-test zitten wel een aantal vragen van de categorie "Wat is de volgende in de rij?"
Hier zijn een aantal zulke rijtjes.
Kun je het volgende getal noemen?
A    2   -    8   -   32   -   128   -   512   -   .....
B    6   -   9   -   12   -   15   -   18   -   ....
C    12   -   20   -   28   -   36   -   44   -   ....
D    12   -   36   -   108   -   324   -   972   -   ....
E    120   -   24   -   4,8   -   0,96   -   0,192   -   .....
F    48   -   43,5   -   39   -   34,5   -   30   -   ....
G    32   -   33,8   -   35,6   -   37,4   -   39,0   -   ....
H    100   -   50   -   25   -   12,5   -   6,25   -   ....
I    10,8   -   19,44   -   34,992   -   62,9856   -   ....  
IQ-TEST :  Geef het volgende getal in elk van bovenstaande rijen getallen.
 

2048,  21,  52,  2916,  0.0384,  25.5,  40.8,  3.125, 113.37408
   
VRAAG:  Als je bovenstaande rijen in twee categorieën zou moeten indelen, hoe zou je dat dan doen?
Misschien wordt er iets duidelijk als we de grafieken plotten van deze rijtjes.
Stel dat het eerste getal de y is die hoort bij x = 1, het tweede getal de y die hoort bij x = 2, enz.
Het eerste rijtje zou dan deze tabel geven:
x 1 2 3 4 5
y 2 8 32 128 512
En daar kun je een grafiek van maken.
Als je de negen grafieken hierboven zou plotten krijg je zoiets:

De twee categorieën lijken me duidelijk: er zijn kromme grafieken en er zijn rechte grafieken.
ADEHI horen bij elkaar en ook BCFG.

Waar zit hem dat in?

Dat komt omdat er in de rijen van de kromme grafieken steeds vermenigvuldigd wordt, en in de rijen van de rechte grafieken steeds opgeteld.
JA MAAR...
Wie goed heeft opgelet zal nu zeggen:  "Ja maar bij F wordt niet opgeteld maar afgetrokken en bij  H en E wordt niet vermenigvuldigd maar gedeeld".
Dat klopt, maar wiskundig gezien zijn optellen en aftrekken eigenlijk hetzelfde!!! 
En vermenigvuldigen en delen ook!!!!
Kijk maar:  
Bij F was het steeds -4.5 maar ergens 4.5 van aftrekken is hetzelfde als het negatieve getal -4.5 er bij optellen!  48 - 4.5  =  48 + (-4.5)
En op dezelfde manier is bij E:  120 : 5  = 120 • 0,2  (delen door 5 is vermenigvuldigen met 1/5)
Kortom: we hebben twee systemen op de markt: het OPTELSYSTEEM en het VERMENIGVULDIGSYSTEEM.
   
Dat optelsysteem ken je natuurlijk al:  aan de rechte lijnen hierboven zag je uiteraard direct dat die horen bij een lineaire formule. Dat vermenigvuldigsysteem is nieuw!!
   
Een standaardformule voor vermenigvuldig-systemen.
   
Eerst even wat namen.....:
  •  Het vermenigvuldiggetal noemen we voortaan de GROEIFACTOR:  g
  •  Een vermenigvuldig-systeem noemen we voortaan  EXPONENTIEEL
  •  De waarde bij x = 0  noemen we voortaan de BEGINWAARDE:  B
   
B en g bepalen helemaal hoe de getallen eruit zullen zien. Immers B zegt waar je moet beginnen (welke y hoort bij x = 0) en g zegt hoe elke y ontstaat uit de vorige (waar je mee moet vermenigvuldigen).
Neem bijvoorbeeld  B = 100 en g = 0,9  dan vind je:
 
y(0) = B = 100, 
y(1) = 10 • 0,9 = 90
y(2) = 90 • 0,9 = 81
y(3) = 81 • 0,9 = 72,9
enz.
Maar als je nu  y(14) wilt uitrekenen dan is dat wel vrij veel werk. Kan dat niet handiger?
Kunnen we ook in één keer een y bij een bepaalde x uitrekenen zonder alle tussenliggende waarden te moeten berekenen?
Dat zou een boel tijd schelen.
Voor y(14) zou je de volgende tabel krijgen (de waarden zijn afgerond)
   

   
Als je de tussenliggende getallen in deze tabel weglaat, dan krijg je:
   

   
Daaruit is te zien dat  100 • 0,9 • 0,9 • 0,9 • 0,9 • 0,9 • 0,9 • 0,9 • 0,9 • 0,9 • 0,9 • 0,9 • 0,9 • 0,9 • 0,9 = 23
en daar staat 14 keer 0,9.
Dan geldt dus  100 • 0,914 = 23

BINGO!

Zo kun je elke y uitrekenen.
We hebben gebruikt  23 = y  en  100 = B  en  0,9 = g  en  14 = x
Met letters krijgen we de basisformule:

y = B • gx
Een erg belangrijke formule. De basisformule voor exponentiële processen.

Voorbeeld:  Geef de exponentiële formule die hoort bij de volgende tabel;
   
x 120 121 122 123
y 5,3826 5,4902 5,6000 5,7120
   
De factoren zijn achtereenvolgens  5,4902/5,3826 = 1,02 en   5,6000/5,4902 = 1,02  en   5,7120/5,6000 = 1,02
De groeifactor is dus g = 1,02 en de formule is  y = B • 1,02x
Vul bijv.  (120, 5,3826)  in:  
5,3826 = B • 1,02120 
⇒  5,3826 = B • 10,765  
⇒  B = 5,3826/10,7652 = 0,5
De formule is dus  y = 0,5 • 1,02x
   
 
 
OPGAVEN
   
1. Geef een exponentiële formule die hoort bij de volgende tabellen:
   
 
Tabel A
x 3 4 5 6 7
y 9,60 13,45 18,82 26,35 36,90
Tabel B
x 3 4 5 6 7
y 0,173 0,104 0,062 0,037 0,022
     
 
Tabel C
x -8 -7 -6 -5 -4
y 0,025 0,051 0,102 0,203 0,406
Tabel D
x 2 3 4 5 6
y 0,5 1,9 7,7 30,7 122,9
   
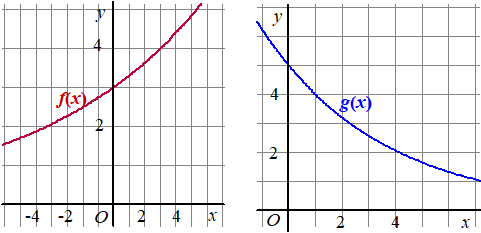
2. Geef een exponentiële formule die hoort bij de volgende grafieken
   
 

   
3. De luchtdruk neemt af met de hoogte.  De volgende tabel geeft daar informatie over:
   
 
hoogte in m 0 1000 2000 3000 4000 5000 6000 7000 8000
luchtdruk in mb 1013 897 793 702 621 550 487 431 381
   
  Neem aan dat de luchtdruk (P, in mb) een exponentiële functie is van de hoogte h (in duizenden meters).
Geef dan het functievoorschrift van deze formule en bereken daarmee op welke hoogte de luchtdruk 300 mb zal zijn geworden.
   
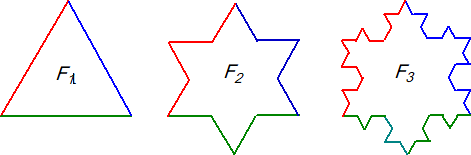
4. Kijk eens naar de volgende rij figuurtjes, daar zit een mooie regelmaat in:
   
 

   
  Wat van figuur 1 naar 2 gebeurt, dat gebeurt overal! Je vindt steeds de volgende figuur door elke lijnstuk van de vorige te vervangen door 5 nieuwe lijnstukjes zoals in figuur 2 voor het eerst is gebeurd.
Als je alsmaar zo doorgaat krijg je steeds gecompliceerdere vorm, en die heet een fractal.
De eerste figuur heeft  lijnstukjes van lengte 15.
Deze is heel beroemd en heet de sneeuwvlok van Koch en ziet er zó uit (mooi ingekleurd):
   
 

   
  a. Stel een formule op voor het aantal zijdes in figuur nummer Fn
       
  b. Stel een formule op voor de lengte van een lijnstukje van figuur nummer n
       
  c. Stel een formule op  voor de totale lengte van alle lijnstukjes samen van figuur nummer n en toon aan dat die totale lengte exponentieel toeneemt.