| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Evenredig |
 |
Soms gaan dingen
"gelijk op"
Daar bedoel ik mee, dat als de één 10 keer zo groot wordt, dan wordt de
ander dat ook. En als de één 5 keer zo klein wordt, dan wordt de ander
dat ook.
Dat heet in de wiskunde
recht-evenredig.
Paar simpele voorbeeldjes van dingen die recht evenredig zijn: |
| |
|
|
|
| |
Ik koop een aantal
flessen wijn, elk voor 6,50. De totale kosten (K) voor die flessen wijn
zijn recht evenredig met het aantal gekochte
flessen (A). |
| |
Jolanda krijgt in een
sponsorloop 3,40 per heel rondje dat zij loopt. Haar totale opbrengst (O)
is recht evenredig met het aantal hele rondjes (n) dat
zij loopt. |
|
|
Op vakantie op een
camping betaal ik 45,- per nacht. Het bedrag (B) dat ik
uiteindelijk moet betalen is recht evenredig met het aantal; dagen (d)
dat ik op de camping sta. |
| |
|
|
|
Berekeningen met recht-evenredige
verbanden.
Met recht-evenredige verbanden kun je op twee manieren een berekening
maken.
1. Met een verhoudingstabel.
Op de eerste plaats kun je een verhoudingstabel maken.
Stel dat de rente die ik op een bankrekening krijg recht evenredig is
met het bedrag dat erop staat. Als ik weet dat ik bij een bedrag van
450,- precies 9,- rente krijg, hoeveel rente krijg is dan voor
1240,-?
Nou, om dat te berekenen maak je de volgende verhoudingstabel: |
| |
| bedrag |
450 |
1240 |
| rente |
9 |
?? |
|
| |
|
|
|
?? = 1240 90/450
= 24,80
2. Met een formule. |
| |
|
|
|
|
Bij een recht-evenredig verband hoort
de formule y = a x |
|
| |
|
|
|
Daarbij is a
een constant getal.
Bij de drie voorbeelden hierboven horen de formules: K =
6,5 A en O = 3,40 n en
B = 45 d
Laten we dezelfde vraag nog eens beantwoorden:
Stel dat de rente die ik op een bankrekening krijg recht evenredig is
met het bedrag dat erop staat. Als ik weet dat ik bij een bedrag van
450,- precies 9,- rente krijg, hoeveel rente krijg is dan voor
1240,-?
Noem de rente R en het bedrag B, dan geldt R
= a B
9 = a 450 geeft dan a =
0,02 dus de formule is R = 0,02 B
B = 1240 geeft dan R = 0,02 1240 =
24,80.Ik hoop dat je ziet dat y = a x
gewoon de formule van een lineair verband is (y =
ax + b) met als enige voorwaarde
dat b = 0
Daarom geldt voor de grafiek van een recht-evenredig verband: |
| |
|
|
|
|
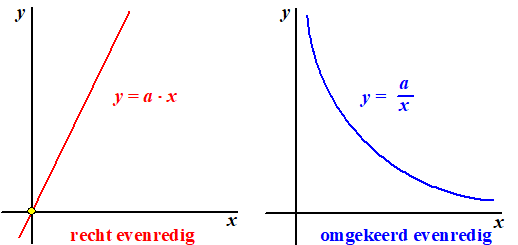
De grafiek van een recht-evenredig
verband is een rechte lijn door (0,0) |
|
| |
|
|
|
Omgekeerd evenredig.
Het zal je niet verbazen dat het bij een
omgekeerd evenredig verband precies omgekeerd gaat!
Als de ene nu 5 keer zo groot wordt, dan wordt de andere juist 5 keer zo
klein. Ze gaan nu niet gelijk op, maar juist tegengesteld.
Paar simpele voorbeeldjes van dingen die omgekeerd-evenredig zijn: |
| |
|
|
|
| |
Guusje gaat op zijn
verjaardag 1200 gram snoep gelijk verdelen over alle kinderen op zijn
feestje die komen. De hoeveelheid snoep (S) die iedereen krijgt
is omgekeerd evenredig met het aantal kinderen (k) dat
er is. |
| |
De elektrische
weerstand (R) van een stroomdraad is omgekeerd evenredig met de
oppervlakte van de doorsnede (O) van die draad. |
|
|
Een grote schutting
langs een stuk snelweg moet worden geschilderd. Eén schilder zou daar 40
uur over doen.
Als er meer schilders (die even snel schilderen) samen aan zouden werken
dan is er een evenredig verband tussen het aantal schilders (s)
en de benodigde tijd (t) |
| |
|
|
|
|
Berekeningen met
omgekeerd-evenredige verbanden. |
| |
|
|
|
|
Bij een omgekeerd-evenredig verband
hoort de formule y
= a/x |
|
| |
|
|
|
Daarbij is a
een constant getal.
Bij de drie voorbeelden hierboven horen de formules: S =
1200/k en R = a/O
en t = 40/s |
| |
|
|
|
Laten we dat
voorbeeld met die weerstand als rekenvoorbeeld gebruiken.
De elektrische weerstand (R) van een stroomdraad is omgekeerd
evenredig met de oppervlakte van de doorsnede (O)
van die draad. Bij een doorsneden van 4 mm2 hoort een
weerstand van 20
Ω (dat laatste rare tekentje is de eenheid van weerstand en
die spreek je uit als "Ohm").
Hoe groot is de weerstand bij een doorsneden van 2,8 mm2 ?
De formule is R = a/O
en dat geeft 20 = a/4 dus
a = 80 dus de formule is R = 80/O
O = 2,8 geeft dan R = 80/2,8
= 28,57
ΩHieronder zie je beide verbanden nog eens met de bijbehorende
grafiek. |
| |
|
|
|
|
 |
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
Maak een formule bij de volgende
problemen: |
| |
|
|
|
| |
a. |
Een auto rijdt 1 op 15. Dat wil zeggen
dat hij met 1 liter benzine 15 kilometer kan rijden.
1 liter benzine kost op dit moment 1,20.
Maak een formule voor het bedrag (B) dat je aan benzine kwijt bent bij een
afstand van a kilometer |
| |
|
|
|
| |
b. |
Als je een gewicht aan een veer hangt,
dan rekt hij uit. Hoe zwaarder het gewicht, des te verder rekt de
veer uit.
De uitrekking is recht evenredig met het gewicht.
Bij een gewicht van 20 kilogram rekt een bepaalde veer 4 cm uit
Geef een formule voor de uitrekking (U) van deze veer bij een
belasting B. |
| |
|
|
|
| |
c. |
Wetenschappers hebben tussen 1990 en
2000 het aantal hazen in het oostelijke deel van Schiermonnikoog
gemeten. Hazen doen het goed op Schiermonnikoog omdat er op het
eiland niet veel natuurlijke vijanden van de haas wonen. Het
aantal hazen in het zeshonderd hectare grote gebied schommelde
gedurende de onderzoeksperiode tussen de 320 en 596.
De leefruimte (L) per haas is de oppervlakte (in m2)
die een haas gemiddeld tot zijn beschikking heeft.
Geef een formule voor de leefruimte
per haas als functie van het aantal hazen (n) bij dit onderzoek. |
| |
|
|
|
| 2. |
Tussen twee
variabelen A en B bestaat een verband. We weten dat bij A = 24
hoort B = 7
We willen graag berekenen welke waarde van A hoort bij B = 12. |
| |
|
|
|
| |
a. |
Bereken die waarde
van A als A en B recht evenredig zijn |
| |
|
|
|
| |
b. |
Bereken die waarde
van A als A en B omgekeerd evenredig zijn. |
| |
|
|
|
| 3. |
examenvraagstuk HAVO
wiskunde A, 2015.
Geld lenen kost geld. Soms
kost het heel veel geld. Vooral als je direct een paar honderd euro
nodig hebt. In dit soort situaties kun je een flitslening nemen. Je
leent een niet al te groot geldbedrag en betaalt dit na een korte
periode terug.
Er bestaan verschillende websites waar je geld kunt lenen. Op de
website flitsmoney.nl staat dat er geen rente wordt berekend. Je
hoeft alleen behandelingskosten te betalen. Zie de volgende tabel. |
| |
|
|
|
| |
| te lenen bedrag (in euro) |
behandelingskosten (in euro) |
| 100,00 |
25,00 |
| 250,00 |
62,50 |
| 300,00 |
75,00 |
| 375,00 |
93,75 |
|
| |
|
|
|
| |
Als je bijvoorbeeld
100,00 wilt lenen, krijg je dit geld binnen 10 minuten op je
bankrekening. Dit bedrag moet samen met de 25,00
behandelingskosten na 30 dagen worden terugbetaald.
Er is bij Flitsmoney een (recht) evenredig verband tussen het totaal
terug te betalen bedrag en het te lenen bedrag.
Laat dit met
berekeningen zien. Controleer hiervoor alle waarden in de tabel.
|
| |
|
|
|
| 4. |
De "4 mijl van Groningen" is
een jaarlijks terugkerend evenement waarbij duizenden deelnemers
een afstand van 4 mijl (6437 meter) hardlopen. Chris is één
van deze lopers. Hij heeft de 4 mijl in 2006 gelopen in 28
minuten en 15 seconden en in 2007 deed hij er 27 minuten en 50
seconden over.
Hij berekent dat zijn gemiddelde snelheid in die twee jaren
gelijk was aan 13,67 en 13,88 km/uur. |
| |
|
|
|
| |
a. |
Controleer die berekeningen. |
|
| |
|
|
| |
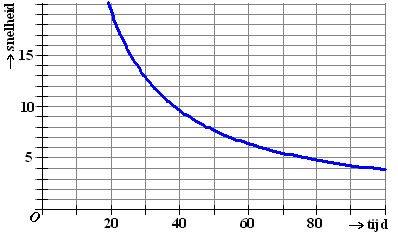
Hiernaast staat een
grafiek met voor elke gelopen tijd (in minuten) de bijbehorende
snelheid (in km/uur). |
| |
|
|
| |
b. |
Geef een formule voor die grafiek en
bereken daarmee welke tijd Chris moet lopen om een gemiddelde
van 15 km/uur te halen. |
| |
|
|
|
| |
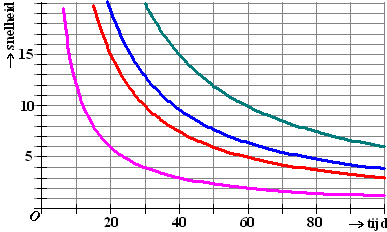
Chris is steeds meer en
meer lange-afstandslopen gaan doen. Voor zijn trainingen heeft
hij voor een aantal afstanden een grafiek als hierboven gemaakt.
Die grafieken zie je in de figuur hiernaast. |
|
| |
|
|
| |
c. |
Geef voor elk van die grafieken een
formule en leg uit bij welke gelopen afstand de betreffende
grafiek hoort. |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|