© h.hofstede (h.hofstede@hogeland.nl)

 
Breuken in breuken.
1.  Delen door een breuk.  
Laten we een getal x gaan delen door 2/5. Gewoon voor de gein....
Nou is een  leuke eigenschap van 2/5 dat, als je het met 5/2 vermenigvuldigt, er precies 1 uitkomt:  5/2 • 2/5 = 1
Dat kunnen we handig gebruiken: vermenigvuldig beide kanten van deze laatste vergelijking met x.
Dat geeft  x •  5/2 • 2/5 = x
Maar kijk hiernaast wat er gebeurt als je beide kanten door 2/5 deelt, zoals volgens onze balansmethode mag.
Dan blijkt te gelden dat  x gedeeld door 2/5 hetzelfde is als x maal 5/2.
En wat voor 2/5 geldt, geldt natuurlijk precies zo voor 3/7 en 4/11 en .....

Conclusie in woorden:

delen door een breuk = vermenigvuldigen met het omgekeerde

Conclusie in letters:

Je kunt het natuurlijk ook in één keer zien door teller en noemer van de linkerkant beiden met c te vermenigvuldigen. Dan valt de c  weg uit de noemer en komt er in de teller ac te staan.

Het kan natuurlijk ook in deze variant:
 
 
 
Haal deze en de vorige niet door elkaar!!!!
   
voorbeeld 1.
 
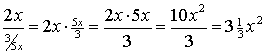voorbeeld 2.
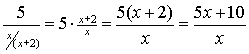2.  Overal breuken!
Gebruik het eenvoudige principe dat je de teller en de noemer van een breuk mag vermenigvuldigen met hetzelfde getal. Dan blijft de breuk gelijk. Deze eigenschap kun je gebruiken om de noemers van ongewenste breuken weg te werken.
Hier is een voorbeeld van hoe dat in z'n werk gaat:

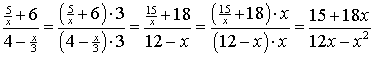
Bij de eerste stap is het doel om de  x/3 in de noemer weg te halen. Daarom zijn de teller en de noemer beiden met 3 vermenigvuldigd. Zoals je ziet verdwijnt de breuk x/3 daardoor.
Bij de derde stap willen we ook de breuk 15/x weghalen. Dat doen we door teller en noemer beiden met x te vermenigvuldigen. Het resultaat is een breuk zonder daar nog weer breuken in. Deze laatste ziet er vrij "normaal" uit.
 
 
 
OPGAVEN
1. Schrijf de breuken zó, dat er in teller en noemer geen breuken meer staan.
a. e.
b. f.
c. g.
d. h.
2. Gegeven zijn de volgende twee vergelijkingen:

             
  Maak hier van een vergelijking van de vorm:

   
  Waarin  a, b, c en d  constante getallen zijn.
 
3. Bij de helpdesk van een bedrijf werken twee medewerkers.
De eerste medewerker gebruikt gemiddeld 2,5 minuten om een telefoontje af te handelen.
De tweede medewerker gebruikt gemiddeld m minuten om een telefoontje af te handelen.
Voor het gemiddeld aantal minuten per telefoontje (G)  van beide medewerkers samen geldt dan de volgende formule:
 

  a. Toon aan dat deze formule klopt.  
       
  b. Bereken de benodigde m om een gemiddelde van 2 min/telefoontje te halen.
       
  c. Herleid de formule voor G tot een zo eenvoudig mogelijke breuk.
       
4. Welke breuk is de grootste?
Laat dat zien zonder je GR te gebruiken.
       
 

       

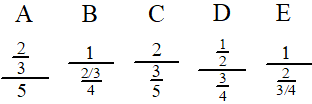© h.hofstede (h.hofstede@hogeland.nl)