| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
ax + by = c |
 |
Je kent natuurlijk
nog wel de formule van een rechte lijn: y = ax +
b. We noemden dat een lineair verband.
Maar er zijn meer manieren om zo'n lineair verband weer te geven.
De formule 2x + 5y = 10 geeft namelijk σσk een lineair
verband.
Dat kun je makkelijk zien door de formule om te gaan schrijven:
2x + 5y = 10
5y = 10 - 2x
y = 2 - 0,4x
Daar zie je al de basisformule van een rechte lijn y = ax
+ b met beginpunt b = 2 en helling a
= -0,4. Die kun je dan makkelijk tekenen, zie de figuur linksonder.
Maar je kunt hem nog veel makkelijker tekenen!
Neem in 2x + 5y = 10 gewoon x = 0
dan vind je y = 2. En neem daarna y = 0
dan vind je x = 5.
Teken gewoon de twee punten (0, 2) en (5, 0). Geodriehoek erlangs en
hup! Daar is de lijn al. Zie de figuur rechtsonder. |
| |
|
|
|
|
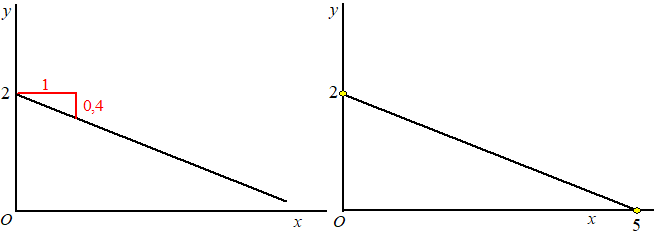 |
| |
|
|
|
Formules zelf opstellen.
Die vorm ax + by = c kom je vaak tegen als je
zelf een formule bij een gegeven verhaaltje probeert op te stellen.
Dat kan ik het best laten zien aan de hand van een voorbeeld.
Voorbeeld.
Stel dat ik in de winkel een aantal flessen wijn van elk 6,00 koop en
ook een aantal flessen likeur van elk 15,00.
Maak een formule als ik in totaal 120,- moet betalen.
Nou, stel dat ik W flessen wijn koop, dan kosten die samen
6 W euro.
En als ik L flessen likeur koop dan kosten die samen 15
L euro.
Mijn hele bestelling kost dan 6W + 15L euro.
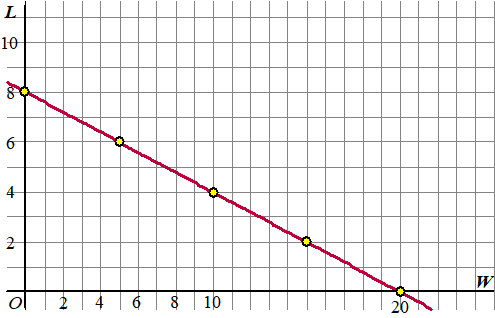
Dus kan ik de vergelijking 6W + 15L = 120 opstellen.
En dat geeft de rechte lijn hieronder (ik heb ervoor gekozen om L
op de -as te zetten en W op de x-as maar dat had
natuurlijk net zo goed andersom gekund). |
| |
|
|
|
|
 |
| |
|
|
|
Een slimmerik zal nog
opmerken dat het aantal flessen natuurlijk een geheel getal moet zijn
zodat eigenlijk alleen de roosterpunten van die lijn mogelijk zijn.
Het voorbeeld uitgebreid.
Stel dat we verder weten dat ik in totaal 17 flessen heb gekocht.
Dan zou dat van de getekende gele stippen hierboven als enige
mogelijkheid het punt (15, 2) geven, dus dan heb ik 15 flessen
wijn en 2 flessen likeur gekocht.
In plaats van dat af te lezen kunnen we dat natuurlijk ook berekenen!
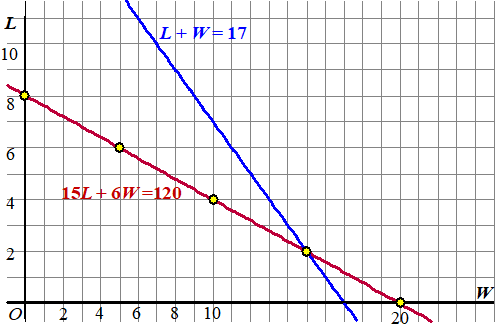
Als er in totaal 17 flessen zijn gekocht dan geeft dat de tweede
vergelijking L + W = 17 en dat is weer een rechte
lijn.
Laten we die erbij in tekenen: |
| |
|
|
|
|
 |
| |
|
|
|
(15, 2) is inderdaad
het snijpunt van beide lijnen.
Maart dat snijpunt kunnen we natuurlijk ook wiskundig berekenen in
plaats van af te lezen:
Dat gaat zσ:
15L + 6W = 120
15L = 120 - 6W
L = 8 - 0,4W
L + W = 17
L = 17 - W
En nu hebben we twee lijnen waarvan we het snijpunt kunnen berekenen.
Dat kan uiteraard met de optie intersect van de GR(Y1 = 8
- 0,4X en Y2 = 17
- X) maar het kan ook met algebra door
de formules achter elkaar te schrijven:
8 - 0,4W = 17 -
W
0,6W = 9
W = 15 en dan is L = 17 -
15 = 2 dus inderdaad 15 flessen wijn en 2 flessen likeur.
Van Nederlands naar Wiskunde...
Om zelf formules te maken moet je meestal sommige hoeveelheden
gelijkstellen aan x of aan y (zoals de L en
W hierboven), maar daarna moet je ook nog die Nederlandse
tekst zien te vertalen naar een wiskundige formule.
Hier zijn een aantal voorbeelden van hoe dat gaat: |
| |
|
|
|
| Nederlandse tekst |
Wiskundige formule |
"x is vijf
groter dan y"
"er zijn tweemaal zoveel y als x"
"het verschil tussen x en y is 18"
"de helft van x is twee minder dan y" |
x = y + 5
y = 2x
x - y = 18 of y
- x =
18
0,5x = y - 2 |
|
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
Voor het huren van een auto
betaal ik een vast bedrag per uur en verder een vast bedrag per gereden kilometer.
Als ik een auto 12 uur huur en er 500 km mee rijd, dan moet ik 214,40
betalen
Als ik een auto
8 uur huur en er 300 km mee rijd, dan moet ik 129,60 betalen.
Noem de uurprijs
U
en de
kilometerprijs K. |
| |
|
|
|
| |
a. |
Stel een formule op
die volgt uit het bedrag 214,40, en ook een formule
die volgt uit het bedrag 129,60 |
| |
|
|
|
| |
b. |
Teken de grafieken
van beide formules en bereken het snijpunt ervan. |
| |
|
|
|
| 2. |
In een slagroompunt zit 120 gram
suiker en in een moorkop zit 80 gram suiker. Een slagroompunt kost
2,- en een moorkop kost
2,50.
Ik koop bij de banketbakker voor 156,
- aan slagroompunten en moorkoppen, en ik heb dan in totaal 7120 gram suiker
gekocht.
Stel dat ik S slagroompunten en M moorkoppen
kocht. |
| |
|
|
|
| |
a. |
Stel een formule op
voor de hoeveelheid suiker, en ook een formule voor de kosten van de
bestelling. |
| |
|
|
|
| |
b. |
Bereken hoeveel ik
van elk kocht. |
| |
|
|
|
| 3. |
In een vaas zitten
rode en blauwe knikkers.
Het aantal rode knikkers is 5 kleiner dan de helft van het aantal
blauwen.
Er zijn 12 meer blauwe dan rode knikkers.
Hoeveel knikkers zitten er in totaal in de vaas? |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|