Hydrostatische druk.
Als je een voorwerp onder water houdt, dan wordt er door het water een opwaartse kracht op uitgeoefend, door de druk van het water. Die waterdruk heet de hydrostatische druk, en wordt gegeven door de formule  P = r • g • d Daarin is P de druk, r de dichtheid van het water, d de afstand (in meter) onder water, en g de gravitatieversnelling. Voor de rest van deze les nemen we aan dat g = 9,81 m/s2 en r = 1000 kg/m3 Dan verandert bovenstaande formule in P = 9810 • d. Voor de kracht op een oppervlakte geldt dan  F = P • A  waarin A de grootte van het oppervlak (in m2) is, en F de kracht in Newton (N) Deze formule werkt prima voor een horizontale plaat onder water.
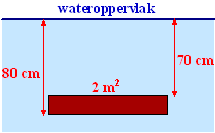
Neem aan dat je een plaat met oppervlakte 2 m2 en dikte 10 cm horizontaal onder water houdt, waarbij de onderkant van de plaat 80 cm onder het wateroppervlak zit. Op de onderkant werkt dan een kracht F = 9810 • 0,80 • 2 = 15696 N omhoog en op de bovenkant werkt een kracht F = 9810 • 0,70 • 2 = 13734 N omlaag. Dus er werkt een netto kracht 1962 N opwaarts.
Even een beroemd tussendoortje: De inhoud van de plaat is  2 • 0,10 = 0,2 m3, en 0,2 m3 water heeft massa 100 • 0,2 = 200 kg dus daarop werkt een kracht F = 200 • 9,81 = 1962 N. Goh... Grappig....De opwaartse kracht is gelijk aan het gewicht van de verplaatste hoeveelheid water.
Maar als zo'n oppervlak niet overal even breed is, is de hydrostatische druk ook niet overal gelijk. Je moet zo'n totale kracht F dan opgebouwd zien uit allemaal kleine stukjes dF. JUIST! Daar komt een integraal aan te pas. Voorbeeld 1.
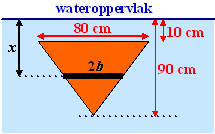
Een driehoekige plaat met constante dikte D = 1 wordt onder water gehouden. De afmetingen in het vooraanzicht zijn als hiernaast. In deze plaat is op diepte x een strookje met hoogte dx en breedte 2b getekend. Kies dx zo klein mogelijk, dan is het strookje bij benadering een rechthoek. Op de bovenkant van zo'n strookje werkt een kracht omlaag van 9810xA Op de onderkant werkt een kracht omhoog van  9810(x + dx)A Netto geeft dat een kracht omhoog van 9810 • dx • A   Voor dat strookje geldt:  dF = 9810 • (2bDdx) = 19620 • b • dx  (D = 1) Uit gelijkvormige driehoeken volgt  40/80 = b/(90 - x) dus b = 45 - 0,5x Dan is dF = 19620 • (45 - 0,5x) • dx Voor de totale kracht moet je de integraal van x = 0,1 tot x = 0,9 nemen:
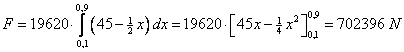