|
|||||||||||||||||||||
 |
|||||||||||||||||||||
| ExponentiŽle formule opstellen uit twee punten. | |||||||||||||||||||||
| In een
vroegere les
hebben we ooit behandeld hoe je door twee willekeurige punten de formule
van een lineair verband kunt opstellen. Nou, laten we dat voor een exponentieel verband dan ook maar doen...... Stel bijvoorbeeld dat je op ťťn of andere manier hebt ontdekt dat een exponentieel verband door (4, 8) en (7, 12) gaat. De formule zal altijd zijn y = B ◊ gx Je zult moeten vinden welke g en welke B bij dit verband horen. Stap 1. Dan gaan we eerst op zoek naar de groeifactor g. We zien aan de twee punten: in 3 stappen (7 - 4) is de groeifactor 12/8 = 1,5 Dat betekent dat g3 = 1,5 dus g = (1,5)1/3 = 1,145 (we werken in drie decimalen nauwkeurig) De tussenstand is voorlopig de formule y = B ◊ 1,145x Stap 2. Hoe vinden we B? Simpel: vul gewoon ťťn van beide punten in!!! Neem bijvoorbeeld het punt (4, 8). Dat betekent x = 4 en y = 8 dus 8 = B ē 1,1454 ⇒ 8 = B ◊ 1,72 ⇒ B = 8/1,72 = 4,65 De vergelijking is dan: y = 4,65 ◊ 1,145x |
|||||||||||||||||||||
|
|
|||||||||||||||||||||
| OPGAVEN. | |||||||||||||||||||||
| 1. | a. | De grafiek van een
exponentieel verband gaat door de punten (2, 12) en (14, 50) Geef een formule. |
|||||||||||||||||||
| b. | De grafiek van een
exponentieel verband gaat door de punten (5, 130) en (9, 60) Geef een formule. |
||||||||||||||||||||
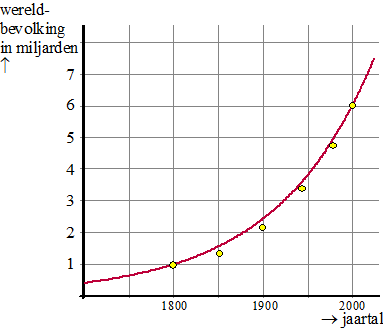
| 2. | Vanaf 1700 tot nu is
de wereldbevolking erg snel gegroeid. In de grafiek hiernaast vind je voor een aantal jaartallen de grootte van de wereldbevolking op dat moment (in miljarden mensen) Het valt hen op dat het gewicht in deze periode bijna exponentieel verloopt. De exponentiŽle rode grafiek hiernaast past redelijk goed bij de gevonden meetwaarden. Daarin is t = 0 in 1700 genomen. Het lijkt erop dat die grafiek precies door het eerste en laatste meetpunt gaat. In 1800 was de wereldbevolking ongeveer 0,95 miljard en in 2000 was de wereldbevolking ongeveer 6,0 miljard. Stel een formule op van de exponentiŽle grafiek die precies door deze twee meetpunten gaat. |
|
|||||||||||||||||||
| 3. | De Hindenburg was een
enorm Duits luchtschip dat in de jaren 1936/1937 trans-Atlantische
vluchten ondernam. Het schip was via zestien enorme gascellen gevuld met
een enorme hoeveelheid waterstof. Een vlucht van Franfurt am Main (D) naar Lakehurst, New Jersey (USA) duurde zo'n zestig uur. Ondanks de zorgvuldige constructie is het niet te voorkomen dat zo'n enorm schip toch wat waterstof lekt. De volgende tabel geeft aan hoeveel waterstof er na t uur vliegen nog aanwezig is inde Hindenburg. |
|
|||||||||||||||||||
|
|||||||||||||||||||||
| a. | Leg duidelijk uit hoe uit
bovenstaande tabel valt af te leiden dat het hier om een
exponentieel verband gaat Stel een formule op voor de hoeveelheid waterstof in de Hindenburg als functie van de tijd in uren met t = 0 op het moment van vertrek (als de Hindenburg helemaal gevuld is). |
||||||||||||||||||||
| Om veilig te kunnen blijven vliegen is minimaal 120000 liter waterstof benodigd. | |||||||||||||||||||||
| b. | Bereken met de in vraag a) opgestelde formule hoe lang een vlucht met de Hindenburg maximaal kon duren. | ||||||||||||||||||||
| 4. | Examenvraagstuk
VWO wiskunde A, 2016-I Gemiddeld duurt een zwangerschap bij de mens 38 weken. Een ongeboren kind van 8 weken of ouder wordt een foetus genoemd. In de volgende tabel staat het (gemiddelde) lichaamsgewicht G in gram van een foetus bij een leeftijd van t weken. |
||||||||||||||||||||
|
|||||||||||||||||||||
|
In deze opgave willen we onderzoeken welk model er
bij deze tabel zou kunnen passen. G = b ē at met a en b constanten.Veronderstel dat de groei tussen week 8 en week 10 inderdaad exponentieel verloopt. |
|||||||||||||||||||||
| a. | Bereken dan de constanten a en b. | ||||||||||||||||||||
| ExponentiŽle groei is echter geen goed model voor de groei van de foetus in de gehele periode van 8 tot 38 weken. Dit kun je afleiden uit de tabel. | |||||||||||||||||||||
| b. | Laat dat met een berekening zien. | ||||||||||||||||||||
|
|
|||||||||||||||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||||||||||||||