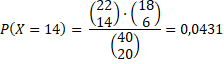|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fisher toets. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De Fishertoets
(genoemd naar de statisticus Ronald Fisher) is een toets die wordt
gebruikt bij kruistabellen. In praktijk vooral bij kruistabellen van geringe omvang, omdat voor grotere kruistabellen een χ2- toets handiger is (maar die is bij kleine tabellen te onnauwkeurig). Fisher's toets is eigenlijk altijd beter (die is namelijk exact, en niet afhankelijk van een benadering zoals de χ2 toets wel is), maar het is af en toe wel vrij veel werk, zoals je hieronder kunt zien. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Als je een kopje thee
met melk drinkt, doe je dan eerst de melk erin, en daarna de thee?
Of andersom? Als je denkt "wat maakt het in vredesnaam uit?" dan
heb je het helaas verkeerd! Daar kwam dr. Ronald Fisher wel
achter........ Hij was één van een groep academici die in 1920 in Rothemsted (Engeland) om 4 uur 's middags thee ging drinken. Zich van geen kwaad bewust gaf hij een collega, Dr. Blanche Muriel, een kopje thee. Maar zij weigerde, omdat hij eerst de thee in het kopje had gedaan en daarna pas de melk! Getver!! Fisher lachte haar uit en zei dat zij dat met geen mogelijkheid kon proeven, maar ze hield voet bij stuk. Als echte academici ontwierpen ze natuurlijk een experiment om de bewering van Muriel te testen. Fisher gaf haar 8 koppen thee te proeven. Vier waarbij eerst de melk erin was gedaan, en vier met eerst de thee. Zij moest ze in een "melk-eerst-groep en een "thee-eerst-groep" sorteren, en ze moest ze allemaal goed hebben! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Waarom allemaal? Is
dat niet wat streng? Laten we eens kijken hoeveel manieren er mogelijk zijn als je zomaar wat in twee groepen van 4 sorteert. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
• |
allemaal goed kan maar op één manier | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
• |
allemaal fout kan ook maar op één manier | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| • | één paar fout kan op
16 manieren. Stel dat zij de kopjes aangeboden krijgt in de volgorde MMMMTTTT (M = melk eerst, T = thee eerst) Dan zijn er 4 mogelijkheden om de kiezen welke M er fout gaat, en bij elk van die 4 mogelijkheden weer 4 mogelijkheden om daarna de T fout te doen. In totaal 16 mogelijkheden. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| • | één paar goed kan, volgens dezelfde redenatie, ook op 16 manieren. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
• |
Twee paar goed: welke twee M goed zijn kan op 4 nCr 2 = 6 manieren, welke twee T daarna ook op 6 manieren, dus in totaal op 36 manieren. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In totaal zijn er 1 +
1 + 16 + 16 + 36 = 70 mogelijke uitkomsten. Allemaal goed heeft een kans van 1/70 = 0,014 Eén fout heeft een kans van 16/70 = 0,228, dus als je een resultaat van minstens 3 paar goed nog zou accepteren dan is de overschrijdingskans 24,2% en dat is natuurlijk veel te groot voor zo'n serieus academisch experiment. Het verhaal gaat overigens dat Blanche Muriel ze allemaal goed had...... Deze kruistabel hoort bij dit beroemde thee-experiment: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Maar die totalen in
het grijze gebied liggen al vast!! Muriel zal immers zorgen dat die
allemaal op 4 uitkomen. Dus één van de vier vraagtekens bepaalt meteen de hele tabel. Als bijvoorbeeld het rode vraagteken bekend is, is de rest ook bekend. Fisher ontdekte dat zo'n vraagteken in de tabel een hypergeometrische verdeling volgt. Het aantal manieren waarop het vraagteken linksboven bijvoorbeeld gelijk is aan 3 is (4 nCr 3) • (4 nCr 1) = 16 zoals we hierboven al zagen. Dus de kans is 16/70 (die 70 is natuurlijk 8 nCr 4). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Voorbeeld. Men verricht een onderzoek naar het wel of niet in het bezit zijn van een spelcomputer onder 20 jongens en 20 meisjes. Dat gaf de volgende resultaten: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Mogen we concluderen
dat meer jongens dan meisjes een spelcomputer hebben (neem
α = 0,05, eenzijdig)? H0 = "Er is geen verschil" We vragen ons dus nu af: Hoe groot is de kans dat van 20 jongens en 20 meisjes, waarvan er 22 een spelcomputer hebben, minstens 14 jongens bij die 22 zijn? Stel het aantal jongens X. Het is alsof je uit een vaas hebt met 40 knikkers: 22 met-een-computer en 18 zonder-computer . Je moet er 20 uithalen om de eigenschap "jongen " aan te geven. Wat is de kans dat je dan van de 22 met-computer-knikkers er 14 kiest en van de 18 zonder-computer-knikkers 6? 14 kiezen uit de 22 kan op 22 nCr 14 manieren, en daarna nog 6 kiezen uit de 18 kan op 18 nCr 6 manieren. Samen geeft dat voor de kans om precies 14 jongens te kiezen: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Voor de
overschrijdingskans "minstens 14 jongens" moeten we ook de
grotere aantallen meenemen: P(X = 15) = .... = 0,0106 P(X = 16) = .... = 0,0017 P(X = 17) = .... = 0,0002 P(X = 18) = .... = 0,0000 P(X = 19) = .... = 0,0000 P(X = 20) = .... = 0,0000 De totale overschrijdingskans is 0,0556 en dat is groter dan 0,05 dus we mogen NIET aannemen dat er meer jongens dan meisjes een spelcomputer hebben. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Als er meer dan twee categorieën zijn, dan kun je deze Fisher toets niet gebruiken, maar er is wel een uitbreiding voor: de Fisher-Freeman-Halton toets. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||