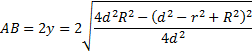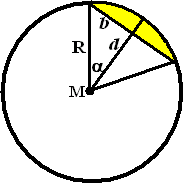|
|||||||||||||||||||||
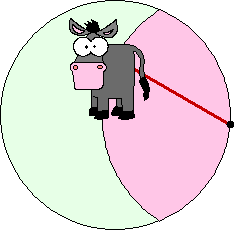
| De grazende ezel. | |||||||||||||||||||||
|
|
|||||||||||||||||||||
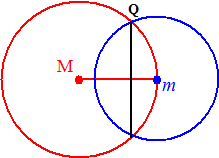
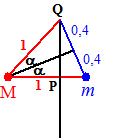
| Een ezels zit vast
aan een touw. Daardoor kan hij slechts op een deel van de weide waarop
hij zich bevindt
grazen. De ezel bevindt zich op een cirkelvormige weide met straal 1, en zit ergens aan het hek aan de binnenkant vast aan een touw met lengte 0,8. Hoeveel weiland kan de ezel afgrazen? |
|||||||||||||||||||||
| Ach, kom, weet je
wat? ...... Laten we meteen maar het algemenere geval bekijken:
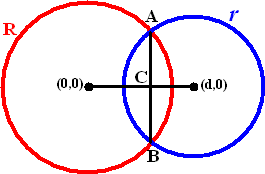
Twee cirkels met stralen R en r en middelpunten (0,0) en (d,0) snijden elkaar. Hoe groot is de gemeenschappelijke oppervlakte? Eerst gaan we proberen lengte AB te vinden: De vergelijkingen van de cirkels zijn: |
|
||||||||||||||||||||
| Snijden geeft:
(x- d)2 + (R2 - x2)
= r2 ⇒ x2
- 2dx + d2 - x2 = r2
- R2 x oplossen en weer invullen in y2 = R2 - x2 geeft: |
|||||||||||||||||||||
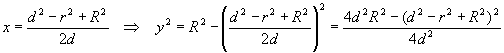 |
|||||||||||||||||||||
| Lengte AB is gelijk aan 2y: | |||||||||||||||||||||
|
|
|||||||||||||||||||||
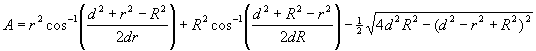 |
|||||||||||||||||||||
|
|||||||||||||||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||||||||||||||