| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Dubbelintegralen. |
| |
|
|
|
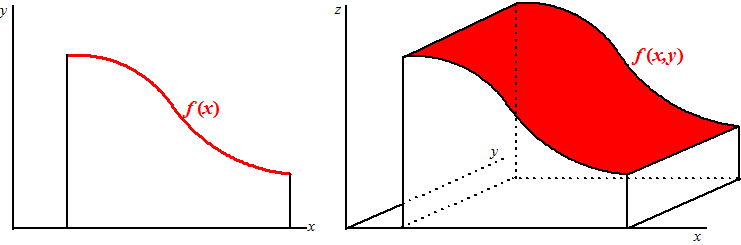
Een gewone integraal
die hebben we ooit leren kennen als de oppervlakte onder een grafiek
f(x) , en die berekenden we door allemaal
rechthoekjes van breedte dx en hoogte f(x) te maken
en de oppervlakten daarvan op te tellen (een Riemann-som, weet je nog?)
Deze les gaan we de ruimte in!
We bekijken het driedimensionale geval van een integraal.
Er is nu een tweedimensionale functie f(x, y)
een daarvan willen we de inhoud boven een gebied in het xy-vlak
berekenen. Zie de figuur rechtsonder. (de rand naar achteren is
ongeveer recht getekend voor de eenvoud, maar kan natuurlijk elke vorm hebben) |
| |
|
|
|
|
 |
| |
|
|
|
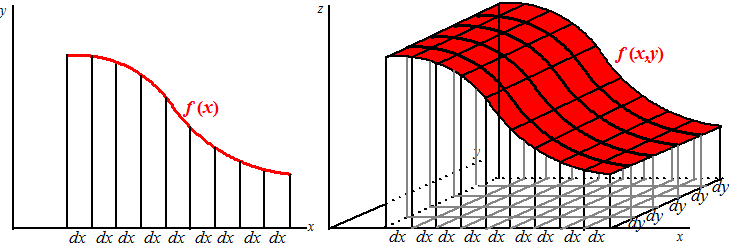
| De tweedimensionale
oppervlakte berekenden we door het vlakdeel in rechthoekjes te verdelen,
dus op dezelfde manier gaan we nu de driedimensionale inhoud in staafjes
verdelen: |
| |
|
|
|
|
 |
| |
|
|
|
In de figuur rechts
moeten we dus van elk staafje de inhoud uitrekenen en dan al die
inhouden optellen. Als de staafjes maar dun genoeg zijn (dx en dy
zo klein mogelijk) dan zijn het bij benadering balken, en dan is de
inhoud dx • dy • f(x, y)
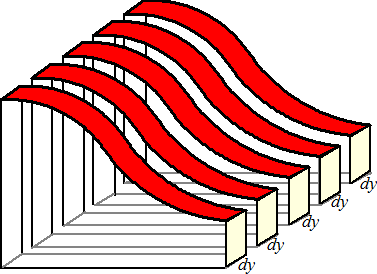
Voor de totale inhoud moeten we nu weer sommeren, maar ja, wel sommeren
over alle dx én over alle dy
Dat zou zó kunnen: |
| |
|
|
|
|
 |
| |
|
|
|
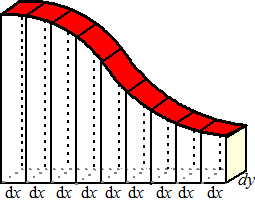
De inhoud van één
zo'n deel (met dikte dy) kun je nu uitrekenen door alle dx
daarvan te sommeren.
Voor de inhoud van dit ene deel geldt dan: |
 |
| |
|
|
|
| |
|
| En als je dx
maar klein genoeg neemt dan wordt dat een integraal: |
| |
|
|
|
| |
|
|
|
Merk nog even op dat
die integraal de oppervlakte van de voorkant is (en ook de achterkant
als dy maar klein genoeg is).
Als je dit ene deel hebt uitgerekend moet je daarna natuurlijk nog al
die dy-delen bij elkaar optellen. Dat wordt (als je nu dy maar
klein genoeg kiest) wéér een som: |
|
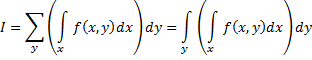 |
| |
|
|
|
| Maar ja, je zou
natuurlijk ook net zo goed de inhoud van die hele figuur eerst in
allemaal stukken met breedte dx kunnen verdelen: |
| |
|
|
|
|
 |
| |
|
|
|
| En dan moet je één
zo'n deel (met vaste x) weer uitrekenen met een som over alle dy.
Dat wordt dan de oppervlakte van de zijkant. Dat geeft: |
| |
|
|
|
|
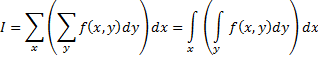 |
| |
|
|
|
| Die beide manieren
geven dezelfde oplossing (namelijk de totale inhoud). Daarom schrijven
we dat voortaan als één integraal; een zogenaamde dubbelintegraal: |
| |
|
|
|
|
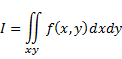 |
| |
|
|
|
Bedenk goed dat je
zelf mag kiezen in welke volgorde je de integralen uitrekent!
•
OF je neemt eerst x als constante en berekent de integraal van dy,
en daarna integreer je dat resultaat nog eens over dx
•
OF je neemt eerst y als constante en berekent de
integraal van dx, en daarna integreer je dat resultaat nog eens
over dy |
| |
|
|
|
Voorbeeld.
Bereken de dubbelintegraal van de functie f(x,
y) = x2y over het gebied
0 ≤ x ≤ 4
en 2 ≤ y ≤
6.
Doe dat op twee verschillende manieren. |
| |
|
|
|
Oplossing.
eerst integreren over x: |
|
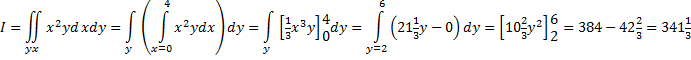 |
| |
|
|
|
| eerst integreren over
y: |
|
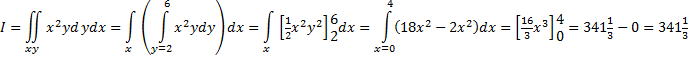 |
| |
|
|
|
| Gelukkig maar.... dat
is hetzelfde! |
| |
|
|
|
|
Een Riemann- Middensom |
| |
|
|
|
Op precies dezelfde manier waarop
we de oppervlakte onder een grafiek konden benaderen met een
Riemann-Middensom kunnen we nu de inhoud onder een vlakdeel benaderen
met zo'n Riemann-Middensom.
Ter illustratie maar weer een enkele en een dubbele integraal naast
elkaar, zodat je goed de overeenkomsten kunt zien.
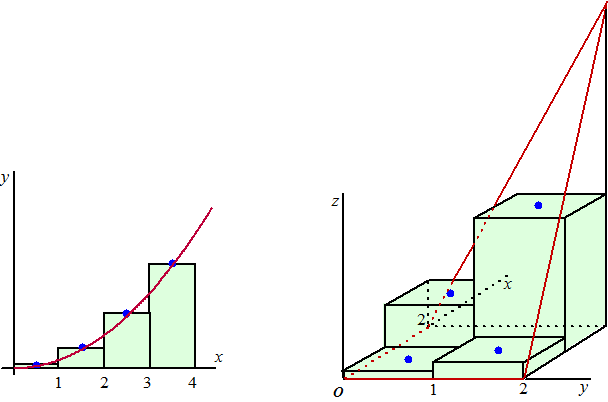
• Links willen we de oppervlakte onder de grafiek van f(x)
= x2 van x = 0 tot x = 4 berekenen
• Rechts willen we de inhoud onder het vlakdeel van de functie g(x,
y) = x2y voor x en y
tussen 0 en 2 berekenen. |
| |
|
|
|
|
 |
| |
|
|
|
| • |
Links berekenen we de
functiewaarde in de vier blauwe stippen
f(0,5) = 0,25 en f(1,5) = 2,25 en f(2,5)
= 6,25 en f(3,5) = 12,25
Voor de oppervlaktes van die rechthoekjes vermenigvuldig je met
Δx = 1, en dan tel de die rechthoekjes
op
Dat geeft als benadering oppervlakte 0,25 • 1 + 2,25 • 1 +
6,25 • 1 + 12,25 • 1 = 21 cm2 |
| |
|
|
|
| • |
Rechts bereken je de hoogte van
die vier blauwe stippen
(er zweeft daar nog een rood vlak boven dat precies door die vier
stippen gaat, maar dat tekent wat lastig)
g(0.5, 0.5) = 0,125 en g(1.5, 0.5) = 1,125
en g(0.5, 1.5) = 0,375 en g(1.5, 1.5) =
3,375
Voor de inhoud van die balkjes vermenigvuldig je die hoogtes met
ΔxΔx
= 1 • 1 = 1 en dan tel je die inhouden op.
Dat geeft als benadering voor de inhoud 0,125 • 12 +
1,125 • 12 + 0,375 • 12 + 3,375 • 12 =
5 cm3 |
| |
|
|
|
|
Het blijft natuurlijk wél een inhoud
hé? |
| |
|
|
|
| Soms helpt het best veel om je te
blijven bedenken dat het wel om een inhoud gaat. Neem de volgende zeer
lastige dubbelintegraal: |
|
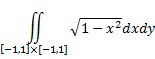 |
Het integratiegebied is dus het
vierkant voor x en y tussen -1 en 1.
Tja, naar x integreren is nogal lastig. Wat is de
primitieve van f(x) = √(1
- x2)??
Oké, dat blijkt gelijk te zijn aan F(x) =
1/2
• (x√(1 - x2)
+ arcsinx).
Controleer maar door te differentiëren!!! Tja, je moet
er maar opkomen......
|
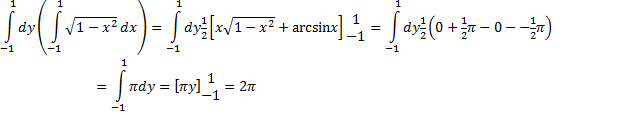 |
| |
|
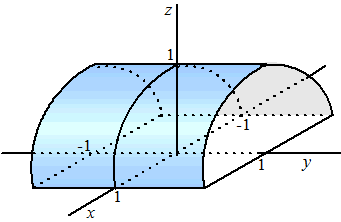 |
Maar het wordt allemaal een stuk
makkelijker als je je realiseert dat de functie z =
√(1 - x2)
een stuk van een cilindermantel is!
Zie de figuur hiernaast.
Met die integraal wordt dus eigenlijk gevraagd de inhoud onder die
cilindermantel. Dat is een halve cilinder met r = 1 en h =
2.
Dat is een halve cilinder en die heeft inhoud
1/2
•
π • 12 • 2 = 2π
Voilá!!!! |
| |
|
|
|
Een paar eigenschappen samengevat.
- die we trouwens stiekem eigenlijk al gebruikt hebben-
Hier staan nog even op een rijtje een paar eigenschappen van
dubbelintegralen die volgen uit de definities en figuren hierboven. Ik
hoop dat je ze logisch vindt...... |
| |
|
|
|
|
|
| |
|
|
|
| 1. |
Bereken de volgende integralen op twee manieren. |
| |
|
|
|
| |
a. |
De integraal van f(x,
y) = 2x + y over het gebied
1 ≤ x ≤
3 en 2 ≤ y
≤ 6 |
| |
|
|
|
| |
b |
De integraal van
f(x, y) = y√x
over het gebied 0 ≤
x ≤ 4 en 2
≤ y ≤ 4 |
| |
|
|
|
| |
c. |
De integraal van
f(x) = x2 + y over
het gebied 0 ≤ x
≤ 6 en 0
≤ y ≤
2 |
| |
|
|
|
| 2. |
Bereken de
volgende integralen op de manier die je maar wilt.
(De integratiegebieden zijn steeds aangegeven als [x1,
x2] × [y1,
y2] ) |
| |
|
|
|
| |
a. |
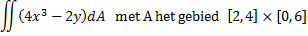 |
| |
|
|
|
| |
b. |
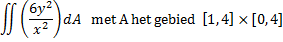 |
| |
|
|
|
| 3. |
Neem bij de volgende
twee integralen even de tijd om te beslissen naar welke
variabele je eerst integreert: |
| |
|
|
|
| |
a. |
 |
| |
|
|
|
| |
b. |
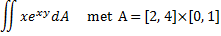 |
| |
|
|
|
| |
|
|
|
|
Soms kun je 't nog wat
versimpelen
(maar niet vaak....) |
| |
|
|
|
Die integrand is steeds
een functie f (x, y) van x en
van y. Heel soms komt het voor dat je die functie
f kunt schrijven als twee factoren waarvan de ene
alleen van x afhangt en de andere alleen van y.
Zó dus: |
|
|
| |
|
|
|
| Als dat kan, dan kun je
die dubbelintegraal ook meteen weer veranderen in twee enkele
integralen: |
| |
|
|
|
|
|
| |
|
|
|
| Ik hoop dat je dat
logisch vindt. Als je bijvoorbeeld eerst naar y besluit
te integreren, dan is dat stuk g(x) een constante
die je ook wel helemaal voor de y-integraal mag zetten.
En bij het daarna naar x integreren is dat y stuk
weer gewoon een constante. |
| |
|
|
|
| 4. |
Van de
integralen uit de opgaven 1 tm 3 kun je er twee op deze
simpelere manier berekenen.
Doe dat.... |
| |
|
|
|
| |
|
|
 |
|
| |
|
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|