depth first search

© h.hofstede (h.hofstede@hogeland.nl)

Grafen doorzoeken.

Als je een grote graaf wilt doorzoeken (op zoek naar een knooppunt of verbindingslijn met een bepaalde eigenschap) dan is het wel handig als je dat op een systematische en efficiënte manier kunt doen. Dat gaat uiteindelijk toch vaak met een computer, dus het is wel handig om een soort zoek-algoritme te hebben.

Nou zijn er daarvoor twee soorten op de markt: Diepte-eerst (Depth-First-Search; DFS) en Breedte-eerst (Breadth-First Search; BFS).De Engelse benamingen zijn zo algemeen dat ik ze overneem, en het zal hebben over DFS- en BFS-Search.

We nemen aan dat de grafen die we onderzoeken samenhangend zijn (als dat niet zo is moeten we de afzonderlijke componenten apart onderzoeken) en geen lussen hebben (als die er wel zijn laten we ze gewoon weg!).

Depth-First-Search (DFS).

Het DFS-algoritme is een beetje verschillend voor gerichte en ongerichte grafen, dus die bekijken we apart.

1. Ongerichte grafen.

De knooppunten noemen we Zoon (Z) of Vader (V) waarbij we onthouden welke vader bij welke zoons hoort.
In het begin noemen we alle verbindingslijnen bruikbaar maar in de loop van de zoektocht kunnen die veranderen in onbruikbaar of onderzocht.

De zoekmethode werkt als volgt:

Kies een willekeurig beginknooppunt en geef het nummer 1 .

Kies een willekeurige bruikbare verbindingslijn vanaf dat knooppunt.
Als je bij een knooppunt komt dat al eerder een nummer kreeg is, dan ga je terug en noem je de gebruikte verbindingslijn onbruikbaar en begint weer bij 2.
Als het knooppunt nog geen nummer heeft, dan geeft je het het volgende nummer, en je onthoudt wat de vader was (dat was het knooppunt waar je vandaan kwam).
Maak de verbindingslijn V-Z gericht (van V naar Z) en die verbindingslijn noemen we vanaf nu onderzocht.

Herhaal stap 2 vanaf het nieuwe knooppunt. Net zolang totdat er geen verbindingslijnen meer te vinden zijn.

Als er geen verbindingslijnen meer te vinden zijn, dan ga je terug naar de vader van dit knooppunt en begint vanaf daar weer met stap 2. Als je al bij het beginknooppunt bent (dus als er gaan vader meer is), ben je klaar.

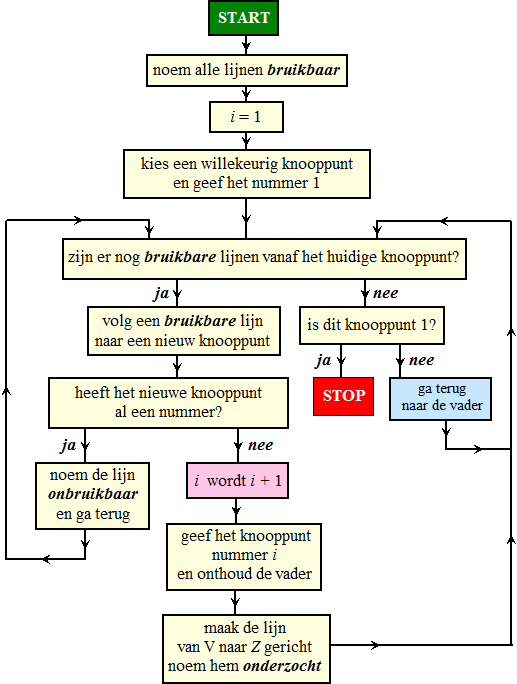
In een stroomdiagram zou dat er zó uitzien:
(bij het paarse blokje gaan we een stapje "dieper" de graaf in, bij het blauwe blokje nemen we een stapje "terug")

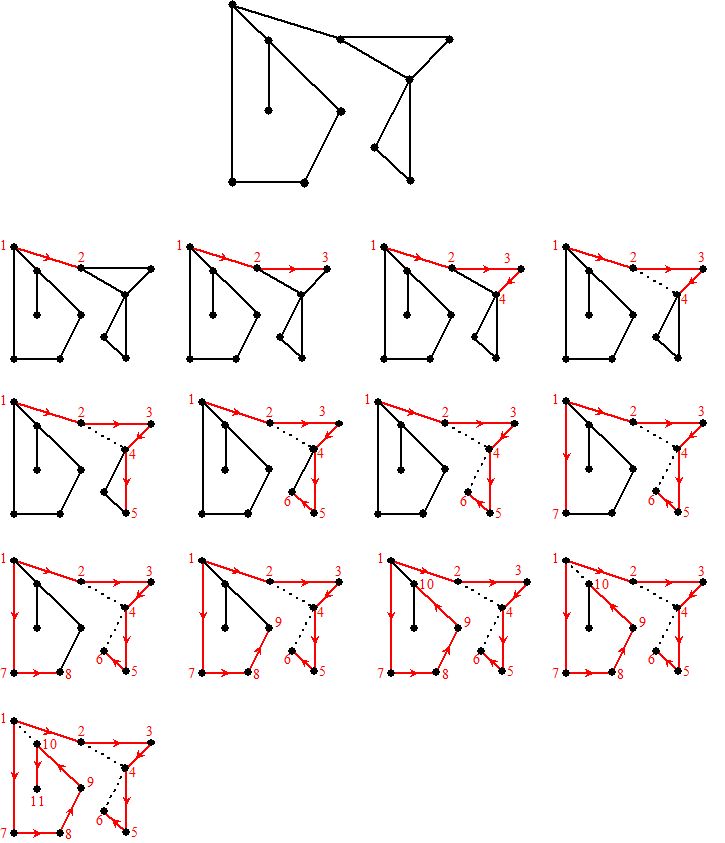
Hieronder zie je in 12 plaatjes het algoritme in werking (leesvolgorde).
Elke keer als een stippellijn verschijnt is een verbindingslijn gekozen die naar een knooppunt leidde dat al een nummer had.
Waarschijnlijk snap je nu ook waarom het Depth-First heet: we gaan eerst zo diep mogelijk de graaf in!

De rode verbindingslijnen leveren uiteindelijk een gerichte graaf met alle knooppunten op, en die wordt wel een DFS-boom van de graaf genoemd. Je ziet dat hij bestaat uit "routes van familieleden". Twee routes in dit geval. Bij het volgen van een route ga je steeds van vader naar zoon.

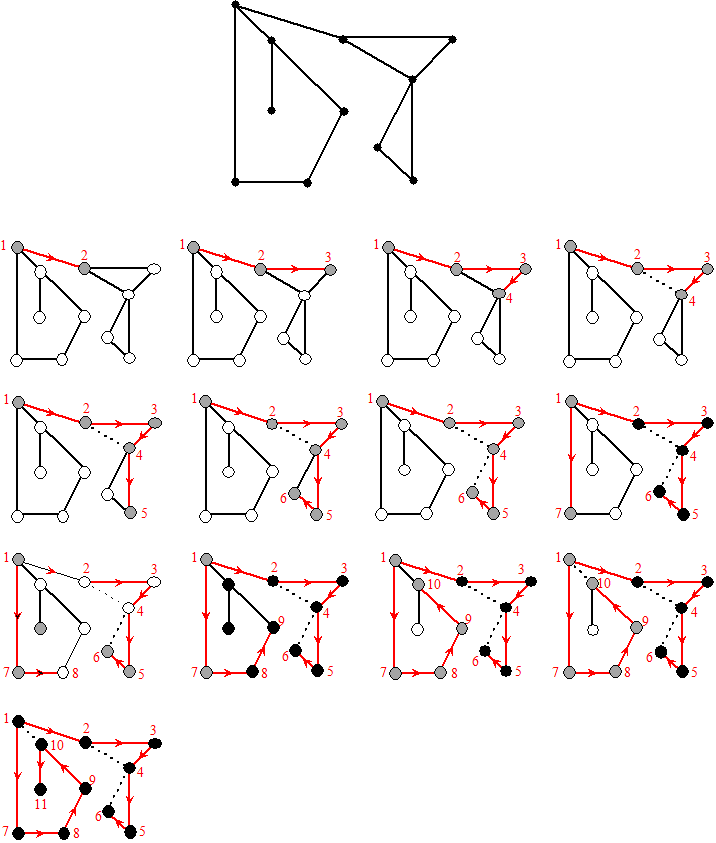
Deze zoekmethode heet ook wel een driekleuren-algoritme: er zijn op elk moment drie soorten knooppunten:
• witte: nog niet bezocht
• grijze: wel bezocht maar nog niet afgesloten
• zwarte: afgesloten.
Dan ziet het er zó uit:

2. Gerichte grafen.

Daarvoor kun je bijna hetzelfde algoritme gebruiken, met één klein verschilletje.

Het kan namelijk gebeuren dat je vanaf een knooppunt geen nieuwe knooppunten meer kunt bereiken, maar dat de graaf toch nog niet "klaar" is.
Kijk maar naar het graafje hiernaast.
Als je aan de linkerkant begint zul je nooit de rechterkant bereiken. Na drie knooppunten wil het niet verder.
In die gevallen moet je gewoon ergens bij een nieuwe willekeurige nog niet bezochte knoop opnieuw beginnen. Ofwel na de STOP uit het stroomdiagram moet je kijken of alle knopen een nummer hebben, en als dat niet zo is er eentje zonder nummer kiezen en doorgaan.

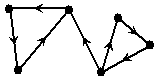In zo'n geval zal het eindresultaat niet uit één boom bestaan maar uit verschillende losse bomen. Dat heeft een bos.

Mooi meegenomen:
Bij grafen die uit verschillende losse componenten bestaan vind je op deze manier meteen hoeveel zulke componenten er zijn (namelijk gewoon door te kijken hoe vaak je "opnieuw" moest beginnen).

Cykels vinden.

Deze DFS-zoektocht levert meteen bij gerichte grafen een mooie manier op om cykels te vinden als die er zijn.
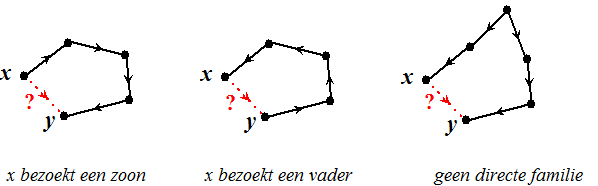
Stel dat de nieuwe lijn die je onderzoekt van knooppunt x naar knooppunt y loopt. Dan zijn er 3 mogelijkheden:

•

y is één van de zonen van x Dan heet de lijn xy een vooruit-lijn (forward-edge).
Het nummer van x is dan kleiner dan dat van y.

•

x is één van de zonen van y. Dan heet lijn xy een terug-lijn (back-edge). Het nummer van y is dan kleiner dan dat van x

•

x en y zijn geen familie van elkaar. Het nummer van y is dan kleiner dan dat van x immers y was al eerder bereikt.
Dat noemen we een kruis-lijn (cross-edge).

En nu hebben we meteen ontdekt of er cykels zijn:

er is een cykel ⇔ er is een terug-lijn geweest bij de DFS

Voorbeeld.

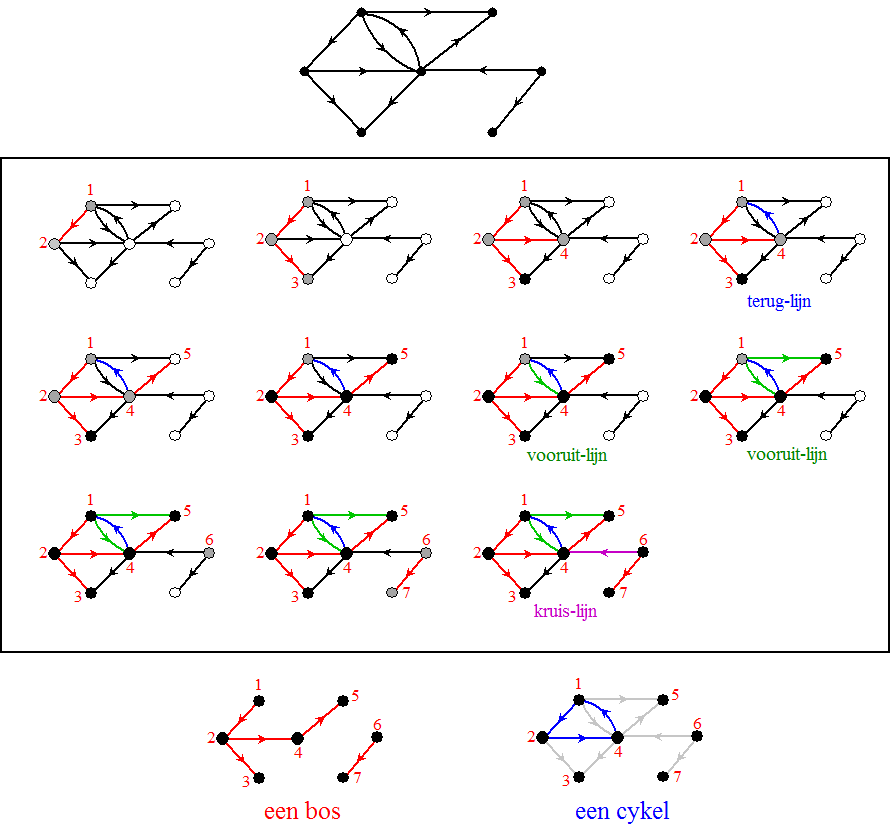
Hieronder zie je een graaf, met daaronder het DFS-algoritme in werking (in leesvolgorde, grijs-wit-zwart zoals hierboven omschreven)
• Rode verbindingslijnen komen in de uiteindelijke boom/bos.
• Blauwe lijnen zijn terug-lijnen en geven cykels.
• Groene lijnen zijn vooruit-lijnen.
• Paarse lijnen zijn kruis-lijnen.

Uiteindelijk levert het een bos (van twee bomen) en een cykel op.

Tuurlijk, ik weet het: die cykel en dat bos had je zó in één oogopslag ook wel gezien. Maar bedenk je steeds dat die algoritmes zijn bedoeld om door een computer uitgevoerd te worden. Vraag je maar eens af of je in een gerichte graaf met zo'n 1000 knooppunten ook zo snel een cykel kunt vinden en kunt zien uit hoeveel bomen het bos bestaat......


OPGAVEN

1.	Je hebt 3 kannen met inhoud 8, 5 en 3 liter. De grootste kan zit vol met 8 liter water, en door water heen en weer te gaan gieten wil je graag die 8 liter verdelen in tweemaal 4 liter. De kannen hebben geen maatstreepjes, dus je moet een kan steeds helemaal leeggieten of helemaal vullen. Geef een "watertoestand" aan met de drie hoeveelheden in de drie kannen (volgorde 8-5-3). De begintoestand is dus (8,0,0), en de eindtoestand moet (4,4,0) worden. 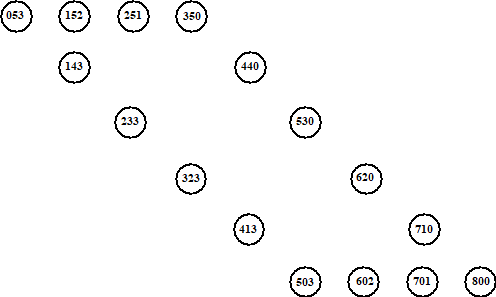Hieronder zie je het begin van een graaf waarin alle mogelijke toestanden als knooppunten staan aangegeven. Verbind in deze graaf de toestanden die in elkaar over kunnen gaan en los daarna met het DFS-algoritme dit gietprobleem op.